Algebra ogólna

Algebra ogólna (algebra uniwersalna lub abstrakcyjna) – obiekt matematyczny będący przedmiotem badań algebry uniwersalnej (zwanej też algebrą ogólną)^[1][2].

Szczególnie ważną klasę algebr stanowią algebry równościowo definiowalne^[3].

Definicje

Definicja 1

Niech ${\displaystyle {\mathfrak {F}}}$ będzie zbiorem i niech ${\displaystyle \varsigma \colon {\mathfrak {F}}\to \mathbb {N} _{0}.}$

Algebrą sygnatury ${\displaystyle \varsigma }$ jest para ${\displaystyle {\mathcal {A}}=\langle A,{\mathcal {J}}\rangle ,}$ gdzie ${\displaystyle A}$ jest zbiorem (zwykle niepustym), a ${\displaystyle {\mathcal {J}}}$ jest funkcją, która elementowi ${\displaystyle {\mathfrak {f}}}$ zbioru ${\displaystyle {\mathfrak {F}}}$ przyporządkowuje ${\displaystyle \varsigma ({\mathfrak {f}})}$-argumentowe działanie ${\displaystyle {\mathcal {J}}({\mathfrak {f}})}$ w zbiorze ${\displaystyle A.}$ Zbiór ${\displaystyle A}$ nazywamy uniwersum algebry ${\displaystyle {\mathcal {A}},}$ funkcję ${\displaystyle {\mathcal {J}}}$ interpretacją zbioru ${\displaystyle {\mathfrak {F}}}$ w algebrze ${\displaystyle {\mathcal {A}}.}$

Dla danej algebry ${\displaystyle {\mathcal {A}},}$ jej uniwersum oznacza się zazwyczaj jako ${\displaystyle |{\mathcal {A}}|.}$ Tak, że zamiast pisać ${\displaystyle {\mathcal {J}}({\mathfrak {f}})}$ pisze się ${\displaystyle {\mathcal {A}}({\mathfrak {f}})}$ albo ${\displaystyle {\mathfrak {f}}^{\mathcal {A}}.}$

Definicja 2

Algebrą^[1] nazywamy zbiór ${\displaystyle {\mathfrak {G}},}$ na którym określony jest skończony lub nieskończony zbiór ${\displaystyle \Omega }$ operacji ${\displaystyle n}$-arnych.

Zbiór symboli operacji ${\displaystyle \Omega ,}$ dla których wskazane są ich arności nazywa się sygnaturą algebry. Jeżeli operacja ${\displaystyle \omega \in \Omega }$ jest ${\displaystyle n}$-arna, to używa się zapisu ${\displaystyle \omega \in \Omega _{n}.}$

Powyższe dwie definicje opisują ten sam obiekt – algebrę ${\displaystyle \omega .}$ W pierwszej definicji zbiór ${\displaystyle {\mathfrak {F}}}$ jest zbiorem nazw (symboli) operacji algebry, ${\displaystyle {\mathcal {J}}}$ jest funkcją przypisującą nazwie operację ${\displaystyle n}$-arną algebry, a funkcja ${\displaystyle \varsigma }$ przypisuje nazwie operacji jej arność.

Definicja 3

Algebrą^[4] (lub algebrą ogólną) nazywamy skończony ciąg postaci:

${\displaystyle \mathbf {A} =(A,a_{1},a_{2},\dots ,a_{m},f_{1},f_{2},\dots ,f_{n}),}$

gdzie:

${\displaystyle A}$ jest niepustym zbiorem zwanym nośnikiem (albo uniwersum algebry),

${\displaystyle a_{1},a_{2},\dots ,a_{m}}$ są pewnymi elementami zbioru ${\displaystyle A}$ (nazywanymi elementami wyróżnionymi),

${\displaystyle f_{1},f_{2},\dots ,f_{n}}$ są działaniami określonymi w zbiorze ${\displaystyle A,}$ przy czym ${\displaystyle f_{i}}$ jest działaniem ${\displaystyle k_{i}}$-argumentowym, tzn. ${\displaystyle f_{i}\colon A^{k_{i}}\to A}$ oraz ${\displaystyle k_{i}>0.}$

Dwie algebry:

${\displaystyle \mathbf {A} =(A,a_{1},a_{2},\dots ,a_{m},f_{1},f_{2},\dots ,f_{n})}$

i

${\displaystyle \mathbf {B} =(B,b_{1},b_{2},\dots ,b_{r},g_{1},g_{2},\dots ,g_{s})}$

nazywamy algebrami podobnymi (lub algebrami tego samego typu) jeśli ${\displaystyle m=r}$ oraz ${\displaystyle n=s,}$ oraz dla każdego ${\displaystyle i\in \{1,2,\dots ,n\}}$ działania ${\displaystyle f_{i}}$ oraz ${\displaystyle g_{i}}$ są działaniami o tej samej liczbie argumentów, tzn. ${\displaystyle f_{i}\colon A^{k_{i}}\to A}$ oraz ${\displaystyle g_{i}\colon B^{k_{i}}\to B.}$

Przykłady algebr

1. Algebra Peana arytmetyki liczb naturalnych, ${\displaystyle {\mathfrak {N}}{:}}$

${\displaystyle \varsigma _{\mathbf {PA} }=\left\langle {\begin{array}{c|c|c|c|c}\mathbf {A} &\mathbf {M} &\mathbf {P} &\mathbf {O} &\mathbf {I} \\\hline 2&2&2&0&0\end{array}}\right\rangle ,}$

${\displaystyle {\mathfrak {N}}(\mathbf {A} )(a,b)=a+b,}$

${\displaystyle {\mathfrak {N}}(\mathbf {M} )(a,b)=a\cdot b,}$

${\displaystyle {\mathfrak {N}}(\mathbf {P} )(a,b)=a^{b},\quad a,b\in \mathbb {N} _{0},}$

${\displaystyle {\mathfrak {N}}(\mathbf {O} )=0,}$

${\displaystyle {\mathfrak {N}}(\mathbf {I} )=1.}$

2. Algebra Presburgera arytmetyki samego dodawania, ${\displaystyle {\mathfrak {N}}^{(+)}{:}}$

${\displaystyle \varsigma _{\mathbf {Pr} }=\left\langle {\begin{array}{c|c|c}\mathbf {A} &\mathbf {O} &\mathbf {I} \\\hline 2&0&0\end{array}}\right\rangle ,}$

${\displaystyle {\mathfrak {N}}^{(+)}(\mathbf {A} )(a,b)=a+b,\quad a,b\in \mathbb {N} _{0},}$

${\displaystyle {\mathfrak {N}}^{(+)}(\mathbf {O} )=0,}$

${\displaystyle {\mathfrak {N}}^{(+)}(\mathbf {I} )=1.}$

3. Algebra Cegielskiego arytmetyki samego mnożenia, ${\displaystyle {\mathfrak {N}}^{(\bullet )}{:}}$

${\displaystyle \varsigma _{\mathbf {Ceg} }=\left\langle {\begin{array}{c|c|c}\mathbf {M} &\mathbf {O} &\mathbf {I} \\\hline 2&0&0\end{array}}\right\rangle ,}$

${\displaystyle {\mathfrak {N}}^{(\bullet )}(\mathbf {A} )(a,b)=a\cdot b,\quad a,b\in \mathbb {N} _{0},}$

${\displaystyle {\mathfrak {N}}^{(\bullet )}(\mathbf {O} )=0,}$

${\displaystyle {\mathfrak {N}}^{(\bullet )}(\mathbf {I} )=1.}$

4. Algebra arytmetyki liczb całkowitych, ${\displaystyle {\mathfrak {Z}}{:}}$

${\displaystyle \varsigma _{\mathfrak {Z}}=\left\langle {\begin{array}{c|c|c|c|c|c}\mathbf {A} &\mathbf {M} &\mathbf {Sb} &\mathbf {N} &\mathbf {O} &\mathbf {I} \\\hline 2&2&2&1&0&0\end{array}}\right\rangle ,}$

${\displaystyle {\mathfrak {Z}}(\mathbf {A} )(a,b)=a+b,}$

${\displaystyle {\mathfrak {Z}}(\mathbf {M} )(a,b)=a\cdot b,}$

${\displaystyle {\mathfrak {Z}}(\mathbf {Sb} )(a,b)=a-b,\quad a,b\in \mathbb {Z} ,}$

${\displaystyle {\mathfrak {Z}}(\mathbf {N} )(a)=-a,\quad a\in \mathbb {Z} ,}$

${\displaystyle {\mathfrak {Z}}(\mathbf {O} )=0,}$

${\displaystyle {\mathfrak {Z}}(\mathbf {I} )=1.}$

5. Algebra podzbiorów zbioru ${\displaystyle X}$, ${\displaystyle {\mathfrak {P}}_{(X)}{:}}$

${\displaystyle \varsigma _{\mathbf {BA} }=\left\langle {\begin{array}{c|c|c|c|c}\mathbf {J} &\mathbf {M} &\mathbf {N} &\mathbf {O} &\mathbf {I} \\\hline 2&2&1&0&0\end{array}}\right\rangle ,}$

${\displaystyle {\mathfrak {P}}_{(X)}(\mathbf {J} )(a,b)=a\cup b,}$

${\displaystyle {\mathfrak {P}}_{(X)}(\mathbf {M} )(a,b)=a\cap b,\quad a,b\in \wp (X),}$

${\displaystyle {\mathfrak {P}}_{(X)}(\mathbf {N} )(a)=X\setminus a,\quad a\in \wp (X),}$

${\displaystyle {\mathfrak {P}}_{(X)}(\mathbf {O} )=\emptyset ,}$

${\displaystyle {\mathfrak {P}}_{(X)}(\mathbf {I} )=X.}$

6. Krata podzielności w ${\displaystyle \mathbb {N} }$, ${\displaystyle {\mathfrak {D}}_{(\mathbb {N} )}{:}}$

${\displaystyle \varsigma _{\mathbf {B\cdot Lat} }=\left\langle {\begin{array}{c|c|c|c}\mathbf {J} &\mathbf {M} &\mathbf {O} &\mathbf {I} \\\hline 2&2&0&0\end{array}}\right\rangle ,}$

${\displaystyle {\mathfrak {D}}_{(\mathbb {N} )}(\mathbf {J} )(a,b)=\mathbf {nwd} \{a,b\},}$

${\displaystyle {\mathfrak {D}}_{(\mathbb {N} )}(\mathbf {M} )(a,b)=\mathbf {nww} ({a,b}),\quad a,b\in \mathbb {N} }$ (zob. nww, nwd)

${\displaystyle {\mathfrak {D}}_{(\mathbb {N} )}(\mathbf {O} )=1,}$

${\displaystyle {\mathfrak {D}}_{(\mathbb {N} )}(\mathbf {I} )=0.}$

Redukty i wzbogacenia

Niech ${\displaystyle {\mathcal {A}}}$ będzie algebrą sygnatury ${\displaystyle \varsigma \colon {\mathfrak {F}}\to \mathbb {N} }$ i niech ${\displaystyle {\mathfrak {F}}_{0}\subseteq {\mathfrak {F}}.}$

Reduktem prostym algebry ${\displaystyle {\mathcal {A}}}$ do ${\displaystyle {\mathfrak {F}}_{0}}$ nazywamy algebrę ${\displaystyle {\mathcal {A}}|_{\mathfrak {F_{0}}}=\langle A,{\mathcal {J}}|_{\mathfrak {F_{0}}}\rangle .}$

Algebra ${\displaystyle {\mathcal {B}}}$ jest wzbogaceniem (prostym) algebry ${\displaystyle {\mathcal {A}},}$ jeśli ${\displaystyle {\mathcal {A}}}$ jest reduktem (prostym) algebry ${\displaystyle {\mathcal {B}}.}$

Przykłady

• ${\displaystyle {\mathfrak {N}}^{(+)}}$ i ${\displaystyle {\mathfrak {N}}^{(\bullet )}}$ są reduktami prostymi ${\displaystyle {\mathfrak {N}}}$
• Algebrę ${\displaystyle {\mathfrak {P}}_{(X)}|_{\{\mathbf {J} ,\mathbf {M} \}}}$ nazywamy kratą podzbiorów zbioru ${\displaystyle X.}$

W niektórych wypadkach wprowadzone wyżej pojęcie reduktu prostego może być niewystarczające. Będzie tak np. w sytuacji, gdy na jednym uniwersum będziemy potrzebowali wprowadzić równolegle kilka struktur wzajemnie ze sobą powiązanych jak jest np. w przypadku pierścieni czy ciał. Wtedy pomocnym okaże się następujące pojęcie reduktu nieprostego:

Redukty nieproste

Niech ${\displaystyle {\mathcal {A}}}$ będzie algebrą sygnatury ${\displaystyle \varsigma \colon {\mathfrak {F}}\to \mathbb {N} }$ i niech ${\displaystyle \pi \colon {\mathfrak {F}}_{0}\to {\mathfrak {F}}}$ będzie różnowartościowe.

Reduktem nieprostym algebry ${\displaystyle {\mathcal {A}}}$ do ${\displaystyle \pi }$ nazywamy algebrę ${\displaystyle {\mathcal {A}}|_{\pi }}$ sygnatury ${\displaystyle \varsigma \circ \pi ,}$ której uniwersum jest ${\displaystyle |{\mathcal {A}}|}$ i w której

${\displaystyle {\mathfrak {f}}^{({\mathcal {A}}|_{\pi })}={\mathcal {A}}{\big (}\pi ({\mathfrak {f}}){\big )},\qquad f\in {\mathfrak {F}}_{0}}$

Przykłady

Pierścień to taka algebra ${\displaystyle {\mathcal {R}}}$ sygnatury ${\displaystyle \varsigma _{\mathbf {ring} }=\left\langle {\begin{array}{c|c|c|c}\mathbf {A} &\mathbf {M} &\mathbf {N} &\mathbf {Z} \\\hline 2&2&1&0\end{array}}\right\rangle ,}$ że redukt ${\displaystyle {\mathcal {R}}|_{\{\mathbf {A} /\mathbf {M} ,\mathbf {N} ,\mathbf {Z} /\mathbf {E} \}}}$ jest grupą przemienną, a ${\displaystyle {\mathcal {R}}|_{\{\mathbf {M} \}}}$ jest półgrupą oraz spełnione są równości:

${\displaystyle x\cdot (y+z)=x\cdot y+x\cdot z\quad {\text{i}}\quad (x+y)\cdot z=x\cdot z+y\cdot z,\quad x,y,z\in |{\mathcal {R}}|.}$

gdzie:

${\displaystyle x+y=\mathbf {A} ^{\mathcal {R}}(x,y),\;x\cdot y=\mathbf {M} ^{\mathcal {R}}(x,y),\;-x=\mathbf {N} ^{\mathcal {R}}(x),\;0=\mathbf {Z} ^{\mathcal {R}},\qquad x,y\in |{\mathcal {R}}|.}$

Tutaj zastosowana jest konwencja notacyjna wedle której ${\displaystyle \{\mathbf {A} /\mathbf {M} ,\mathbf {N} ,\mathbf {Z} /\mathbf {E} \}}$ jest innym zapisem funkcji ${\displaystyle \pi =\left\langle {\begin{array}{c|c|c}\mathbf {M} &\mathbf {N} &\mathbf {E} \\\hline \mathbf {A} &\mathbf {N} &\mathbf {Z} \end{array}}\right\rangle .}$

Ciało to taka algebra ${\displaystyle {\mathcal {F}}}$ sygnatury ${\displaystyle \varsigma _{\mathbf {field} }=\varsigma _{\mathbf {ring} }\cup \{\mathbf {R} \mapsto 1,\mathbf {J} \mapsto 0\},}$ że ${\displaystyle {\mathcal {F}}|_{\{\mathbf {A} ,\mathbf {M} ,\mathbf {N} ,\mathbf {Z} \}}}$ jest pierścieniem, a ${\displaystyle {\mathcal {F}}|_{\{\mathbf {M} ,\mathbf {R} /\mathbf {N} ,\mathbf {J} /\mathbf {E} \}}}$ jest grupą.

Dla wygody przyjmuje się następujące oznaczenia:

${\displaystyle 1=\mathbf {A} ^{\mathcal {F}}(x,y),\;x^{-1}=\mathbf {R} ^{\mathcal {F}}(x),\qquad x\in |{\mathcal {F}}|.}$

Podalgebry

Algebra ${\displaystyle {\mathcal {C}}}$ jest podalgebrą algebry ${\displaystyle {\mathcal {A}},}$ jeśli

1. ${\displaystyle |{\mathcal {C}}|\subseteq |{\mathcal {A}}|}$       oraz
2. ${\displaystyle {\mathcal {C}}({\mathfrak {f}})={\mathcal {A}}({\mathfrak {f}})|_{{\big (}|{\mathcal {C}}|{\big )}^{\varsigma ({\mathfrak {f}})}},{\mathfrak {f}}\in {\mathfrak {F}}.}$

Uwaga 1

Niech ${\displaystyle {\mathcal {A}}}$ będzie algebrą. Na to, aby ${\displaystyle C\subseteq |{\mathcal {A}}|}$ było uniwersum podalgebry algebry ${\displaystyle {\mathcal {A}}}$ potrzeba i wystarcza, aby ${\displaystyle {\mathcal {A}}({\mathfrak {f}})|_{{\big (}|{\mathcal {C}}|{\big )}^{\varsigma ({\mathfrak {f}})}}\subseteq |C|,\qquad {\mathfrak {f}}\in {\mathfrak {F}}}$

Uwaga 2

Niech ${\displaystyle {\mathcal {A}}}$ będzie algebrą i niech ${\displaystyle C\subseteq |{\mathcal {A}}|.}$ Wówczas wśród podalgebr algebry ${\displaystyle {\mathcal {A}},}$ których uniwersum zawiera ${\displaystyle C}$ istnieje algebra najmniejsza.

Algebrę tę nazywamy podalgebrą wyznaczoną przez ${\displaystyle C}$ i oznacza się ${\displaystyle {\mathcal {A}}[C]}$ albo ${\displaystyle \langle C\rangle _{\mathcal {A}}.}$

Przykłady

1. Algebra ${\displaystyle {\mathfrak {N}}|_{\{\mathbf {A} ,\mathbf {M} ,\mathbf {O} ,\mathbf {I} \}}}$ jest podalgebrą algebry ${\displaystyle {\mathfrak {Z}}|_{\{\mathbf {A} ,\mathbf {M} ,\mathbf {O} ,\mathbf {I} \}}.}$
2. Podalgebrą algebry ${\displaystyle {\mathfrak {Z}}|_{\{\mathbf {A} ,\mathbf {M} ,\mathbf {O} ,\mathbf {I} \}}}$ generowaną przez ${\displaystyle \{1\}}$ jest ${\displaystyle {\mathfrak {N}}|_{\{\mathbf {A} ,\mathbf {M} ,\mathbf {O} ,\mathbf {I} \}}.}$
3. Podalgebrą algebry ${\displaystyle {\mathfrak {Z}}}$ generowaną przez ${\displaystyle \{1\}}$ jest ${\displaystyle {\mathfrak {Z}}.}$
4. Uniwersum podalgebry algebry ${\displaystyle {\mathfrak {Z}}|_{\{\mathbf {M} \}}}$ generowanej przez ${\displaystyle \{-1\}}$ jest ${\displaystyle \{-1,1\}.}$
5. Podalgebrą algebry ${\displaystyle {\mathfrak {Z}}|_{\{\mathbf {A} ,\mathbf {M} \}}}$ generowanej przez ${\displaystyle \{-1\}}$ jest ${\displaystyle {\mathfrak {Z}}_{\{\mathbf {A} ,\mathbf {M} \}}.}$

Homomorfizmy

Niech ${\displaystyle {\mathcal {A}}}$ i ${\displaystyle {\mathcal {B}}}$ będą algebrami tej samej sygnatury ${\displaystyle \varsigma \colon {\mathfrak {F}}\to \mathbb {N} _{0}.}$

Funkcja ${\displaystyle h\colon |{\mathcal {A}}|\to |{\mathcal {B}}|}$ jest homomorfizmem algebr ${\displaystyle {\mathcal {A}}}$ i ${\displaystyle {\mathcal {B}},}$ jeśli

${\displaystyle {\mathcal {B}}({\mathfrak {f}}){\big (}h(a_{1}),\dots ,h(a_{\varsigma ({\mathfrak {f}})}){\big )}=h{\big (}{\mathcal {A}}({\mathfrak {f}})(a_{1},\dots ,a_{\varsigma ({\mathfrak {f}})}){\big )},\qquad a_{1},\dots ,a_{\varsigma ({\mathfrak {f}})}\in |{\mathcal {A}}|,\;{\mathfrak {f}}\in {\mathfrak {F}}.}$

Rodzinę wszystkich homomorfizmów z ${\displaystyle {\mathcal {A}}}$ do ${\displaystyle {\mathcal {B}}}$ oznaczamy ${\displaystyle \mathbf {hom} ({\mathcal {A}},{\mathcal {B}}).}$

Homomorfizm różnowartościowy nazywamy monomorfizmem. Rodzinę wszystkich monomorfizmów z ${\displaystyle {\mathcal {A}}}$ do ${\displaystyle {\mathcal {B}}}$ oznaczamy ${\displaystyle \mathbf {mon} ({\mathcal {A}},{\mathcal {B}}).}$

Homomorfizm „na” nazywamy epimorfizmem. Rodzinę wszystkich epoimorfizmów z ${\displaystyle {\mathcal {A}}}$ do ${\displaystyle {\mathcal {B}}}$ oznaczamy ${\displaystyle \mathbf {epi} ({\mathcal {A}},{\mathcal {B}}).}$

Różnowartościowy epimorfizm, to izomorfizm. Rodzinę wszystkich izomorfizmów z ${\displaystyle {\mathcal {A}}}$ do ${\displaystyle {\mathcal {B}}}$ oznaczamy ${\displaystyle \mathbf {iso} ({\mathcal {A}},{\mathcal {B}}).}$

Homomorfizmy algebry w siebie, to endomorfizmy. Izomorfizmy w siebie, to automorfizmy.

Rodzinę wszystkich endomorfizmów algebry ${\displaystyle {\mathcal {A}}}$ oznaczamy ${\displaystyle \mathbf {endo} ({\mathcal {A}}).}$ Rodzinę wszystkich automorfizmów algebry ${\displaystyle {\mathcal {A}}}$ oznaczamy ${\displaystyle \mathbf {aut} ({\mathcal {A}}).}$

Rodzina automorfizmów algebry w siebie tworzy z działaniem składania odwzorowań grupę.

Zauważmy, że algebra ${\displaystyle {\mathcal {A}}}$ jest podalgebrą algebry ${\displaystyle {\mathcal {B}}}$ wtedy i tylko wtedy, gdy ${\displaystyle \mathbf {id} _{|{\mathcal {A}}|}\in \mathbf {hom} ({\mathcal {A}},{\mathcal {B}}).}$

Jeśli ${\displaystyle h\in \mathbf {hom} ({\mathcal {A}},{\mathcal {B}}),}$ to podalgebrę algebry ${\displaystyle {\mathcal {B}}}$ wyznaczoną przez ${\displaystyle h''|{\mathcal {A}}|}$ nazywamy obrazem homomorfizmu ${\displaystyle h}$ i oznaczamy ${\displaystyle \mathbf {im} (h).}$

Przykłady

1. Odwzorowanie ${\displaystyle \mathbb {N} \ni x\mapsto 2x\in \mathbb {Z} }$ jest w ${\displaystyle \mathbf {hom} ({\mathfrak {N}}_{\{\mathbf {O} ,\mathbf {A} \}},\,{\mathfrak {Z}}_{\{\mathbf {O} ,\mathbf {A} \}}),}$
   ale nie jest ani w ${\displaystyle \mathbf {hom} ({\mathfrak {N}}_{\{\mathbf {O} ,\mathbf {I} ,\mathbf {A} \}},\,{\mathfrak {Z}}_{\{\mathbf {O} ,\mathbf {I} ,\mathbf {A} \}}),}$ ani w ${\displaystyle \mathbf {hom} ({\mathfrak {N}}_{\{\mathbf {O} ,\mathbf {M} ,\mathbf {A} \}},\,{\mathfrak {Z}}_{\{\mathbf {O} ,\mathbf {M} ,\mathbf {A} \}}).}$
2. Odwzorowanie ${\displaystyle \mathbb {Z} \ni x\mapsto |x|\in \mathbb {N} }$ jest w ${\displaystyle \mathbf {hom} ({\mathfrak {Z}}_{\{\mathbf {O} ,\mathbf {I} ,\mathbf {M} \}},\,{\mathfrak {N}}_{\{\mathbf {O} ,\mathbf {I} ,\mathbf {M} \}}),}$ ale nie jest w ${\displaystyle \mathbf {hom} ({\mathfrak {Z}}_{\{\mathbf {O} ,\mathbf {I} ,\mathbf {A} \}},\,{\mathfrak {N}}_{\{\mathbf {O} ,\mathbf {I} ,\mathbf {A} \}}).}$
3. Jedynym homomorfizmem ${\displaystyle {\mathfrak {Z}}_{\{\mathbf {O} ,\mathbf {A} ,\mathbf {M} \}}}$ w ${\displaystyle {\mathfrak {N}}_{\{\mathbf {O} ,\mathbf {A} ,\mathbf {M} \}}}$ jest ${\displaystyle h\equiv 0.}$
4. Jedynymi homomorfizmami ${\displaystyle {\mathfrak {N}}_{\{\mathbf {O} ,\mathbf {A} ,\mathbf {M} \}}}$ w ${\displaystyle {\mathfrak {Z}}_{\{\mathbf {O} ,\mathbf {A} ,\mathbf {M} \}}}$ są ${\displaystyle h\equiv 0}$ i ${\displaystyle h\equiv \mathbf {id} _{\mathbb {N} }.}$
5. Jedynym homomorfizmem ${\displaystyle {\mathfrak {N}}_{\{\mathbf {O} ,\mathbf {I} ,\mathbf {A} ,\mathbf {M} \}}}$ w ${\displaystyle {\mathfrak {Z}}_{\{\mathbf {O} ,\mathbf {I} ,\mathbf {A} ,\mathbf {M} \}}}$ jest ${\displaystyle h\equiv \mathbf {id} _{\mathbb {N} }.}$
6. Jedynymi homomorfizmami ${\displaystyle {\mathfrak {N}}_{\{\mathbf {O} ,\mathbf {A} \}}}$ i ${\displaystyle {\mathfrak {Z}}_{\{\mathbf {O} ,\mathbf {A} \}}}$ są postaci ${\displaystyle \mathbb {N} \ni x\mapsto k\cdot x\in \mathbb {Z} ,}$ dla pewnego ${\displaystyle k\in \mathbb {Z} .}$

Kongruencje, zasadnicze twierdzenie algebry

Niech ${\displaystyle {\mathcal {A}}}$ będzie algebrą sygnatury ${\displaystyle \varsigma \colon {\mathfrak {F}}\to \mathbb {N} _{0}.}$

Relacja równoważności ${\displaystyle \approx }$ w ${\displaystyle |{\mathcal {A}}|}$ jest kongruencją algebry, gdy

${\displaystyle a_{1}\approx b_{1},\dots ,a_{\varsigma ({\mathfrak {f}})}\approx b_{\varsigma ({\mathfrak {f}})}\quad \Rightarrow \quad {\mathcal {A}}({\mathfrak {f}})(a_{1},\dots ,a_{\varsigma ({\mathfrak {f}})})\approx {\mathcal {A}}({\mathfrak {f}})(b_{1},\dots ,b_{\varsigma ({\mathfrak {f}})}),}$

${\displaystyle a_{1},\dots ,a_{\varsigma ({\mathfrak {f}})},\;b_{1},\dots ,b_{\varsigma ({\mathfrak {f}})}\in |{\mathcal {A}}|,\;{\mathfrak {f}}\in {\mathfrak {F}}.}$

Przykład

Niech ${\displaystyle h\in \mathbf {hom} ({\mathcal {A}},{\mathcal {B}})}$ i niech

${\displaystyle a\approx _{h}b\quad \Leftrightarrow \quad h(a)=h(b),\qquad a,b\in |{\mathcal {A}}|}$

Wówczas ${\displaystyle \approx _{h}}$ jest kongruencją algebry ${\displaystyle {\mathcal {A}}.}$

Algebra ilorazowa

Niech ${\displaystyle {\mathcal {A}}}$ będzie algebrą sygnatury ${\displaystyle \varsigma \colon {\mathfrak {F}}\to \mathbb {N} _{0}}$ i niech ${\displaystyle \approx }$ będzie kongruencją w ${\displaystyle {\mathcal {A}}.}$

Algebrą ilorazową ${\displaystyle {\mathcal {A}}}$ przez ${\displaystyle \approx }$ jest algebra ${\displaystyle {\mathcal {A}}/\!_{\approx },}$ której uniwersum jest zbiór ilorazowy ${\displaystyle |{\mathcal {A}}|/\!_{\approx }}$ i w której:

${\displaystyle \left({\mathcal {A}}\!/\!_{\approx }\right)({\mathfrak {f}})(a_{1}/\!_{\approx },\dots ,a_{\varsigma ({\mathfrak {f}})}/\!_{\approx })=\left({\mathcal {A}}({\mathfrak {f}})(a_{1},\dots ,a_{\varsigma ({\mathfrak {f}})})\right)\!\!/\!_{\approx },\qquad a_{1},\dots ,a_{\varsigma ({\mathfrak {f}})}\in |{\mathcal {A}}|,\;{\mathfrak {f}}\in {\mathfrak {F}}}$

Przyporządkowanie ${\displaystyle |{\mathcal {A}}|\ni a\mapsto a\!/\!_{\approx }\in |{\mathcal {A}}|/\!_{\approx }}$ nazywamy odwzorowaniem kanonicznym i oznaczamy je symbolem ${\displaystyle \kappa _{\approx }.}$ Jest ono homomorfizmem algebr ${\displaystyle {\mathcal {A}}}$  i  ${\displaystyle {\mathcal {A}}/\!_{\approx }.}$

Zasadnicze twierdzenie algebry

Niech ${\displaystyle h\in \mathbf {hom} ({\mathcal {A}},{\mathcal {B}}),}$ wówczas ${\displaystyle {\mathcal {A}}\!/\!_{\approx _{h}}}$ i ${\displaystyle \mathbf {im} (h)}$ są izomorficzne.

Szczególne algebry

W poniższej sekcji opisano ważne z punktu widzenia matematyki algebry ogólne.

Zbiór

Zbiór to algebra ${\displaystyle {\mathcal {S}}}$ sygnatury ${\displaystyle \varsigma _{\mathbf {set} }=\varnothing .}$

Jest to przypadek zdegenerowany, z punktu widzenia algebry – nieistotny.

Zbiór z wyróżnionym punktem

Zbiór z wyróżnionym punktem to algebra ${\displaystyle {\mathcal {S}}}$ sygnatury ${\displaystyle \varsigma _{\mathbf {set\bullet } }=\{\mathbf {P} \mapsto 0\},}$ gdzie element ${\displaystyle \mathbf {P} ^{\mathcal {S}}}$ nazywa się elementem bądź punktem wyróżnionym algebry ${\displaystyle {\mathcal {S}}.}$

Element ten oznacza się niekiedy symbolem ${\displaystyle \bullet .}$ Zazwyczaj jednak element wyróżniony oznacza się małą literą, która służy do oznaczania uniwersum algebry (czasem z indeksem dolnym ${\displaystyle 0}$).

Algebra unarna

Algebra unarna to algebra ${\displaystyle {\mathcal {U}}}$ sygnatury ${\displaystyle \varsigma _{\mathbf {unalg} }=\{\mathbf {R} \mapsto 1\},}$ gdzie ${\displaystyle \mathbf {R} ^{\mathcal {A}}(x)}$ może mieć wiele różnych oznaczeń w zależności od zastosowań, np. ${\displaystyle \sim \!x,}$ ${\displaystyle \neg x,}$ czy ${\displaystyle -x}$ w notacji prefiksowej, ${\displaystyle x',}$ ${\displaystyle x^{-1}}$ w notacji postfiksowej, czy też ${\displaystyle {\overline {x}}}$ z wykorzystaniem znaków diakrytycznych.

Grupoid

Grupoid to algebra ${\displaystyle {\mathcal {A}}}$ sygnatury ${\displaystyle \varsigma _{\mathbf {grpd} }=\{\mathbf {M} \mapsto 2\},}$ czyli inaczej mówiąc zbiór z działaniem dwuargumentowym.

Zamiast ${\displaystyle {\mathcal {A}}(\mathbf {M} )(x,y)}$ zwykle pisze się ${\displaystyle x\cdot y}$ lub nawet ${\displaystyle xy}$ (tzw. notacja multiplikatywna) lub ${\displaystyle x+y}$ (tzw. notacja addytywna), gdzie ${\displaystyle x,y\in |{\mathcal {A}}|.}$

W notacji multiplikatywnej działanie grupoidu nazywa się mnożeniem, a w notacji addytywnej – dodawaniem. Notacja addytywna używana jest zazwyczaj, gdy działanie grupoidu jest przemienne.

Quasi-grupa

Quasi-grupa to wzbogacenie grupoidu ${\displaystyle {\mathcal {A}}}$ do sygnatury ${\displaystyle \varsigma _{\mathbf {qgrp} }=\varsigma _{\mathbf {grpd} }\cup \{\mathbf {D_{l}} \mapsto 2,\mathbf {D_{r}} \mapsto 2\},}$ w którym spełnione są równości:

${\displaystyle x\cdot (x\backslash y)=y,\;x\backslash (x\cdot y)=y,\;(x/y)\cdot y=x,\;(x\cdot y)/y=x,}$

gdzie:

${\displaystyle x\backslash y:={\mathcal {A}}(\mathbf {D_{l}} )(x,y),\;x/y:={\mathcal {A}}(\mathbf {D_{r}} )(x,y),}$ gdzie ${\displaystyle x,y\in |{\mathcal {A}}|.}$

Działania „${\displaystyle /}$” i „${\displaystyle \backslash }$” nazywa się odpowiednio dzieleniem prawo- i lewostronnym.

Pętla

Pętla to wzbogacenie quasi-grupy ${\displaystyle {\mathcal {A}}}$ do sygnatury ${\displaystyle \varsigma _{\mathbf {qgrp} }\cup \{\mathbf {E} \mapsto 0\},}$ które spełnia równości

${\displaystyle x\cdot \mathbf {e} =\mathbf {e} \cdot x=x,\;x\in |{\mathcal {A}}|,}$

gdzie ${\displaystyle \mathbf {e} ={\mathcal {A}}(\mathbf {E} ).}$

Innymi słowy, pętla to quasi-grupa z elementem neutralnym mnożenia.

Półgrupa

Półgrupa to grupoid z działaniem łącznym.

Monoid

Monoid to wzbogacenie półgrupy ${\displaystyle {\mathcal {A}}}$ do sygnatury ${\displaystyle \varsigma _{\mathbf {mon} }=\varsigma _{\mathbf {grpd} }\cup \{\mathbf {E} \mapsto 0\},}$ które spełnia równości

${\displaystyle x\cdot \mathbf {e} =\mathbf {e} \cdot x=x,\;x\in |{\mathcal {A}}|,}$

gdzie ${\displaystyle \mathbf {e} ={\mathcal {A}}(\mathbf {E} )}$ w notacji multiplikatywnej, często też ${\displaystyle 1={\mathcal {A}}(\mathbf {E} ).}$ W notacji addytywnej zamiast ${\displaystyle {\mathcal {A}}(\mathbf {E} )}$ pisze się zwykle ${\displaystyle 0.}$

Monoid można określić jako półgrupę z elementem neutralnym działania tej półgrupy.

Grupa

Grupa jest wzbogaceniem monoidu ${\displaystyle {\mathcal {A}}}$ do sygnatury ${\displaystyle \varsigma _{\mathbf {mon} }\cup \{\mathbf {R} \mapsto 1\},}$ które spełnia równości

${\displaystyle x\cdot {\mathcal {A}}(\mathbf {R} )(x)={\mathcal {A}}(\mathbf {R} )(x)\cdot x=\mathbf {e} }$ dla ${\displaystyle x\in |{\mathcal {A}}|.}$

Standardowym oznaczeniem ${\displaystyle {\mathcal {A}}(\mathbf {R} )(x)}$ jest ${\displaystyle x^{-1},}$ niekiedy również ${\displaystyle x',}$ w notacji multiplikatywnej; element ten nazywa się wtedy elementem odwrotnym do ${\displaystyle x.}$ W notacji addytywnej element ten oznacza się symbolem ${\displaystyle -x}$ i nazywa elementem przeciwnym do ${\displaystyle x.}$

Grupa to, innymi słowy, monoid z operacją brania elementu odwrotnego/przeciwnego.

Pierścień

Pierścień to algebra ${\displaystyle {\mathcal {R}}}$ sygnatury ${\displaystyle \varsigma _{\mathbf {ring} }=\left\langle {\begin{array}{c|c|c|c}\mathbf {A} &\mathbf {M} &\mathbf {N} &\mathbf {Z} \\\hline 2&2&1&0\end{array}}\right\rangle ,}$ dla której redukt ${\displaystyle {\mathcal {R}}|_{\{\mathbf {A} /\mathbf {M} ,\mathbf {N} /\mathbf {R} ,\mathbf {Z} /\mathbf {E} \}}}$ jest grupą przemienną, a ${\displaystyle {\mathcal {R}}|_{\{\mathbf {M} \}}}$ jest półgrupą oraz spełnione są równości:

${\displaystyle x\cdot (y+z)=x\cdot y+x\cdot z}$ i ${\displaystyle (x+y)\cdot z=x\cdot z+y\cdot z}$ dla ${\displaystyle x,y,z\in |{\mathcal {R}}|,}$

gdzie:

${\displaystyle x+y=\mathbf {A} ^{\mathcal {R}}(x,y),}$

${\displaystyle x\cdot y=\mathbf {M} ^{\mathcal {R}}(x,y),}$

${\displaystyle -x=\mathbf {N} ^{\mathcal {R}}(x),}$

${\displaystyle 0=\mathbf {Z} ^{\mathcal {R}}}$

dla ${\displaystyle x,y\in |{\mathcal {R}}|.}$

Działanie ${\displaystyle \mathbf {A} ^{\mathcal {R}}}$ nazywamy dodawaniem pierścienia, a działanie ${\displaystyle \mathbf {M} ^{\mathcal {R}}}$ jego mnożeniem.

Uwaga

W dowolnym pierścieniu zachodzi ${\displaystyle 0\cdot x=x\cdot 0=0.}$

Ponieważ ${\displaystyle 0\cdot x=(0+0)\cdot x=0\cdot x+0\cdot x,}$ to ${\displaystyle 0\cdot x=0.}$ Podobnie ${\displaystyle x\cdot 0=0.}$

Pierścień, w którym działanie ${\displaystyle \mathbf {M} ^{\mathcal {R}}}$ jest przemienne nazywa się pierścieniem przemiennym.

Pierścień z jedynką

Pierścień z jedynką to algebra ${\displaystyle {\mathcal {R}}}$ sygnatury ${\displaystyle \varsigma _{\mathbf {ring1} }=\varsigma _{\mathbf {ring} }\cup \{\mathbf {J} \mapsto 0\},}$ że ${\displaystyle {\mathcal {R}}_{\{\mathbf {A} ,\mathbf {M} ,\mathbf {N} ,\mathbf {Z} \}}}$ jest pierścieniem, a ${\displaystyle {\mathcal {R}}_{\{\mathbf {M} ,\mathbf {J} /\mathbf {E} \}}}$ jest monoidem.

Element ${\displaystyle \mathbf {J} ^{\mathcal {R}}}$ nazywamy jedynką pierścienia ${\displaystyle {\mathcal {R}}.}$ Oznaczamy go zazwyczaj symbolem ${\displaystyle 1.}$

Pierścień z dzieleniem

Pierścień z dzieleniem to algebra ${\displaystyle {\mathcal {R}}}$ sygnatury ${\displaystyle \varsigma _{\mathbf {ring1} }\cup \{\mathbf {R} \mapsto 1\},}$ że ${\displaystyle {\mathcal {R}}|_{\{\mathbf {A} ,\mathbf {M} ,\mathbf {N} ,\mathbf {Z} \}}}$ jest pierścieniem, a ${\displaystyle {\mathcal {R}}|_{\{\mathbf {M} ,\mathbf {R} ,\mathbf {J} /\mathbf {E} \}}}$ jest grupą.

Dla wygody przyjmuje się oznaczenie:

${\displaystyle x^{-1}=\mathbf {R} ^{\mathcal {R}}(x),}$ gdzie ${\displaystyle x\in |{\mathcal {R}}|.}$

Ciało

Ciało to pierścień z dzieleniem z przemiennym działaniem mnożenia.

Krata

Kratą nazywamy algebrę ${\displaystyle {\mathcal {K}}}$ sygnatury ${\displaystyle \varsigma _{\mathbf {latt} }=\{\mathbf {A} \mapsto 2,\mathbf {K} \mapsto 2\},}$ w której spełnione są równości:

${\displaystyle x\sqcap y=y\sqcap x,\quad x\sqcap (y\sqcap z)=(x\sqcap y)\sqcap z,\quad x\sqcap (x\sqcup y)=x,}$

${\displaystyle x\sqcup y=y\sqcup x,\quad x\sqcup (y\sqcup z)=(x\sqcup y)\sqcup z,\quad x\sqcup (x\sqcap y)=x,}$

gdzie użyto oznaczeń

${\displaystyle x\sqcup y={\mathcal {K}}(\mathbf {A} )(x,y)}$

oraz

${\displaystyle x\sqcap y={\mathcal {K}}(\mathbf {K} )(x,y).}$

Krata rozdzielna to krata spełniająca co najmniej jedną z równości (pozostała równość wynika z przyjętej):

${\displaystyle x\sqcap (y\sqcup z)=(x\sqcap y)\sqcup (x\sqcap z)}$

bądź

${\displaystyle x\sqcup (y\sqcap z)=(x\sqcup y)\sqcap (x\sqcup z).}$

Innym warunkiem, tak koniecznym, jak i dostatecznym, na rozdzielność kraty jest zachodzenie równości:

${\displaystyle (x\sqcap y)\sqcup (y\sqcap z)\sqcup (y\sqcap z)=(x\sqcup y)\sqcap (y\sqcup z)\sqcap (y\sqcup z),}$ gdzie ${\displaystyle x,y,z\in |{\mathcal {K}}|.}$

Krata jest nierozdzielna, gdy zawiera podkratę izomorficzną z jedną z poniższych krat:

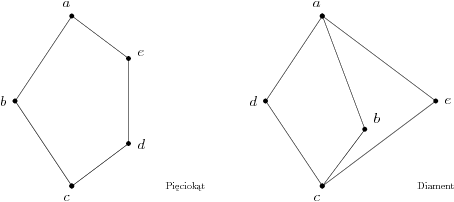
Należy jednak być przezornym, niżej zaprezentowane kraty są rozdzielne:

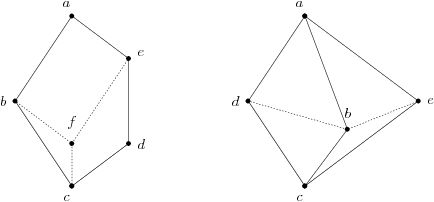
Krata dualna

Redukt ${\displaystyle {\mathcal {K}}^{\mathbf {d} }={\mathcal {K}}|_{\{\mathbf {A} /\mathbf {K} ,\mathbf {K} /\mathbf {A} \}}}$ jest także kratą. Kratę tę nazywamy kratą dualną do ${\displaystyle {\mathcal {K}}.}$ Krata dualna do kraty rozdzielnej jest kratą rozdzielną.

Krata z „zerem”

Krata z „zerem” to wzbogacenie kraty ${\displaystyle {\mathcal {K}}}$ do sygnatury ${\displaystyle \varsigma _{\mathbf {latt\_0} }=\varsigma _{\mathbf {latt} }\cup \{\mathbf {O} \mapsto 0\},}$ w której spełnione są równości:

${\displaystyle x\sqcap \bot =\bot }$ oraz ${\displaystyle x\sqcup \bot =x,}$

gdzie element ${\displaystyle \bot ={\mathcal {K}}(\mathbf {O} )}$ nazywa się spodem lub zerem kraty ${\displaystyle {\mathcal {K}}.}$

Krata z „jedynką”

Krata z „jedynką” to wzbogacenie kraty ${\displaystyle {\mathcal {K}}}$ do sygnatury ${\displaystyle \varsigma _{\mathbf {latt\_1} }=\varsigma _{\mathbf {latt} }\cup \{\mathbf {I} \mapsto 0\},}$ w której spełnione są równości:

${\displaystyle x\sqcap \top =x}$ oraz ${\displaystyle x\sqcup \top =\top ,}$

gdzie element ${\displaystyle \top ={\mathcal {K}}(\mathbf {I} )}$ nazywa się szczytem lub jedynką kraty ${\displaystyle {\mathcal {K}}.}$

Krata ograniczona

Krata ograniczona to wzbogacenie kraty ${\displaystyle {\mathcal {K}}}$ do sygnatury ${\displaystyle \varsigma _{\mathbf {latt\_01} }=\varsigma _{\mathbf {latt} }\cup \{\mathbf {O} \mapsto 0,\mathbf {I} \mapsto 0\},}$ że ${\displaystyle {\mathcal {K}}|_{\{\mathbf {A} ,\mathbf {K} ,\mathbf {O} \}}}$ jest kratą z zerem, a ${\displaystyle {\mathcal {K}}|_{\{\mathbf {A} ,\mathbf {K} ,\mathbf {I} \}}}$ jest kratą z jedynką.

Krata komplementarna

Krata komplementarna to wzbogacenie kraty ograniczonej do sygnatury ${\displaystyle \varsigma _{\mathbf {lcmpl} }=\varsigma _{\mathbf {latt\_01} }\cup \{\mathbf {N} \mapsto 1\},}$ w której spełnione są równości:

${\displaystyle x\sqcap \neg x=\bot }$ oraz ${\displaystyle x\sqcup \neg x=\top ,}$

gdzie ${\displaystyle \neg x={\mathcal {K}}(\mathbf {N} )(x)}$ nazywa się uzupełnieniem elementu ${\displaystyle x}$ w ${\displaystyle {\mathcal {K}}.}$

Komplementarną kratę rozdzielną nazywa się algebrą Boole’a.

Redukt ${\displaystyle {\mathcal {K}}^{\mathbf {d} }={\mathcal {K}}|_{\{\mathbf {A} /\mathbf {K} ,\mathbf {K} /\mathbf {A} ,\mathbf {N} ,\mathbf {O} /\mathbf {I} ,\mathbf {I} /\mathbf {O} \}}}$ jest także algebrą Boole’a. Algebrę tę nazywamy dualizacją algebry ${\displaystyle {\mathcal {K}}.}$

Krata implikacyjna

Relacja ${\displaystyle \leqslant }$ zdefiniowana wzorem

${\displaystyle x\leqslant y\Leftrightarrow x\sqcap y=x}$

definiuje w każdej kracie porządek zwany porządkiem kratowym, w którym operacje ${\displaystyle \sqcap }$ i ${\displaystyle \sqcup }$ są tożsame z operacjami infimum i supremum. Równoważnie porządek ten można zadać wzorem

${\displaystyle x\leqslant y\Leftrightarrow x\sqcup y=y.}$

Krata implikacyjna to wzbogacenie kraty ${\displaystyle {\mathcal {K}}}$ do sygnatury ${\displaystyle \varsigma _{\mathbf {limpl} }=\varsigma _{\mathbf {latt\_1} }\cup \{\mathbf {C} \mapsto 2\},}$ w której zachodzi:

${\displaystyle x\sqcap z\leqslant y\Leftrightarrow z\leqslant x\to y,}$

gdzie element ${\displaystyle x\to y={\mathcal {K}}(\mathbf {C} )(x,y)}$ nosi nazwę relatywnego pseudouzupełnienia elementu ${\displaystyle x}$ względem ${\displaystyle y.}$

W kracie implikacyjnej zachodzi m.in. związek:

${\displaystyle x\to x=\top }$ dla dowolnego ${\displaystyle x\in |{\mathcal {K}}|.}$

Każda krata implikacyjna jest rozdzielna.

Algebra Heytinga

Algebra Heytinga to wzbogacenie kraty implikacyjnej ${\displaystyle {\mathcal {K}}}$ do sygnatury ${\displaystyle \varsigma _{\mathbf {LH} }=\varsigma _{\mathbf {limpl} }\cup \{\mathbf {O} \mapsto 0,\mathbf {N} \mapsto 1\},}$ której redukt ${\displaystyle {\mathcal {K}}|_{\{\mathbf {A} ,\mathbf {K} ,\mathbf {O} \}}}$ jest kratą z zerem i w której zachodzi równość:

${\displaystyle \neg x=x\to \bot ,}$

gdzie ${\displaystyle \neg x=\mathbf {N} ^{\mathcal {K}}(x)}$ dla ${\displaystyle x\in |{\mathcal {K}}|.}$