Algorytm de Casteljau

Algorytm de Casteljau – algorytm opracowany przez Paula de Casteljau, pozwalający na wyznaczenie punktów na wielomianowej krzywej Béziera, czyli obliczanie wartości wielomianów w bazie wielomianów Bernsteina.

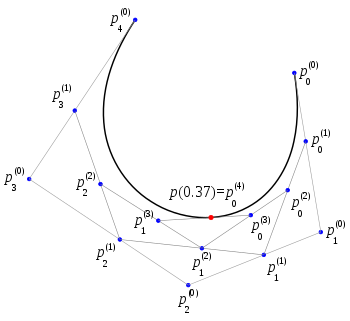
Dana jest dowolna łamana zdefiniowana przez ${\displaystyle n+1}$ wierzchołków ${\displaystyle p_{0},p_{1},\dots ,p_{n}}$ oraz liczba ${\displaystyle t\in [0,1].}$ Każdy odcinek łamanej jest dzielony w stosunku ${\displaystyle t:{1-t},}$ czego wynikiem jest ${\displaystyle n}$ wierzchołków, które wyznaczają nową łamaną. Proces powtarzany jest do chwili, aż zostanie jeden punkt ${\displaystyle p(t),}$ co wymaga wykonania ${\displaystyle n}$ kroków. Ostatecznie otrzymuje się ${\displaystyle n+1}$ ciągów punktów (indeks górny oznacza krok algorytmu):

Punkt ${\displaystyle p(t)^{(n)}}$ leży na krzywej Béziera, której łamaną kontrolną tworzą wyjściowe punkty ${\displaystyle p_{0}^{(0)},p_{1}^{(0)},p_{2}^{(0)},\dots ,p_{n}^{(0)}.}$ Wykonując algorytm dla wszystkich ${\displaystyle t}$ z przedziału ${\displaystyle [0,1]}$ otrzymywane są wszystkie punkty krzywej Béziera.

Algorytm de Casteljau – cztery kolejne łamane, na czerwono wynikowy punkt ${\displaystyle p(t)\ (t=0{,}37).}$ Kolorem czarnym narysowano krzywą Béziera, na której leży ${\displaystyle p(t).}$

Za pomocą algorytmu de Casteljau można również:

• Wyznaczyć punkty kontrolne dwóch krzywych, tak aby połączyć je z zadaną ciągłością geometryczną (zob. krzywa B-sklejana).
• Podzielić krzywą na dwie krzywe w punkcie ${\displaystyle p(t).}$ Łamane kontrolne są wyznaczane przez punkty leżące na brzegach przedstawionego wyżej „trójkąta punktów” – łamaną kontrolną pierwszej krzywej opisują punkty: ${\displaystyle p_{0}^{(0)},p_{0}^{(1)},\dots ,p_{0}^{(n-1)},p_{0}^{(n)},}$ a drugą: ${\displaystyle p_{n}^{(0)},p_{n-1}^{(1)},\dots ,p_{1}^{(n-1)},p_{0}^{(n)}.}$ Obie krzywe są tego samego stopnia co dzielona krzywa.

Podział krzywej Béziera algorytmem de Casteljau

Bibliografia

• Przemysław Kiciak: Podstawy modelowania krzywych i powierzchni: zastosowania w grafice komputerowej. Warszawa: Wydawnictwa Naukowo-Techniczne, 2000. ISBN 83-204-2464-X.
• Michał Jankowski: Elementy grafiki komputerowej. Warszawa: Wydawnictwa Naukowo-Techniczne, 1990, s. 135–138. ISBN 83-204-1326-5.