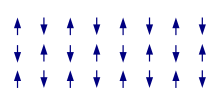
Antyferromagnetyzm

Antyferromagnetyczne ustawienie elementarnych momentów magnetycznych

Antyferromagnetyzm – właściwość magnetyczna materiału; zjawisko polegające na antyrównoległym uporządkowaniu elementarnych momentów magnetycznych w podsieciach sieci krystalicznej^[1]. Typowym przykładem pierwiastka o silnych właściwościach magnetycznych jest mangan. Antyferromagnetyzm występuje np. w CuO (znajdujących się w większości badanych nadprzewodników wysokotemperaturowych), CuMnAs oraz w MnTe.

Antyferromagnetyzm to szczególny przypadek ferrimagnetyzmu. Sieć antyferromagnetyku może być rozpatrywana jako wiele podsieci, z których w każdej momenty magnetyczne mają identyczny kierunek, ale przeciwne zwroty (np. dla antyferromagnetyka II rodzaju o sieci przestrzennie centrowanej (bcc) można wyróżnić 4 różne sieci o uporządkowaniu ferromagnetycznym - czyli dwie prostopadłe do siebie podsieci o uporządkowaniu antyferromagnetycznym). Wypadkowy moment magnetyczny (a zatem i namagnesowanie) całej sieci jest zerowy. Modyfikacja tego uporządkowania może jednak doprowadzić do wytworzenia spontanicznego namagnesowania całej sieci (taki efekt może być spowodowany zanieczyszczeniami lub wzajemnymi nachyleniami spinów, powodującymi, że nie będą równoległe do siebie). Minerały takie nazywamy niedoskonałymi antyferromagnetykami lub antyferrimagnetykami. Przykładem antyferrimagnetyka jest rozpowszechniony w przyrodzie minerał żelaza – hematyt.

Zjawisko antyferromagnetyzmu jest zależne od temperatury. Powyżej temperatury Néela uporządkowanie antyferromagnetyczne ulega zniszczeniu, a substancja przyjmuje właściwości paramagnetyczne. Jest ona inna dla każdego materiału.

Wyprowadzenie temperatury Néela (model Weissa)

Podstawą matematycznego opisu antyferromagnetyka jest rozpatrywanie jego namagnesowania jako sumę namagnesowań podsieci, złożonych z momentów magnetycznych w tym samym kierunku i z tym samym zwrotem. Każde z nich jest źródłem indukcji pola magnetycznego - odpowiednio ${\textstyle {\vec {B}}_{+}}$ oraz ${\textstyle {\vec {B}}_{-}}$ co wyraża się wzorami^[2]:

${\displaystyle {\vec {B}}_{\pm }=-|\lambda |{\vec {M}}_{\pm },}$

gdzie:

• ${\displaystyle \lambda }$ jest stałą pola molekularnego,
• wektor ${\textstyle {\vec {M}}_{\pm }}$ reprezentuje namagnesowanie podsieci.

Dla każdej z podsieci, namagnesowanie dane jest wzorem:

${\displaystyle {M}_{\pm }=M_{S}B_{J}\left(-{\frac {g_{J}\mu _{B}J|\lambda |{M}_{\mp }}{k_{B}T}}\right),}$

gdzie:

• ${\displaystyle M_{S}=ng_{J}\mu _{B}J}$ jest saturacją namagnesowania,
• ${\textstyle B_{J}(y)={\frac {2J+1}{2J}}\coth \left({\frac {2J+1}{2J}}y\right)-{\frac {1}{2J}}\coth \left({\frac {y}{2J}}\right)={\frac {2J+1}{3J}}y+O(y^{3})}$ jest funkcją Brillouina,
• ${\displaystyle g_{J}}$ jest czynnikiem Landego,
• ${\displaystyle \mu _{B}}$ magnetonem Bohra,
• ${\displaystyle J}$ liczbą kwantową całkowitego momentu pędu, ${\displaystyle k_{B}}$ stałą Boltzmana,
• ${\displaystyle T}$ temperaturą.

Skoro namagnesowania podsieci są sobie co do wartości równe, to: ${\displaystyle |M_{+}|=|M_{-}|=M}$, zatem: ${\textstyle {M}=M_{S}B_{J}\left({\frac {g_{J}\mu _{B}J|\lambda |{M}}{k_{B}T}}\right)}$.

W celu rozwiązania tego równania stosujemy układ równań: ${\textstyle {\frac {M}{M_{S}}}=B_{J}(y)~~\wedge ~~y={\frac {g_{J}\mu _{B}J|\lambda |M}{k_{B}T}}}$, który po wykorzystaniu przybliżenia funkcji Brillouina, daje temperaturę graniczną (Néela):

${\displaystyle T_{N}={\frac {g_{J}\mu _{B}(J+1)|\lambda |M_{S}}{3k_{B}}}={\frac {n|\lambda |\mu _{eff}^{2}}{3k_{B}T}}}$,

powyżej której faza antyferromagnetyczna zanika, a materiał staje się paramagnetykiem.

Podatność magnetyczna antyferromagnetyka

Podatność magnetyczna antyferromagnetyków zależy od wielkości zewnętrznego pola magnetycznego oraz od jego kierunku. Przy relacji prostopadłej między wektorem Néela (${\textstyle {\vec {l}}={\vec {M}}_{+}-{\vec {M}}_{-}}$) a indukcją pola magnetycznego ${\textstyle {\vec {B}}}$ (słabe pole), poniżej temperatury Néela podatność magnetyczna jest anizotropowa^[2].

Również poniżej temperatury Néela, dla odpowiedniej wartości pola magnetycznego ustawionego równolegle do wektora Néela następuje spin-flop.

Zobacz też

• ferromagnetyzm
• ferrimagnetyzm
• diamagnetyzm
• paramagnetyzm
• antyferroelektryki

Przypisy

Bibliografia

• Tadeusz Magiera: Wykorzystanie magnetometrii do oceny zanieczyszczenia gleb i osadów jeziornych, Instytut Podstaw Inżynierii Środowiska PAN, Zabrze 2004 (ISBN 83-913824-8-6; PL ISSN 0208-4112)