Asymptota
Asymptota krzywej (gr. ἀσύμπτοτη, „nie stykać się”) – prosta jest asymptotą danej krzywej (w szczególności wykresu funkcji), jeśli dla punktu oddalającego się nieograniczenie wzdłuż krzywej odległość tego punktu od prostej dąży do zera[1].
Asymptota funkcji to asymptota krzywej stanowiącej wykres funkcji.
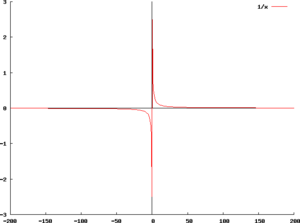
Jeśli krzywa dana jest w postaci gdzie jest funkcją, która nie jest określona w punkcie to ma ona w tym punkcie asymptotę pionową, jeżeli istnieje granica niewłaściwa:
- (asymptota lewostronna)
- (asymptota prawostronna)
- (asymptota obustronna; w szczególności jedna granica może być równa a druga )
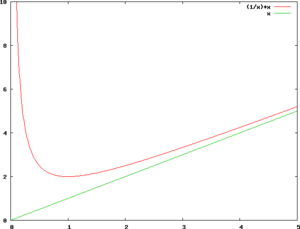
Parametry asymptoty poziomej i ukośnej dla krzywej danej w postaci można wyznaczyć jako granice:
- w przypadku asymptoty prawostronnej:
- oraz
- w przypadku asymptoty lewostronnej:
- oraz
Jeśli przynajmniej jedna z granic wyznaczających lub nie istnieje lub jest granicą niewłaściwą, to wykres nie ma odpowiedniej (prawo- lub lewostronnej) asymptoty ukośnej, ani poziomej. Jeśli to wyznaczona asymptota jest pozioma – równoległa do osi odciętych.
Zobacz też
Przypisy
- ↑ Asymptota, [w:] Encyklopedia PWN [online] [dostęp 2021-07-30].
Bibliografia
- Encyklopedia szkolna. Matematyka. Warszawa: WSiP, 1990, s. 14. ISBN 83-02-02551-8.
Media użyte na tej stronie
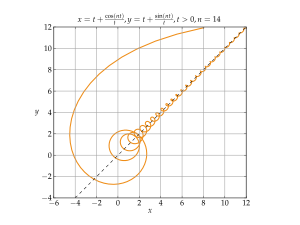
Autor: Guillaume Jacquenot, Licencja: CC BY-SA 3.0
Example of a curve with its asymptote shows that the curve may intersect the asymptote, in this case an infinite amount of times.