Cykl (teoria grafów)
| Ten artykuł należy dopracować |
| Niniejszy artykuł jest częścią cyklu teoria grafów. |
Najważniejsze pojęcia Wybrane klasy grafów Algorytmy grafowe Zagadnienia przedstawiane jako problemy grafowe Inne zagadnienia |
Cykl grafu – ścieżka zamknięta z takim samym ostatnim i pierwszym wierzchołkiem[1]. Dodatkowo ścieżka ta może posiadać wielokrotnie ten sam wierzchołek, również z rzędu – w przypadku tzw. pętli.
Rodzaje cykli
Cykl prosty to droga zamknięta, czyli taka, której koniec (ostatni wierzchołek) jest identyczny z początkiem (pierwszym wierzchołkiem)[2]. Cykl prosty jest szczególnym (prostszym) przypadkiem cyklu.
Cykl Hamiltona – cykl prosty przebiegający przez wszystkie wierzchołki grafu i przechodzący przez nie dokładnie 1 raz (oprócz pierwszego wierzchołka).
Cykl Eulera – cykl zawierający wszystkie krawędzie grafu i przechodzący przez nie dokładnie 1 raz.
Cykl własny – w multigrafie cykl złożony z jednej krawędzi, która zaczyna się i kończy w tym samym wierzchołku (zwany też pętlą własną wierzchołka).
Twierdzenie
- Jeżeli najmniejszy stopień wierzchołka w grafie jest nie mniejszy niż to graf zawiera cykl.
Dowód twierdzenia
Oznaczmy najmniejszy stopień wierzchołka w grafie przez Na podstawie lematu o uściskach dłoni wiemy, że:
Ponieważ każdy wierzchołek grafu (z założenia) jest stopnia co najmniej możemy zapisać, że:
Po przekształceniu otrzymujemy:
Jak widać, liczba krawędzi w grafie jest większa lub równa od liczby wierzchołków Łatwo zauważyć, że wobec tego w grafie występuje przynajmniej jeden cykl, co kończy dowód.
- Wyjaśnienie: stworzenie ścieżki (lub drzewa) o wierzchołkach (niezawierającej cykli) pozwala „zużyć” do połączenia co najwyżej krawędzi. Ostatnia, -ta krawędź, jaką musimy „dołożyć” do grafu zgodnie z założeniami, utworzy cykl.
Przypisy
- ↑ graf, [w:] Encyklopedia PWN [online] [dostęp 2022-03-10].
- ↑ Reinhard Diestel: Graph Theory. Nowy Jork: 2000, s. 7. ISBN 0-387-95014-1.
Media użyte na tej stronie
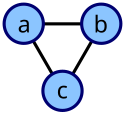
Undirected cyclic graph that can be described by the list {a,b}, {a,c}, {b,c}.