Determinizacja automatu skończonego

Determinizacja automatu skończonego – proces tworzenia deterministycznego automatu skończonego (DAS) z niedeterministycznego automatu skończonego (NAS). Transformacja taka jest zawsze możliwa i otrzymany w jej procesie automat akceptuje dokładnie ten sam język, co automat wejściowy. Jakkolwiek, gdy NAS ma ${\displaystyle n}$ stanów, wynikowy DAS może mieć do ${\displaystyle 2^{n}}$ stanów, wykładniczo więcej, co czyni proces niepraktycznym dla dużych NAS.

Opis metody

Determinizacja niedeterministycznego automatu skończonego ${\displaystyle N}$ polega na konstrukcji deterministycznego automatu ${\displaystyle D,}$ który będzie symulował działanie ${\displaystyle N.}$ Automat ${\displaystyle D}$ po każdym przejściu pamięta zbiór wszystkich stanów, które ${\displaystyle N}$ mógłby osiągnąć w danym kroku. Jeżeli po zakończeniu działania ten zbiór zawiera jakikolwiek stan akceptujący, przeczytane słowo jest akceptowane. Stanami automatu ${\displaystyle D}$ stają się więc zbiory stanów ${\displaystyle N.}$

Formalna konstrukcja

Niech ${\displaystyle N=(Q_{N},f_{N},q_{0},F_{N})}$ nad alfabetem ${\displaystyle \Sigma }$ będzie automatem niedeterministycznym o zbiorze stanów ${\displaystyle Q_{N},}$ funkcji przejść ${\displaystyle f_{N}:\Sigma \to {\mathcal {P}}(Q_{N}),}$ stanie początkowym ${\displaystyle q_{0}}$ i zbiorze stanów akceptujących ${\displaystyle F_{N}.}$ Wtedy automat ${\displaystyle D=(Q_{D},f_{D},\{q_{0}\},F_{D})}$ zdefiniowany w następujący sposób:

• ${\displaystyle Q_{D}={\mathcal {P}}(Q_{N})}$
• ${\displaystyle f_{D}:Q_{D}\times \Sigma \ni (S,a)\to \bigcup _{s\in S}f_{N}(s,a)\in Q_{D}}$
• ${\displaystyle F_{D}=\{S\in Q_{D}:S\cap F_{N}\neq \emptyset \}}$

jest deterministyczny i akceptuje ten sam język co ${\displaystyle N.}$

Przykład

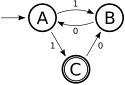
Dany jest NAS:

• S_n={A,B,C}
• ∑_n={0,1}
• s_n=A
• A_n={C}

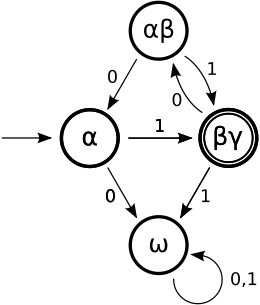
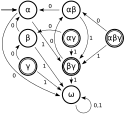
Odpowiadający mu DAS będzie miał 2^|S_n|=2³=8 stanów:

• S_d0={α,β,γ,αβ,αγ,βγ,αβγ,ω}

α odpowiada stanowi A, β stanowi B, a γ stanowi C

stan αβ będzie osiągany na przykład, gdy ze stanu A dla 0 na wejściu odpowiada jednocześnie przejście A→A i A→B, inaczej: A × 0 → {A,B}

stan ω może być osiągnięty gdy dla pewnego stanu nie przewidziano przejścia dla którejś z liter z alfabetu wejściowego

• ∑_d0={0,1}

alfabet wejściowy nie ulega zmianie

• s_d0=α
• A_d0={γ,αγ,βγ,αβγ}

akceptujące są stany w których występuje γ odpowiadająca akceptującemu stanowi C

Ostatni etap polega na usunięciu stanów, których nie można osiągnąć za pomocą żadnej sekwencji liter z alfabetu wejściowego. Należy w tym celu zacząć od stanu początkowego s_d0 i oznaczać kolejne stany do których istnieje ścieżka. Ostatecznie otrzymujemy:

• S_d={α,αβ,βγ,ω}
• ∑_d={0,1}
• s_d=α
• A_d={βγ}

Bibliografia

• John E. Hopcroft: Wprowadzenie do teorii automatów, języków i obliczeń. Warszawa: Wydawnictwo Naukowe PWN, 2005, s. 59. ISBN 83-01-14502-1.