Dodawanie Minkowskiego

Dodawanie Minkowskiego – działanie określone na rodzinie wszystkich (niepustych) podzbiorów danej przestrzeni liniowej ${\displaystyle X}$ wzorem

${\displaystyle A+B=\{a+b\colon a\in A,\;b\in B\}.}$

Powyższa definicja ma sens dla dowolnego zbioru ${\displaystyle X}$ z określonym działaniem ${\displaystyle +}$ (np. ${\displaystyle (X,+)}$ może być grupą, zob. iloczyn kompleksowy), jednakże najczęściej jest ono rozpatrywane w kontekście przestrzeni liniowych. Wynik dodawania Minkowskiego nazywany jest sumą Minkowskiego.

Gdy ${\displaystyle a}$ jest dowolnym elementem przestrzeni ${\displaystyle X}$ oraz ${\displaystyle A}$ jest jej podzbiorem, to stosuje się oznaczenia

${\displaystyle a+B:=\{a\}+B}$ oraz ${\displaystyle A+b:=A+\{b\}.}$

Własności

• Dodawanie Minkowskiego jest łączne, przemienne i rozdzielne względem sumy zbiorów, tzn.

${\displaystyle A+(B\cup C)=(A+B)\cup (A+C)}$

dla dowolnych podzbiorów ${\displaystyle A,B}$ i ${\displaystyle C}$ przestrzeni liniowej ${\displaystyle X}$ (por. modularność).

• Zbiór ${\displaystyle \{0\}}$ jest elementem neutralnym dodawania Minkowskiego.
• Suma Minkowskiego dwóch zbiorów wypukłych jest wypukła.
• Zachodzi następująca nierówność dotycząca mocy sumy Minkowskiego:

${\displaystyle |A+B|\leqslant |A|\cdot |B|.}$

• W przestrzeni liniowo-topologicznej, suma Minkowskiego dwóch zbiorów zwartych jest zbiorem zwartym. Jeżeli ${\displaystyle X}$ jest metryzowalną przestrzenią liniowo-topologiczną, to dodawanie Minkowskiego jest ciągłe względem metryki Hausdorffa w rodzinie zwartych podzbiorów ${\displaystyle X.}$

Nierówność Brunna-Minkowskiego

Jeżeli ${\displaystyle \mu }$ oznacza miarę Lebesgue’a w przestrzeni ${\displaystyle \mathbb {R} ^{n}}$ oraz ${\displaystyle A}$ i ${\displaystyle B}$ są zbiorami wypukłymi w ${\displaystyle \mathbb {R} ^{n},}$ to

${\displaystyle \mu (A+B)^{1/n}\geqslant \mu (A)^{1/n}+\mu (B)^{1/n}}$

Powyższa nierówność nazywana jest nierównością Brunna-Minkowskiego. Nierówność ta jest górnym ograniczeniem objętości sumy dwóch zbiorów mierzalnych w przestrzeni euklidesowej.

Przykład

Dla podzbiorów płaszczyzny

${\displaystyle A=\{(1,0),(0,1),(0,-1)\},}$ ${\displaystyle B=\{(0,0),(1,1),(1,-1)\},}$

ich sumą Minkowskiego jest zbiór

${\displaystyle A+B=\{(1,0),(2,1),(2,-1),(0,1),(1,2),(0,-1),(1,-2)\}.}$

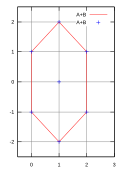
Jeżeli ${\displaystyle A}$ i ${\displaystyle B}$ są trójkątami równoramiennymi (które są wypukłe), to ich sumą Minkowskiego jest sześciokąt wypukły, o którym można powiedzieć, iż powstał z przesuwania ${\displaystyle A}$ wzdłuż krawędzi ${\displaystyle B,}$ jak na rys. 3-4.

• 

  Rys. 1

• 

  Rys. 2

• 

  Rys. 3

Bibliografia

• Rolf Schneider: Convex Bodies: The Brunn-Minkowski Theory. Cambridge University Press, 1993, seria: Encyclopedia of Mathematics and its Applications. ISBN 978-0521352208.