Drzewo (matematyka)

Niniejszy artykuł jest częścią cyklu teoria grafów.

Najważniejsze pojęcia graf drzewo podgraf cykl klika stopień wierzchołka stopień grafu dopełnienie grafu obwód grafu pokrycie wierzchołkowe liczba chromatyczna indeks chromatyczny izomorfizm grafów homeomorfizm grafów więcej... Wybrane klasy grafów graf pełny graf spójny drzewo graf dwudzielny graf regularny graf eulerowski graf hamiltonowski graf planarny więcej... Algorytmy grafowe A* Bellmana-Forda Dijkstry Fleury'ego Floyda-Warshalla Johnsona Kruskala Prima przeszukiwanie grafu – wszerz – w głąb najbliższego sąsiada Zagadnienia przedstawiane jako problemy grafowe problem komiwojażera problem chińskiego listonosza problem marszrutyzacji problem kojarzenia małżeństw Inne zagadnienia kod Graya diagram Hassego kod Prüfera

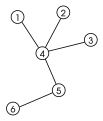
Drzewo – graf nieskierowany, który jest acykliczny i spójny^[1], czyli taki graf, że z każdego wierzchołka drzewa można dotrzeć do każdego innego wierzchołka (spójność) i tylko jednym sposobem (acykliczność, brak możliwości chodzenia „w kółko”)^[2].

Równoważne definicje

Graf prosty G jest drzewem jedynie, jeśli spełnia jeden z warunków^[2]:

• dowolne dwa wierzchołki łączy dokładnie jedna ścieżka prosta
• G jest acykliczny i dodanie krawędzi łączącej dowolne dwa wierzchołki utworzy cykl
• G jest spójny i usunięcie dowolnej krawędzi spowoduje, że G przestanie być spójny

Przykłady drzew

Terminologia

Drzewo, w którym jest wyróżniony jeden z wierzchołków nazywamy drzewem ukorzenionym, a wyróżniony wierzchołek – korzeniem.

Na takim drzewie możemy również określić relacje „rodzinne” pomiędzy wierzchołkami.

Dla dowolnej ścieżki prostej rozpoczynającej się od korzenia i zawierającej wierzchołek v:

• wierzchołki występujące w ścieżce przed v nazywamy jego przodkami v, a wierzchołki występujące po v – potomkami,
• wierzchołek bezpośrednio przed v nazywamy rodzicem lub ojcem, a bezpośrednio po – dzieckiem lub synem,
• wierzchołki mające wspólnego ojca nazywamy braćmi.

Wierzchołki, które nie mają synów nazywamy liśćmi drzewa.

Najdłuższą ścieżkę w drzewie nazywamy średnicą drzewa. Jej długość liczymy stosując programowanie dynamiczne.

W informatyce bardzo często wymaga się, żeby synowie tworzyli nie zbiór, lecz listę uporządkowaną. Taki twór co prawda nie jest matematycznie grafem, jednak ma ogromne znaczenie w tej dziedzinie matematyki.

Graf prosty, acykliczny i niespójny, który można traktować jako zbiór drzew, nazywa się lasem.

Podstawowe operacje na drzewach to:

• wyliczenie wszystkich elementów drzewa,
• wyszukanie konkretnego elementu,
• dodanie nowego elementu w określonym miejscu drzewa,
• usunięcie elementu.

Zastosowanie drzew

Diagramy zależności

W naturalny sposób reprezentują hierarchię danych (obiektów fizycznych i abstrakcyjnych, pojęć itp.) lub zależności typu klient-serwer.

Struktury danych

W informatyce wiele struktur danych jest konkretną realizacją drzewa matematycznego. Wierzchołki drzewa reprezentują konkretne dane (liczby, napisy albo bardziej złożone struktury danych). Odpowiednie ułożenie danych w drzewie może ułatwić i przyspieszyć ich wyszukiwanie. Znaczenie tych struktur jest bardzo duże i ze względu na swoje własności drzewa są stosowane praktycznie w każdej dziedzinie informatyki (np. algorytmika, kryptografia, bazy danych, grafika komputerowa, przetwarzanie tekstu, telekomunikacja).

Specjalne znaczenie w informatyce mają drzewa binarne (liczba dzieci ograniczona do dwóch) i ich różne odmiany, np. drzewa AVL, drzewa czerwono-czarne, BST; drzewa które posiadają więcej niż dwoje dzieci są nazywane drzewami wyższych rzędów.

Zobacz też: Kopiec, Kodowanie Huffmana

Inne

Jako drzewa przedstawia się składnie języków formalnych, w tym rachunku lambda. W teorii gier występują drzewa decyzyjne. Bazy danych i systemy plików stosują wiele algorytmów opartych na drzewach i specjalnych postaciach drzew takich jak drzewa binarne, B drzewa, B+ drzewa, drzewa AVL i inne.

Własności drzew

W grafie ${\displaystyle G=(V,E),}$ gdzie ${\displaystyle V}$ to zbiór wierzchołków grafu, a ${\displaystyle E}$ to zbiór krawędzi. Następujące warunki są równoważne:

1. ${\displaystyle G}$ jest drzewem
2. dla każdych dwóch wierzchołków ${\displaystyle u,v\in V}$ w grafie ${\displaystyle G}$ istnieje dokładnie jedna uv-ścieżka
3. ${\displaystyle G}$ jest spójny i ${\displaystyle |V|=|E|+1}$
4. ${\displaystyle G}$ jest acykliczny i ${\displaystyle |V|=|E|+1}$

W drzewie ukorzenionym istnieje dokładnie jedna ścieżka pomiędzy węzłem a korzeniem. Liczba krawędzi w ścieżce jest nazywana długością (lub głębokością) – liczba o jeden większa określa poziom węzła. Z kolei wysokość drzewa jest równa wysokości jego korzenia, czyli długości najdłuższej ścieżki prostej od korzenia do liścia^[3][4].

Liczba oznaczonych drzew o ${\displaystyle n}$ wierzchołkach wynosi:

${\displaystyle n^{n-2}.}$

Formuła ta nosi nazwę wzoru Cayleya.

Liczba drzew na zbiorze ${\displaystyle n}$-wierzchołków (gdzie ${\displaystyle n}$ jest większe bądź równe 2), z których każdy ma stopień ${\displaystyle d_{1},d_{2},...,d_{n},}$ a suma stopni to ${\displaystyle 2n-2,}$ wynosi:

${\displaystyle {n-2 \choose d_{1}-1,d_{2}-1,\ldots ,d_{n}-1}={\frac {(n-2)!}{(d_{1}-1)!(d_{2}-1)!\cdots (d_{n}-1)!}}.}$

Zobacz też

• drzewo jako struktura danych w informatyce
• drzewo rozpinające
• teoria grafów

Przypisy

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Tree, [w:] MathWorld [online], Wolfram Research [dostęp 2020-12-12]  (ang.).