Elipsa

Elipsa (gr. ἔλλειψις, elleipsis – „brak, opuszczenie, pominięcie”[1][2], zob. geneza) – przypadek ograniczonej krzywej stożkowej, czyli krzywej będącej częścią wspólną powierzchni stożkowej oraz przecinającej ją płaszczyzny. Jest to również miejsce geometryczne wszystkich tych punktów płaszczyzny, dla których suma odległości od dwóch ustalonych punktów jest stałą[3].
Elipsy powstają także jako obrazy okręgu lub sfery w rzucie równoległym i pewnych przypadkach rzutu perspektywicznego. W istocie okręgi są przypadkami szczególnymi elips. Elipsa jest również domkniętym i ograniczonym przypadkiem krzywej stopnia drugiego danej wzorem uwikłanym lub krzywej wymiernej drugiego stopnia. Jest to zarazem najprostsza figura Lissajous powstająca, gdy drgania poziome i pionowe mają tę samą częstotliwość.
Podstawowe pojęcia i własności
Elipsa to gładka krzywa zamknięta symetryczna względem jej środka. Odległość między punktami antypodycznymi elipsy, czyli parami punktów, których środek odcinka przez nie wyznaczany jest zarazem środkiem symetrii elipsy, jest maksymalna i minimalna wzdłuż dwóch prostopadłych kierunków – osi wielkiej (średnicy transwersalnej) oraz osi małej (średnicy sprzężonej).
Półoś wielka, półoś mała, ogniska, kierownice
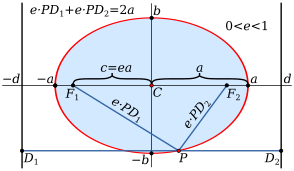
Półoś wielka i półoś mała elipsy (oznaczone na rysunku odpowiednio przez i ) są połowami odpowiednio osi wielkiej i małej. Na osi wielkiej, po obu stronach jej środka, znajdują się dwa wyróżnione punkty oraz takie, że suma odległości dowolnego punktu elipsy od wspomnianych punktów jest stała i równa długości osi wielkiej Każdy z tych dwóch punktów nazywany jest ogniskiem elipsy. Odległości ognisk od środka elipsy są równe:
Jeżeli jest równe to ogniska pokrywają się ze środkiem i wówczas elipsa staje się okręgiem o promieniu
Proste prostopadłe do półosi wielkiej elipsy, odległe od środka elipsy o:
są kierownicami elipsy. Dla okręgu kierownice znajdują się „w nieskończoności”.
Mimośród
Mimośrodem (ekscentrycznością) elipsy nazywamy parametr będący wartością opisującą stosunek długości ogniskowej do długości półosi wielkiej.
Mimośród zawiera się w przedziale od 0 do 1. Jest on równy zeru wtedy i tylko wtedy, gdy a więc kiedy elipsa jest okręgiem. Gdy mimośród dąży do 1, elipsa wydłuża się, a współczynnik dąży do nieskończoności.
Jeżeli elipsa o ogniskach i jest dana równaniem analitycznym
to
Odległość od ogniska do środka nazywana jest mimośrodem liniowym (ekscentrycznością liniową) elipsy.
W obliczeniach geodezyjnych i kartograficznych mają zastosowanie następujące oznaczenia[4]:
mimośród drugi mimośród trzeci mimośród
Parametry te mają zastosowanie do elipsoidy obrotowej, ale wywodzą się z elipsy południkowej.
Spłaszczenie
Podobnie w obliczeniach geodezyjnych i astronomicznych są używane parametry elipsy nazywane spłaszczeniem:
(pierwsze) spłaszczenie Podstawowe, odwrotność 1/f służy do określenia elipsoidy odniesienia. drugie spłaszczenie Rzadziej używane. trzecie spłaszczenie Używane w obliczeniach geodezyjnych.
Geneza nazwy
Nazwa „elipsa” została zaczerpnięta (według Pappusa z Aleksandrii) przez Apoloniusza z Pergi z wczesnej pitagorejskiej terminologii dotyczącej przykładania pól powierzchni: po przyłożeniu prostokąta do odcinka (tj. umieszczeniu podstawy prostokąta wzdłuż odcinka tak, by jeden z końców odcinka i jeden z końców podstawy pokrywały się) przyłożonemu prostokątowi „brakowało” do długości odcinka; równanie elipsy to gdzie skąd a więc kwadrat rzędnej punktu elipsy jest mniejszy niż pole prostokąta o bokach długości równych parametrowi oraz odciętej. Ślad tej relacji można też zaobserwować w równaniu ogólnym stożkowej, w którym elipsa charakteryzuje się spełnianiem nierówności
Kreślenie
Metoda szpilek i sznurka
Elipsę można nakreślić za pomocą dwóch szpilek (pinezek), kawałka sznurka i rysika (ołówka, długopisu):
- Należy wetknąć szpilki w dwa punkty papieru, które staną się ogniskami elipsy, następnie zawiązać sznurek w luźną pętlę wokół szpilek, po czym naciągnąć sznurek za pomocą rysika tak, by powstał trójkąt. Elipsa zostanie nakreślona poprzez przesuwanie rysika po powierzchni kartki przy zachowaniu napięcia sznurka.
Aby nakreślić elipsę wpisaną w dany prostokąt, styczną do jego czterech boków w ich środkach, należy najpierw określić położenie ognisk i długość pętli:
- Niech będą wierzchołkami prostokąta danymi w porządku odwrotnym do wskazówek zegara, gdzie jest jednym z dłuższych boków. Należy nakreślić okrąg o środku w i promieniu równym długości krótszego boku a następnie wyznaczyć styczną do okręgu przechodzącą przez Długość odcinka od do punktu styczności jest odległością między ogniskami. Należy następnie nakreślić dwie proste prostopadłe przez środek prostokąta równoległe do jego boków; będą to osie wielka i mała elipsy. Ogniska rozmieszczone są symetrycznie na osi wielkiej w odległości od środka.
- Aby dostosować długość pętli sznurka należy wetknąć szpilkę w jedno z ognisk, drugą zaś w przeciwny (położony dalej) koniec osi głównej, po czym wykonać ścisłą pętlę wokół dwóch szpilek (tak, by była napięta). Oznacza to, że długość sznurka jest określona wzorem gdzie jest długością ogniskowej[a], a to długość osi wielkiej.
Inne metody
Elipsa może być także nakreślona za pomocą linijki, ekierki oraz rysika:
- Należy nakreślić dwie proste prostopadłe na papierze; będą to osie wielka i mała elipsy. Następnie na linijce należy oznaczyć punkty Obracając jedną ręką linijkę tak, by punkt zawsze leżał na prostej a punkt na prostej i kreśląc rysikiem za pomocą drugiej ręki na papierze, śladem punktu na linijce otrzymuje się elipsę.
Metoda ta może być wykorzystana przy cięciu elips z materiałów drewnianych za pomocą frezarek (ręcznych). Innym przyrządem korzystającym z tej zasady jest elipsograf lub cyrkiel drążkowy: linijka zastąpiona jest prętem z uchwytem na rysik (punkt ) z jednej strony oraz dwoma przesuwnymi bolcami, które przesuwają się w dwóch prostopadłych prowadnicach wyciętych płycie.
Geometria analityczna
Elipsa w pozycji kanonicznej opisana jest w układzie współrzędnych kartezjańskich równaniem
gdzie i są długościami półosi.
Elipsa w postaci parametrycznej dana jest jako
gdzie:
W układzie współrzędnych biegunowych elipsę opisuje wzór
gdzie jest mimośrodem.
Własności
Pole i obwód
Pole powierzchni ograniczonej przez elipsę opisuje wzór
Obwód elipsy jest dany tzw. całką eliptyczną i nie daje się w ogólnym przypadku zapisać w postaci algebraicznej. Przybliżony wzór na obwód elipsy
lepszy
jeszcze lepszy
- gdzie
Dokładny wzór na obwód elipsy wyraża się następująco ( to zupełna całka eliptyczna drugiego rodzaju, a to mimośród elipsy):
- Istnieją różne konwencje zapisu funkcji specjalnej W niektórych argumentem jest nie kwadrat mimośrodu, ale sam mimośród; właściwy wzór pod samym znakiem całki będzie zawierał w drugiej potędze (nigdy w pierwszej czy czwartej).
Chcąc uzyskać długość łuku elipsy, należy skorzystać z niezupełnej całki eliptycznej drugiego rodzaju[5].
Styczna
Styczna w punkcie do elipsy o ogniskach jest dwusieczną kąta zewnętrznego trójkąta Jest to równoznaczne z tym, że promień świetlny wychodzący z jednego ogniska elipsy po odbiciu (zgodnie z zasadą, że kąt padania jest równy kątowi odbicia) od krawędzi elipsy przejdzie przez drugie ognisko (kolorowe kąty na rysunku 1 mają równe miary).
- Dowód
Załóżmy, że dwusieczna tego kąta nie jest styczną, czyli przecina elipsę w pewnym punkcie różnym od
Niech będzie odbiciem w dwusiecznej. Z symetrii wynika, że
- więc
gdzie oznacza długość dużej półosi elipsy. Podobnie pokazujemy, że
Ponieważ kąt jest kątem zewnętrznym trójkąta to punkty są współliniowe, więc są niewspółliniowe.
Stąd Jest to sprzeczne z
Zakładając nieprawdziwość tezy, doszliśmy do sprzeczności, zatem teza została udowodniona.
Dwie styczne
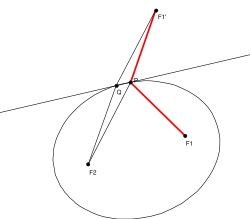
Gdy z punktu leżącego na zewnątrz elipsy poprowadzimy dwie proste, styczne do elipsy w punktach i to
(kąty o tych samych kolorach na rysunku 2 mają równe miary).
- Dowód pierwszej równości
Odbijamy elipsę w obu stycznych. Ogniska obrazów oznaczamy odpowiednio przez
Pamiętając własność stycznej udowodnioną powyżej, łatwo otrzymujemy, że ( – duża półoś). Oprócz tego, bo są obrazami tego samego odcinka.
Zatem
więc
oraz
- gdzie – odbicie w
Lewe części tych równości są równe, oraz, stąd
czyli
Ponieważ
to
Więc mamy a stąd wynika równość którą trzeba było udowodnić.
Trójkąt opisany
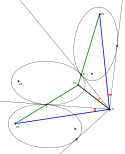
Gdy punkty leżące wewnątrz trójkąta spełniają
to istnieje elipsa o ogniskach wpisana w trójkąt, czyli styczna do jego trzech boków (rys. 3). Wtedy zachodzi również Szczególnym przypadkiem takiej elipsy jest elipsa o ogniskach w ortocentrum i środku okręgu opisanego na trójkącie.
- Dowód
Możemy tak dobrać dużą półoś elipsy, żeby była styczna do Z twierdzenia odwrotnego do powyższej własności o dwóch stycznych (które jest oczywistą konsekwencją tej własności) otrzymujemy, że jest ona styczna do pozostałych boków trójkąta, bo zachodzą równości odpowiednich kątów. Korzystając ponownie z własności stycznych, otrzymujemy równość
Dokonując rachunku na kątach, otrzymujemy powyższe równości dla ortocentrum i środka okręgu opisanego, z czego wynika, że istnieje elipsa wpisana w trójkąt o takich ogniskach.
Okrąg opisany
Niech będzie rzutem prostokątnym ogniska elipsy na styczną do niej. Miejscem geometrycznym wszystkich punktów jest okrąg o środku w środku odcinka łączącego ogniska i o promieniu równym dużej półosi elipsy (czerwony okrąg na rys. 4).
- Dowód
Poprowadźmy dwie równoległe styczne do elipsy w punktach Są one symetryczne względem środka elipsy, więc jest równoległobokiem.
Niech będą rzutami prostokątnymi ognisk na styczną w zaś na styczną w Odbijamy w prostej otrzymując punkt
Punkty są symetryczne względem więc
Stąd jest równoległobokiem, czyli
Ale
Więc gdzie – duża półoś (korzystamy z równości wynikających z istnienia odpowiednich równoległoboków).
jest średnicą okręgu opisanego na prostokącie którego środkiem jest więc co należało pokazać.
Elipsa a jej kierownice
Elipsę można zdefiniować przy użyciu jednego z jej ognisk odpowiadającej jemu kierownicy oraz mimośrodu Miejscem geometrycznym punktów, dla których stosunek odległości od ogniska do odległości od kierownicy jest stały i równy jest elipsa o ognisku kierownicy i mimośrodzie Rozważanym miejscem geometrycznym dla mimośrodu równego 1 jest parabola, zaś dla mimośrodu większego niż jeden jest hiperbola.
Uogólnienia
Elipsa jest szczególnym przypadkiem superelipsy. Odpowiednikiem elipsy w przestrzeni trójwymiarowej jest elipsoida.
Zobacz też
Uwagi
- ↑ Tak nazywa się czasem odległość między ogniskami.
Przypisy
- ↑ Władysław Kopaliński: elipsa; elipsoida; eliptyczny. W: Słownik wyrazów obcych i zwrotów obcojęzycznych [on-line]. [dostęp 2018-07-16]. [zarchiwizowane z tego adresu (2013-07-02)].
- ↑ Henry George Liddell, Robert Scott: ἔλλειψις (ang.). W: A Greek-English Lexicon [on-line]. [dostęp 2018-07-16].
- ↑ Elipsa, [w:] Encyklopedia PWN [online] [dostęp 2021-07-30].
- ↑ dr inż. Paweł Pędzich: Kartografia matematyczna. Zakład Kartografii Politechniki Warszawskiej. [dostęp 2014-03-06]. [zarchiwizowane z tego adresu (2014-03-07)].
- ↑ Dokładniejsze informacje można znaleźć na stronie Wolfram MathWorld o elipsie.
Linki zewnętrzne
- Eric W. Weisstein, Ellipse, [w:] MathWorld [online], Wolfram Research [dostęp 2020-12-12] (ang.).
- Grant Sanderson, Why slicing a cone gives an ellipse, 3blue1brown, YouTube, 1 sierpnia 2018 [dostęp 2021-03-14].
Media użyte na tej stronie
Autor:
- Original work: Inductiveload
- small modification: Wojciech Słota
See: Ellipse_Properties.svg
K and L are tangency points of lines SL or SK and elipse. Angles in the same colour are equal.
If F1, F2 are such points in a triangle so that angles in the same colour are equal, we can inscribe in the triangle an elipse with focuses in F1 and F2.
Autor: MatFizka, Licencja: CC BY 1.0
Proof of a property of elipse tangents. Angles and segments with the same colour are equal. Orange angle is equal to red angles.
Autor: MatFizka, Licencja: CC BY 3.0
Proof of property shown in Elipse_circle.svg. Segments with the same colour are equal and parallel. Orange segments are equal to the major axis of the elipse. One of them is a diameter of the circle from Elipse_circle.svg.
k is a tangent of elipse and P is the tangency point. The tangent is bisector of exterior angle in triangle F1F2P (green and red angles are equal).
X is the ortogonal projection of F1 on a line tangent to the elipse. All posible X-points lie on the red circle with center in point S.