Epicykloida

Epicykloida – krzywa, jaką zakreśla ustalony punkt okręgu toczącego się bez poślizgu na zewnątrz innego, nieruchomego okręgu^[1]. Epicykloida jest szczególnym przypadkiem epitrochoidy.

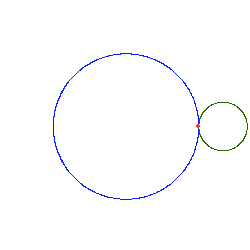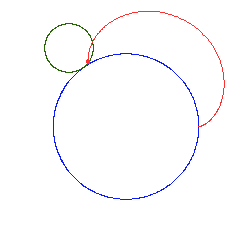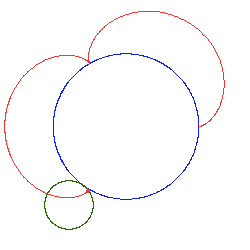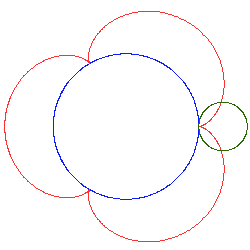
Kształt epicykloidy zależy od stosunku ${\displaystyle {\tfrac {R}{r}}}$ promieni okręgów, nieruchomego do toczącego się. Gdy promienie są równe otrzymuje się krzywą sercową, z grecka zwaną kardioidą (sercowata od gr. καρδιά – serce).

Opis matematyczny

Epicykloidę najłatwiej opisać równaniami parametrycznymi:

${\displaystyle x=(R+r)\cos(t)-r\cos \left({\frac {R+r}{r}}t\right),}$

${\displaystyle y=(R+r)\sin(t)-r\sin \left({\frac {R+r}{r}}t\right).}$

Przykłady

Poniższe rysunki pokazują kilka epicykloid dla różnych wartości ilorazów ${\displaystyle {\tfrac {R}{r}}.}$

• powstawanie kardioidy i kardioida statycznie:

• epicykloida ${\displaystyle {\tfrac {R}{r}}=2}$ (zwana też nefroidą) – powstawanie i krzywa statycznie:

(c) WojciechSwiderski, CC-BY-SA-3.0

• epicykloida ${\displaystyle {\frac {R}{r}}=3}$ – powstawanie i krzywa statycznie:

(c) WojciechSwiderski, CC-BY-SA-3.0

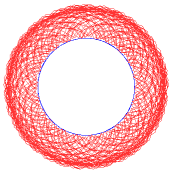
Jeżeli stosunek ${\displaystyle {\frac {R}{r}}}$ jest liczbą niewymierną, otrzymuje się krzywą otwartą. Kolejne przybliżenia takiej sytuacji pokazują poniższe rysunki:

(c) WojciechSwiderski, CC-BY-SA-3.0

Zobacz też

• cykloida
• epicentrum
• hipocykloida

Przypisy

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Epicycloid, [w:] MathWorld [online], Wolfram Research [dostęp 2020-12-13]  (ang.).