Epitrochoida

(c) Sam Derbyshire at the English Wikipedia, CC-BY-SA-3.0

Epitrochoida dla R = 3, r = 1 oraz h = 1/2

Epitrochoida dla R = 3, r = 1 oraz h = 1

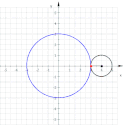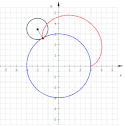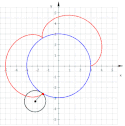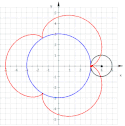
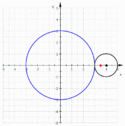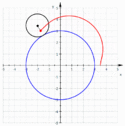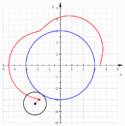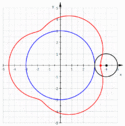
Epitrochoida – krzywa zakreślona przez punkt pozostający w stałym położeniu względem koła toczącego się po pewnym nieruchomym okręgu.

Epitrochoidę najłatwiej opisać równaniami parametrycznymi:

${\displaystyle x=(R+r)\cos t-h\cos \left({\frac {R+r}{r}}t\right),}$

${\displaystyle y=(R+r)\sin t-h\sin \left({\frac {R+r}{r}}t\right),}$

gdzie:

${\displaystyle R}$ – promień nieruchomego okręgu,

${\displaystyle r}$ – promień toczącego się koła,

${\displaystyle h}$ – odległość punktu od środka koła o promieniu ${\displaystyle r.}$

Wzajemna zależność promienia ${\displaystyle r}$ koła i odległości ${\displaystyle h}$ punktu opisującego krzywą od środka tego koła, pozwala na otrzymanie:

• dla ${\displaystyle h=r}$ krzywej przyjmującej postać epicykloidy,
• dla ${\displaystyle h>r}$ krzywej nazywanej również epicykloidą wydłużoną,
• dla ${\displaystyle h<r}$ krzywej nazywanej również epicykloidą skróconą.

Jeżeli stosunek ${\displaystyle {\tfrac {R}{r}}}$ jest liczbą niewymierną, otrzymuje się krzywą otwartą.

Ciekawym zastosowaniem praktycznym epitrochoidy w technice jest cylinder silnika Wankla.

Zobacz też

• cykloida
• hipotrochoida
• lista krzywych
• spirograf

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Epitrochoid, [w:] MathWorld [online], Wolfram Research [dostęp 2020-12-12]  (ang.).
• Strona generująca epitrochoidy z wybranymi parametrami