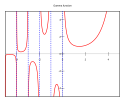
Funkcja Γ

Ten artykuł od 2017-03 wymaga zweryfikowania podanych informacji. Należy podać wiarygodne źródła, najlepiej w formie przypisów bibliograficznych. Część lub nawet wszystkie informacje w artykule mogą być nieprawdziwe. Jako pozbawione źródeł mogą zostać zakwestionowane i usunięte. Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tego artykułu. Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tego artykułu.

Wykres funkcji gamma

Funkcja gamma (zwana też gammą Eulera) – funkcja specjalna, która rozszerza pojęcie silni^[1] na zbiór liczb rzeczywistych i zespolonych. Gdy część rzeczywista liczby zespolonej z jest dodatnia, to całka (całka Eulera):

${\displaystyle \Gamma (z)=\int \limits _{0}^{+\infty }t^{z-1}\,e^{-t}\,dt}$

jest zbieżna bezwzględnie. Całkując przez części, można pokazać, że:

${\displaystyle \Gamma (z+1)=z\cdot \Gamma (z).}$

Zważywszy na to, iż Γ(1)=1, z powyższego wzoru wynika, że Γ(n+1)=n! dla wszystkich liczb naturalnych n.

Drugim sposobem określenia funkcji Γ (dla dowolnych liczb zespolonych) jest:

${\displaystyle \Gamma (z)=\lim _{n\rightarrow +\infty }{\frac {n!n^{z}}{z(z+1)(z+2)\ldots (z+n)}}={\frac {1}{z}}\prod _{n=1}^{\infty }{\frac {\left(1+{\frac {1}{n}}\right)^{z}}{1+{\frac {z}{n}}}}.}$

Możemy także określić odwrotność funkcji Gamma następująco (γ to stała Eulera-Mascheroniego):

${\displaystyle {\frac {1}{\Gamma (z)}}=ze^{\gamma z}\prod _{n=1}^{\infty }\left[\left(1+{\frac {z}{n}}\right)e^{-{\frac {z}{n}}}\right].}$

Funkcja gamma nie ma miejsc zerowych.

Jest nieciągła w każdym punkcie całkowitym niedodatnim, przyjmując w tych punktach za granice lewostronne i prawostronne przeciwne nieskończoności.

Własności funkcji Gamma

${\displaystyle \Gamma (z+1)=z\cdot \Gamma (z)}$

${\displaystyle \Gamma (z)\cdot \Gamma \left(z+{\frac {1}{2}}\right)={\frac {\sqrt {\pi }}{2^{2\cdot z\ -1}}}\cdot \Gamma (2z)}$

Następujące dwa wzory zachodzą, jeśli mianownik jest niezerowy:

${\displaystyle \Gamma (z)\cdot \Gamma (1-z)={\frac {\pi }{\sin {\pi z}}},}$

${\displaystyle \Gamma \left(z+{\frac {1}{2}}\right)\cdot \Gamma \left({\frac {1}{2}}-z\right)={\frac {\pi }{\cos {\pi z}}}.}$

Jeśli ${\displaystyle -1<\operatorname {Re} (z)<1,}$ to:

${\displaystyle \Gamma (z)={\frac {1}{\sin {{\frac {\pi }{2}}z}}}\int _{0}^{\infty }t^{z-1}\sin {t}dt.}$

Jeśli ${\displaystyle 0<\operatorname {Re} (z)<1,}$ to:

${\displaystyle \Gamma (z)={\frac {1}{\cos {{\frac {\pi }{2}}z}}}\int _{0}^{\infty }t^{z-1}\cos {t}dt.}$

Wzór iloczynowy Gaussa:

${\displaystyle \Gamma (nz)={\frac {n^{nz}}{\sqrt {(2\pi )^{n-1}}}}\cdot \Gamma (z)\cdot \Gamma \left(z+{\frac {1}{n}}\right)\cdot \Gamma \left(z+{\frac {2}{n}}\right)\cdot \ldots \cdot \Gamma \left(z+{\frac {n-1}{n}}\right).}$

Dla n całkowitych, dodatnich zachodzi:

${\displaystyle \Gamma (n)\ =\ (n-1)!,}$

${\displaystyle \Gamma \left(n+{\frac {1}{2}}\right)={\frac {(2n-1)!!}{2^{n}}}{\sqrt {\pi }},}$

${\displaystyle \Gamma (n+1/p)=\Gamma (1/p){\frac {(pn-(p-1))!^{(p)}}{p^{n}}},}$

gdzie ${\displaystyle x!^{(p)}}$ oznacza tzw. silnię wielokrotną p-tą.

Wykres funkcji zespolonej

Technika kolorowania dziedziny

Kompletny wykres

Moduł

Argument

Część rzeczywista

Część urojona

Wykres funkcji zespolonej ${\displaystyle \Gamma (z)}$ uzyskany techniką kolorowania dziedziny

Rzut przestrzenny modułu kolorowany argumentem

Oś x – część rzeczywista, oś y – część urojona, oś z – moduł wyniku, kolor – argument wyniku

Wybrane wartości funkcji Gamma

${\displaystyle {\begin{array}{lll}\Gamma (-2)&-&\\\Gamma (-3/2)&={\frac {4{\sqrt {\pi }}}{3}}&\approx 2{,}363271801\\\Gamma (-1)&-&\\\Gamma (-1/2)&=-2{\sqrt {\pi }}&\approx -3{,}544907702\\\Gamma (0)&-&\\\Gamma (1/7)&&\approx 6{,}548062940\\\Gamma (1/6)&&\approx 5{,}566316002\\\Gamma (1/5)&&\approx 4{,}590843712\\\Gamma (1/4)&&\approx 3{,}625609908\\\Gamma (1/3)&&\approx 2{,}678938535\\\Gamma (1/2)&={\sqrt {\pi }}&\approx 1{,}772453851\\\Gamma (1)&=0!&=1\\\Gamma (x_{min})&&=0{,}885603194\\\Gamma (3/2)&={\frac {\sqrt {\pi }}{2}}&\approx 0{,}886226925\\\Gamma (2)&=1!&=1\\\Gamma (5/2)&={\frac {3{\sqrt {\pi }}}{4}}&\approx 1{,}329340388\\\Gamma (3)&=2!&=2\\\Gamma (7/2)&={\frac {15{\sqrt {\pi }}}{8}}&\approx 3{,}323350970\\\Gamma (4)&=3!&=6\\\end{array}}}$

${\displaystyle x_{min}}$ jest to taki argument funkcji Γ, gdzie przyjmuje ona minimum lokalne dla x > 0, ${\displaystyle x_{min}\approx 1{,}461632145.}$

Funkcja Γ(z) nie jest określona dla z = 0, -1, -2, ... (ma tam bieguny o residuum ${\displaystyle (-1)^{n}/n!}$).

Logarytmiczna pochodna funkcji gamma

Wykres logarytmicznej pochodnej funkcji gamma

Można zdefiniować funkcję ${\displaystyle \psi (z),}$ którą nazywamy logarytmiczną pochodną funkcji gamma albo funkcją digamma:

${\displaystyle \psi (z)={\frac {\Gamma '(z)}{\Gamma (z)}},}$

gdzie ${\displaystyle z\neq 0,-1,-2,\dots }$ Zachodzą relacje (${\displaystyle \gamma }$ – stała Eulera-Mascheroniego):

${\displaystyle \psi (z)=-\gamma +\sum _{n=0}^{\infty }\left({\frac {1}{n+1}}-{\frac {1}{n+z}}\right),}$

${\displaystyle \psi '(z)=\sum _{k=0}^{\infty }{\frac {1}{\left(z+k\right)^{2}}}.}$

Ponadto dla dużych x można używać przybliżenia:

${\displaystyle \psi (x)\approx \ln x-{\frac {1}{2x}}.}$

Funkcja poligamma

Definiuje się także funkcję:

${\displaystyle \psi ^{(n)}(z)={\frac {d^{n}\psi (z)}{dz^{n}}}=\left({\frac {d}{dz}}\right)^{n+1}\ln \Gamma (z),}$

którą nazywamy funkcją poligamma n-tego rzędu. Wtedy funkcję digamma można zdefiniować w następujący sposób:

${\displaystyle \psi (z)=\psi ^{(0)}(z).}$

Funkcję ${\displaystyle \psi ^{(1)}}$ nazywa się czasem funkcją trigamma lub trójgamma.

Funkcja ${\displaystyle \ln \Gamma (z)}$ i kilka pierwszych funkcji poligamma na płaszczyźnie zespolonej

${\displaystyle \ln \Gamma (z)}$

${\displaystyle \psi ^{(0)}(z)}$ (digamma)

${\displaystyle \psi ^{(1)}(z)}$ (trigamma)

${\displaystyle \psi ^{(2)}(z)}$

${\displaystyle \psi ^{(3)}(z)}$

${\displaystyle \psi ^{(4)}(z)}$

Wykresy funkcji zespolonej uzyskane techniką kolorowania dziedziny

Wykorzystanie

• Na funkcji gamma opiera się symbol Pochhammera^[2].
• Wzór na objętość n-wymiarowej hipersfery: ${\displaystyle S_{n}=(2*\pi ^{n/2})/(\Gamma (1/2n))}$^[3].

Zobacz też

• funkcja beta

Przypisy

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Gamma Function, [w:] MathWorld [online], Wolfram Research [dostęp 2020-12-12]  (ang.).
• Wykres modułu z funkcji Gamma w zespolonych. mathworks.com. [zarchiwizowane z tego adresu (2009-12-20)].