Funkcja „na”

Zasugerowano, aby zintegrować ten artykuł z artykułem funkcja „w” (dyskusja). Nie opisano powodu propozycji integracji.

Diagram przemienny ilustrujący suriekcję jako funkcję odwracalną prawostronnie

Funkcja „na” (surjekcja^[1], suriekcja^[2][3]) – funkcja przyjmująca jako swoje wartości wszystkie elementy przeciwdziedziny, tj. której obraz jest równy przeciwdziedzinie. Innymi słowy:

• przeciwobraz zbioru niepustego jest niepusty;
• istnieje prawostronna funkcja odwrotna: jeśli f:X→Y, to ∃g: f∘g = id_Y.

Termin suriekcja powstał najpóźniej w 1954 roku, kiedy pojawił się w pracy zespołu Nicolas Bourbaki^[4].

Definicja

Niech ${\displaystyle X}$ oraz ${\displaystyle Y}$ będą dowolnymi zbiorami. Funkcja ${\displaystyle f\colon X\to Y}$ odwzorowuje zbiór ${\displaystyle X}$ na zbiór ${\displaystyle Y}$ wtedy i tylko wtedy, gdy każdy element zbioru ${\displaystyle Y}$ jest wartością funkcji w pewnym punkcie,

${\displaystyle \forall {y\in Y}\;\exists {x\in X}\;f(x)=y,}$

co oznacza się często jako ${\displaystyle f\colon X{\xrightarrow {na}}Y}$ lub ${\displaystyle f\colon X{\xrightarrow[{na}]{\ }}Y.}$

Warunkiem równoważnym jest pokrywanie się przeciwdziedziny z obrazem dziedziny, ${\displaystyle f(X)=Y,}$ inaczej ${\displaystyle \operatorname {Im} f=Y.}$

• 

  Iniekcyjna funkcja niesurjekcyjna (iniekcja, nie bijekcja)

• 

  Iniekcyjna surjekcyjna funkcja (bijekcja)

• 

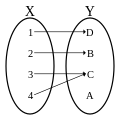
  Nieinjekcyjna surjekcyjna funkcja (surjekcja, nie bijekcja)

• 

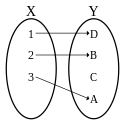
  Nieinjekcyjna niesurjekcyjna funkcja (również nie bijekcja)

Uwaga

Wybór przeciwdziedziny decyduje o surjektywności lub jej braku. Przyjrzyjmy się następującym funkcjom:

${\displaystyle f_{1}\colon \mathbb {R} \to \mathbb {R} }$ określonej wzorem ${\displaystyle f_{1}(x)=x^{2}}$ oraz

${\displaystyle f_{2}\colon \mathbb {R} \to [0,\infty )}$ określonej wzorem ${\displaystyle f_{2}(x)=x^{2}.}$

Tylko druga z powyższych funkcji jest surjekcją, mimo że są one określone tym samym wzorem.

Zauważmy ponadto, że dowolna funkcja jest surjekcją, jeśli jako zbiór ${\displaystyle Y}$ przyjmiemy zbiór jej wartości.

Przykłady

Niech ${\displaystyle x\in \mathbb {R} }$ będzie zmienną rzeczywistą, wówczas poniższe funkcje są suriekcjami:

• ${\displaystyle f\colon x\mapsto x^{a}}$ dla ${\displaystyle a\in \{2n+1\colon n\in \mathbb {N} \}}$ na ${\displaystyle \mathbb {R} }$;
• dowolny wielomian rzeczywisty stopnia nieparzystego, rozpatrywany jako funkcja do zbioru liczb rzeczywistych – wynika to z twierdzenia Darboux o funkcjach ciągłych, do których wielomiany rzeczywiste należą;
• ${\displaystyle f\colon x\mapsto \operatorname {tg} \;x}$ dla ${\displaystyle x\in \bigcup \{(-{\tfrac {\pi }{2}}+k\pi ,{\tfrac {\pi }{2}}+k\pi )\colon k\in \mathbb {Z} \}}$ na ${\displaystyle \mathbb {R} }$;
• ${\displaystyle f\colon \mathbb {R} {\overset {\mathrm {na} }{\mapsto }}\mathbb {Z} ,\quad f(x)=\lceil x\rceil }$;
• ${\displaystyle f\colon \mathbb {R} {\overset {\mathrm {na} }{\mapsto }}\{1\},\quad f(x)=1}$;
• wszelkie bijekcje.

Pisownia

Słowo surjekcja tradycyjnie bywa pisane przez j, tę wersję jako jedyną dopuszczalną podaje słownik języka polskiego PWN^[1]. Zasady pisowni polskiej w ogólnych przypadkach nakazują jednak stosowanie j po innych spółgłoskach niż c, s i z w wypadku, gdy przedrostek jest zakończony spółgłoską, a rdzeń zaczyna się od j; np. podjazd, nadjechał, zjawa czy rozjaśnić. W pozostałych wypadkach pisze się i. Z tego powodu dopuszczalna i przez niektórych stosowana jest pisownia suriekcja i iniekcja przez i. Jest to jednak termin fachowy, pochodzenia obcego, gdzie można stosować inne reguły i matematycy przeważnie używają pisowni surjekcja oraz injekcja przez j. Językoznawcy często uznają uzus obowiązujący wśród specjalistów posługujących się tym pojęciem. Oni zaś stosują obydwie formy, zarówno surjekcja (częściej), jak i suriekcja.

Zobacz też

• epimorfizm
• funkcja różnowartościowa (iniekcja)
• funkcja „w”

Przypisy

Bibliografia

• Marian Gewert, Zbigniew Skoczylas: Analiza matematyczna 1 : definicje, twierdzenia, wzory. Wyd. XI zmienione. Wrocław: Oficyna Wydawnicza GiS, 2001, s. 18. ISBN 83-85941-82-7.