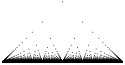
Funkcja Riemanna

Wykres dla przedziału [0,1]

Funkcja Riemanna – funkcja rzeczywista zdefiniowana wzorem:

[1]

W szczególności, dla wszystkich argumentów całkowitych, ponieważ dla każdej liczby całkowitej x nieskracalną postacią ułamka jest

Nazwa pochodzi od nazwiska Bernharda Riemanna, jednak w literaturze posiada wiele nazw.[1]

Własności

  • Ciągłość: Funkcja ta jest ciągła w każdym niewymiernym punkcie swojej dziedziny, i nieciągła w punktach wymiernych.
  • Całkowalność: Funkcja Riemanna jest całkowalna w sensie Riemanna na każdym przedziale domkniętym ponieważ miara zbioru punktów nieciągłości jest równa 0. Ponadto,

Zobacz też

Przypisy

  1. ↑ a b Eric W. Weisstein, Dirichlet Function, [w:] MathWorld [online], Wolfram Research [dostęp 2018-01-27] (ang.).

Media użyte na tej stronie

Thomae function (0,1).svg
Plot of Thomae's function on the interval (0,1). Shown are all rational points with denominator at most 200.

Created using the following Java code: 

public class Thomae {
	
	static int gcd(int a, int b) {
		while(a>0 && b>0) {
			if(a>b) a -= a/b*b;
			else b -= b/a*a;
		}
		return a>0 ? a : b;
	}
	
	public static void main(String[] args) {
		int max = 200;
		
		int width = 1280;
		int height = 660;
		
		int border = 20;
		int x0 = border;
		int x1 = width - border;
		double dx = x1-x0;
		int y0 = height - border;
		double dy = -dx;
		int r=5;
		
		System.out.println("<?xml version=\"1.0\" standalone=\"no\"?>");
		System.out.println("<!DOCTYPE svg PUBLIC \"-//W3C//DTD SVG 1.1//EN\" \"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd\">");
		System.out.println("<svg width=\""+ width +"\" height=\""+ height +"\" xmlns=\"http://www.w3.org/2000/svg\" version=\"1.1\">");
		
		for(int q=1; q<max; q++) for(int p=0; p<q; p++) if(gcd(p, q) == 1) {
			System.out.println("  <circle cx=\""+ (x0+dx*p/q) + "\" cy=\""+ (y0+dy*1/q) +"\" r=\""+ r +"\" fill=\"black\" stroke=\"none\" />");
		}
		
		System.out.println("</svg>");
	}
	
}