Funkcja W Lamberta

Wykres funkcji W₀(x).

(c) Sam Derbyshire z angielskojęzycznej Wikipedii, CC-BY-SA-3.0

z = Re(W₀(x + i y)) (część rzeczywista funkcji)

(c) Sam Derbyshire z angielskojęzycznej Wikipedii, CC-BY-SA-3.0

z = Im(W₀(x + i y)) (część urojona funkcji)

(c) Sam Derbyshire z angielskojęzycznej Wikipedii, CC-BY-SA-3.0

moduł funkcji z = W₀(x + i y)

Funkcja W Lamberta lub funkcja Omega – funkcja specjalna używana podczas rozwiązywania równań zawierających niewiadomą zarówno w podstawie, jak i wykładniku potęgi. Określona jest jako funkcja odwrotna do ${\displaystyle f(z)=ze^{z},}$ gdzie z należy do zbioru liczb zespolonych. Oznacza się ją symbolem ${\displaystyle W(y).}$ Zatem dla każdej liczby zespolonej z zachodzi:

${\displaystyle z=W(z)e^{W(z)}.}$

Ponieważ funkcja f nie jest iniekcją, zatem W(z) musi być odwzorowaniem wielowartościowym. Tworzy się zatem rodzinę funkcji ${\displaystyle W_{k}(z),}$ gdzie ${\displaystyle k\in \mathbb {Z} }$ oznacza numer gałęzi. Dla k=0 przyjmuje się gałąź W₀(z) opisaną poniżej, rozszerzoną na wszystkie liczby zespolone. Ze wzrostem k rośnie też część urojona funkcji W_k(z).

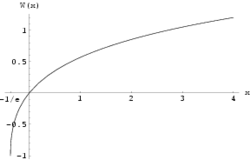
Jeśli założymy, że x oraz W(x) mają być rzeczywiste, wtedy odwzorowanie istnieje jedynie dla x ≥ −1/e, a na odcinku (−1/e,0) jest dwuwartościowe. Jeśli dodatkowo założymy, że W(x) ≥ −1, otrzymamy funkcję W₀(x) przedstawioną na wykresie obok. Alternatywna gałąź oznaczana W₋₁(x) to funkcja malejąca od −1 (dla x = −1/e) do −∞ (dla x = 0⁻).

Własności funkcji W(z)

Równanie ${\displaystyle x^{x}=z}$ ma rozwiązanie:

${\displaystyle x={\frac {\ln(z)}{W(\ln z)}}=\exp W(\ln(z)).}$

Pierwotną funkcji ${\displaystyle W}$ można znaleźć, całkując przez podstawienie: jeżeli ${\displaystyle w=W(x),}$ to ${\displaystyle x=we^{w},}$ wówczas:

${\displaystyle \int W(x)\ dx=x\left(W(x)-1+{\tfrac {1}{W(x)}}\right)+C.}$

Pochodna funkcji ${\displaystyle W}$ wynosi:

${\displaystyle {\frac {dW(z)}{dz}}={\frac {W(z)}{z(1+W(z))}}\quad \mathrm {dla\ } z\neq -{\frac {1}{e}}.}$

Dowód

Różniczkując równanie ${\displaystyle z=W(z)e^{W(z)}}$ obustronnie względem ${\displaystyle z,}$ otrzymamy

${\displaystyle 1=W(z)e^{W(z)}W'(z)+W'(z)e^{W(z)}=W'(z)\left(W(z)e^{W(z)}+e^{W(z)}\right),}$

${\displaystyle W'(z)={\frac {1}{z+e^{W(z)}}}={\frac {W(z)}{W(z)z+W(z)e^{W(z)}}}={\frac {W(z)}{z(W(z)+1)}}.}$

Zastosowanie

Funkcja W znajduje zastosowanie w kombinatoryce i przy rozwiązywaniu trudnych równań różniczkowych. Wiele równań zawierających niewiadomą w potędze może być rozwiązanych za pomocą tej funkcji. Najczęściej problem polega wtedy na sprowadzeniu równania do formy Y = Xe^X, przez co automatycznie otrzymuje się rozwiązanie:

${\displaystyle Y=Xe^{X}\;\Longleftrightarrow \;X=W(Y).}$

Przykład 1

${\displaystyle 2^{t}=5t}$

${\displaystyle \Rightarrow 5t=e^{t\ln 2}}$

${\displaystyle \Rightarrow {\frac {1}{5t}}=e^{-t\ln 2}}$

${\displaystyle \Rightarrow \underbrace {-{\tfrac {\ln 2}{5}}} _{Y}=\underbrace {-t\ln 2} _{X}e^{\overbrace {-t\ln 2} ^{X}}}$

${\displaystyle \Rightarrow \underbrace {-t\ln 2} _{X}=W{\Big (}\underbrace {-{\tfrac {\ln 2}{5}}} _{Y}{\Big )}}$

${\displaystyle \Rightarrow t=-{\frac {W\left(-{\frac {\ln 2}{5}}\right)}{\ln 2}}}$

Przykład 2

Jeśli wartość ${\displaystyle z^{z^{z^{\cdots }}}}$ jest skończona, można ją obliczyć w następujący sposób:

${\displaystyle c=z^{z^{z^{\cdots }}},}$

${\displaystyle \Rightarrow c=z^{c}.}$

Używając rozumowania przedstawionego powyżej, otrzymujemy:

${\displaystyle c=-{\frac {W\left(-\ln z\right)}{\ln z}}.}$

Uwaga

Aby udowodnić, że wartość ${\displaystyle z^{z^{z^{\cdots }}}}$ istnieje, należy rozpatrzyć ciąg:

${\displaystyle a=(z,z^{z},z^{z^{z}},\dots )}$

lub (w postaci rekurencyjnej):

${\displaystyle {\begin{cases}a_{1}=z\\a_{n}=z^{a_{n-1}}\end{cases}}}$

i udowodnić istnienie jego granicy. Jeśli ona istnieje, wtedy zachodzi równość

${\displaystyle \lim \limits _{n\to \infty }a_{n}=c.}$

Przykład 3

Równanie różniczkowe:

${\displaystyle y'(t)=ay(t-1)}$

ma równanie charakterystyczne λ = ae^−λ, czyli λ = W_k(a), gdzie k to numer gałęzi (jeśli a jest rzeczywiste, wtedy wystarczy uwzględnić gałąź W₀(a)). Rozwiązanie wynosi zatem:

${\displaystyle y(t)=e^{W_{k}(a)\,t}.}$

Ważne wartości

${\displaystyle W_{0}(-{\tfrac {\pi }{2}})}$	${\displaystyle ={\tfrac {\pi }{2}}i}$
${\displaystyle W_{0}(-1)}$	${\displaystyle \approx -0{,}31813-1{,}33723i}$
${\displaystyle W_{0}(-{\tfrac {1}{e}})}$	${\displaystyle =-1}$
${\displaystyle W_{0}(-{\tfrac {\ln 2}{2}})}$	${\displaystyle =-\ln 2}$
${\displaystyle W_{0}(0)}$	${\displaystyle =0}$
${\displaystyle W_{0}(e)}$	${\displaystyle =1}$
${\displaystyle W_{0}(1)}$	${\displaystyle =\Omega \approx 0{,}56714329}$ (stała Omega)

Linki zewnętrzne

• KrzysztofK. Oleszkiewicz KrzysztofK., Funkcja Lamberta, [w:] pismo „Delta” [online], deltami.edu.pl, lipiec 2014, ISSN 0137-3005 [dostęp 2022-07-19]  (pol.).