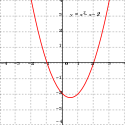
Funkcja kwadratowa

${\displaystyle f(x)=x^{2}-x-2}$

Funkcja kwadratowa – funkcja wielomianowa drugiego stopnia, czyli postaci^[1]:

${\displaystyle f(x)=ax^{2}+bx+c,}$

gdzie ${\displaystyle a,b,c}$ są pewnymi stałymi, przy czym ${\displaystyle a\neq 0}$ (co gwarantuje, że funkcja kwadratowa nie degeneruje się do funkcji liniowej). Funkcja kwadratowa jest wyznaczona przez pewien wielomian drugiego stopnia^[a], dlatego nazywa się ją czasami trójmianem kwadratowym^[2].

Edukacja szkolna obejmuje najczęściej funkcje kwadratowe o rzeczywistej dziedzinie, przeciwdziedzinie oraz współczynnikach, jednak funkcje te można definiować w dowolnym ciele.

Postacie funkcji kwadratowej

Postać ogólna (wielomianowa)

Jest to postać podana w definicji we wstępie^[3]

${\displaystyle f(x)=ax^{2}+bx+c,}$

gdzie ${\displaystyle a,b,c}$ są ustalonymi liczbami rzeczywistymi i ${\displaystyle a\neq 0}$^[3].

Postać kanoniczna

${\displaystyle f(x)=a(x-p)^{2}+q,}$

gdzie:

${\displaystyle p=-{\tfrac {b}{2a}},\quad q=-{\tfrac {\Delta }{4a}},\quad \Delta =b^{2}-4ac.}$^[3]

Wyrażenie ${\displaystyle \Delta }$ nazywa się wyróżnikiem funkcji kwadratowej ${\displaystyle f.}$

Postać kanoniczną można wyprowadzić z postaci ogólnej:

${\displaystyle {\begin{aligned}ax^{2}+bx+c&=ax^{2}+bx+{\tfrac {b^{2}}{4a}}-{\tfrac {b^{2}}{4a}}+c\\&=a\left(x^{2}+2x{\tfrac {b}{2a}}+{\tfrac {b^{2}}{4a^{2}}}\right)-{\tfrac {b^{2}}{4a}}+{\tfrac {4ac}{4a}}\\&=a\left(x+{\tfrac {b}{2a}}\right)^{2}-{\tfrac {b^{2}-4ac}{4a}}.\end{aligned}}}$

Postać kanoniczna ułatwia kreślenie wykresu.

Postać iloczynowa

${\displaystyle f(x)=a\left(x-{\tfrac {-b+{\sqrt {\Delta }}}{2a}}\right)\left(x-{\tfrac {-b-{\sqrt {\Delta }}}{2a}}\right).}$

Przedstawienie takie jest możliwe, o ile tylko wyróżnik ${\displaystyle \Delta }$ jest nieujemny^[3] (istnieje jego rzeczywisty pierwiastek). W dziedzinie zespolonej jest zawsze możliwe – jeżeli ${\displaystyle \Delta <0,}$ to

${\displaystyle {\sqrt {\Delta }}=i{\sqrt {4ac-b^{2}}},}$

gdzie ${\displaystyle i}$ jest jednostką urojoną.

Postać iloczynową można wyprowadzić z postaci kanonicznej, stosując wzór na różnicę kwadratów:

${\displaystyle {\begin{aligned}a(x-p)^{2}+q&=a(x-{\tfrac {-b}{2a}})^{2}-{\tfrac {\Delta }{4a}}\\&=a\left[\left(x-{\tfrac {-b}{2a}}\right)^{2}-{\tfrac {\Delta }{4a^{2}}}\right]\\&=a\left(x-{\tfrac {-b}{2a}}-{\tfrac {\sqrt {\Delta }}{2a}}\right)\left(x-{\tfrac {-b}{2a}}+{\tfrac {\sqrt {\Delta }}{2a}}\right).\end{aligned}}}$

Postać iloczynowa ułatwia odczytanie jej miejsc zerowych (o ile istnieją).

Miejsca zerowe

• ${\displaystyle \Delta >0.}$

Oznaczając

${\displaystyle x_{1}={\tfrac {-b-{\sqrt {\Delta }}}{2a}}\;\;{}}$ oraz ${\displaystyle {}\;\;x_{2}={\tfrac {-b+{\sqrt {\Delta }}}{2a}},}$

można postać iloczynową zapisać

${\displaystyle f(x)=a(x-x_{1})(x-x_{2}),}$

gdzie ${\displaystyle x_{1},x_{2}}$ są różnymi miejscami zerowymi funkcji kwadratowej^[3],

• ${\displaystyle \Delta =0,}$

wówczas ${\displaystyle x_{1}=x_{2}=p={\tfrac {-b}{2a}}}$^[3] i postać iloczynowa ma postać:

${\displaystyle f(x)=a(x-p)^{2}.}$

Funkcja kwadratowa ma jedno miejsce zerowe^[3] (któremu odpowiada dwukrotny pierwiastek wielomianu wyznaczającego funkcję; w związku z tym często mówi się wtedy nieprecyzyjnie, że miejsce zerowe jest podwójne)

• ${\displaystyle \Delta <0.}$

Funkcja kwadratowa nie ma postaci iloczynowej i nie ma miejsc zerowych w dziedzinie liczb rzeczywistych^[3].

W liczbach zespolonych istnieją zawsze dwa rozwiązania (por. zasadnicze twierdzenie algebry) dane jw. zgodnie z uwagą poczynioną w poprzedniej sekcji. Różnią się one wtedy znakiem (urojonego) wyrażenia ${\displaystyle {\sqrt {\Delta }},}$ są zatem sprzężone względem siebie.

Ze wzorów Viète’a wynika (także w dziedzinie zespolonej), że

${\displaystyle {\begin{cases}x_{1}+x_{2}=-{\tfrac {b}{a}},\\x_{1}x_{2}={\tfrac {c}{a}}.\end{cases}}}$

Wykres

Funkcja kwadratowa ${\displaystyle f(x)=ax^{2}+bx+c}$ dla różnych wartości współczynników ${\displaystyle a,b,c.}$

W kartezjańskim układzie współrzędnych na płaszczyźnie euklidesowej funkcja kwadratowa opisuje parabolę^[3]. Jej wierzchołkiem jest punkt ${\displaystyle (p,q),}$ gdzie ${\displaystyle p,q}$ są dane jw.^[3], który jest zarazem ekstremum funkcji kwadratowej. Ich zmiana powoduje więc przesunięcie wykresu o wektor ${\displaystyle [p,q]}$ względem początku układu współrzędnych.

Z definicji miejsca zerowego funkcji kwadratowej wynika, że są one punktami przecięcia wykresu paraboli z osią ${\displaystyle OX}$ układu. W szczególności ${\displaystyle p={\tfrac {x_{1}+x_{2}}{2}},}$ co oznacza, że odcięta wierzchołka paraboli jest średnią arytmetyczną miejsc zerowych (o ile istnieje choć jedno).

We układzie współrzędnych, przy zachowaniu skali:

• ${\displaystyle a>0}$ daje, iż ramiona paraboli są skierowane zgodnie ze zwrotem osi ${\displaystyle OY,}$ jeżeli ${\displaystyle a<0,}$ to są one skierowane przeciwnie^[3],
• zwiększanie ${\displaystyle |a|}$ sprawia, że wykres wydaje się bardziej „strzelisty”; jego zmniejszanie czyni wtedy wykres bardziej „rozłożystym”,
• zmiana ${\displaystyle b}$ powoduje zachowanie punktu przecięcia z osią ${\displaystyle OY}$ przy jednoczesnym przesuwaniu paraboli zgodnie ze zwrotem ${\displaystyle OX,}$ jeżeli ${\displaystyle b<0,}$ lub przeciwnie do niego, jeżeli ${\displaystyle b>0,}$
• parametr ${\displaystyle c}$ odpowiada za przesunięcie wykresu wzdłuż ${\displaystyle OY}$ zgodnie z jej zwrotem, gdy ${\displaystyle c>0,}$ lub przeciwnie do niego, gdy ${\displaystyle c<0.}$

Każda parabola będąca wykresem funkcji kwadratowej ma oś równoległą do osi ${\displaystyle OY.}$ Każde dwie parabole są podobne. Dokładniej, jeśli

${\displaystyle f_{1}(x)=a_{1}x^{2}+b_{1}x+c_{1},}$

${\displaystyle f_{2}(x)=a_{2}x^{2}+b_{2}x+c_{2},}$

to skala podobieństwa paraboli będącej wykresem ${\displaystyle f_{2}(x)}$ względem paraboli będącej wykresem ${\displaystyle f_{1}(x)}$ jest równa

${\displaystyle k=\left|{\frac {a_{1}}{a_{2}}}\right|.}$

Własności i przebieg zmienności

Niżej zakłada się, iż ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} ,\;f(x)=ax^{2}+bx+c{:}}$

• dziedzina i przeciwdziedzina: określona wszędzie; zbiorami wartości są przedział ${\displaystyle [q,\infty )}$ dla ${\displaystyle a>0}$ i przedział ${\displaystyle (-\infty ,q]}$ dla ${\displaystyle a<0,}$
• monotoniczność: maleje (rośnie) w przedziale ${\displaystyle (-\infty ,p],}$ po czym rośnie (maleje) w przedziale ${\displaystyle [p,\infty )}$ dla ${\displaystyle a>0\;(a<0),}$
• ciągłość, różniczkowalność, całkowalność: w całej dziedzinie, funkcja gładka; całkowalna w sensie Riemanna, Lebesgue’a itd.,
• pochodne:

${\displaystyle f'(x)=2ax+b,}$

${\displaystyle f''(x)=2a,}$

${\displaystyle f^{(n)}\equiv 0\;\;{}}$ dla ${\displaystyle n>2,}$

• funkcja pierwotna

${\displaystyle F(x)={\tfrac {1}{3}}ax^{3}+{\tfrac {1}{2}}bx^{2}+cx+C,}$

• ekstrema: jedno ekstremum globalne w punkcie ${\displaystyle p}$ (pierwsza pochodna zeruje się wyłącznie w tym punkcie): minimum dla ${\displaystyle a>0}$ i maksimum dla ${\displaystyle a<0}$ (zgodnie ze znakiem drugiej pochodnej),
• wypukłość: wypukła dla ${\displaystyle a>0}$ i wklęsła dla ${\displaystyle a<0}$ (zgodnie ze znakiem drugiej pochodnej),
• parzystość i nieparzystość: parzysta wyłącznie dla ${\displaystyle p=0,}$ nigdy nieparzysta,
• okresowość, punkty przegięcia i asymptoty: brak.

Konforemność

Funkcja kwadratowa ${\displaystyle w(z)=z^{2},}$ gdzie ${\displaystyle z\in \mathbb {C} \setminus \{0\}}$ jest odwzorowaniem równokątnym (konforemnym) przekształcającym płaszczyznę zespoloną (parametryzowaną zmienną) ${\displaystyle z}$ w dwulistną płaszczyznę (parametryzowaną zmienną) ${\displaystyle w.}$ Siatka izometryczna ${\displaystyle z}$ składa się z dwóch rodzin hiperbol:

${\displaystyle {\begin{cases}u=x^{2}-y^{2},\\v=2xy.\end{cases}}}$

Punktami stałymi tego odwzorowania są ${\displaystyle 0}$ oraz ${\displaystyle 1}$^[4].

Przykłady i zastosowania

• Pole koła jest kwadratową funkcją promienia (a zatem i średnicy).
• Pole rombu, na przykład kwadratu, jest kwadratową funkcją długości boku. To samo dotyczy innych wielokątów foremnych.
• Pole sfery jest kwadratową funkcją jej promienia (a zatem i średnicy).
• Pole wielościanów foremnych jest kwadratową funkcją długości krawędzi.
• Funkcja cosinus może być przybliżana funkcją kwadratową.
• Suma ciągu arytmetycznego, na przykład kolejnych liczb naturalnych (tak zwana liczba trójkątna), jest kwadratową funkcją liczby wyrazów.

• W kinematyce: dla ruchu jednostajnie zmiennego położenie (droga) jest kwadratową funkcją czasu. Przyspieszenie dośrodkowe jest kwadratową funkcją prędkości liniowej lub kątowej.
• W dynamice: dla wysokich prędkości opór ośrodka jest kwadratową funkcją prędkości.
• Energia kinetyczna jest kwadratową funkcją prędkości lub pędu.
• Energia potencjalna dla sprężyny lub innego obiektu spełniającego prawo Hooke’a jest kwadratową funkcją położenia.
• Rzut ukośny, przy zaniedbaniu oporów ruchu, jest opisany funkcją kwadratową. Jego trajektorią jest wykres funkcji kwadratowej, czyli parabola.

Zobacz też

• funkcja liniowa
• jednorodna funkcja kwadratowa
• równanie kwadratowe, równanie dwukwadratowe

Uwagi

Przypisy

Bibliografia

• Encyklopedia szkolna – matematyka. Warszawa: Wydawnictwa Szkolne i Pedagogiczne, 1990, s. 313. ISBN 83-02-02551-8.