Funkcja różnowartościowa

Diagram przemienny przedstawiający iniekcję jako funkcję odwracalną lewostronnie

Złożenie dwóch funkcji iniekcyjnych również jest iniekcją

Funkcja różnowartościowa, iniekcja^[1] (injekcja), funkcja 1-1 – funkcja, której każdy element przeciwdziedziny przyjmowany jest co najwyżej raz. Funkcja ${\displaystyle f\colon X\to Y}$ jest różnowartościowa wtedy i tylko wtedy, gdy dla dowolnych dwóch elementów ${\displaystyle a,b\in X}$ spełniony jest warunek^[2]:

${\displaystyle a\neq b\Rightarrow f(a)\neq f(b)}$;

stosuje się także równoważną postać powyższej implikacji (powstałą przez kontrapozycję):

${\displaystyle f(a)=f(b)\Rightarrow a=b}$.

Innymi słowy:

• przeciwobraz singletonu ma co najwyżej jeden element;
• istnieje lewostronna funkcja odwrotna: g∘f = id_X.

Termin iniekcja powstał najpóźniej w 1950 roku, kiedy to Saunders Mac Lane użył go w jednym z amerykańskich czasopism matematycznych^[3].

• 

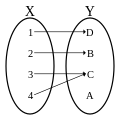
  Iniekcyjna funkcja niesurjekcyjna (iniekcja, nie bijekcja)

• 

  Iniekcyjna surjekcyjna funkcja (bijekcja)

• 

  Nieinjekcyjna surjekcyjna funkcja (surjekcja, nie bijekcja)

• 

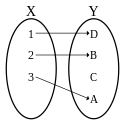
  Nieinjekcyjna niesurjekcyjna funkcja (również nie bijekcja)

Przykłady i własności

• numer PESEL – dwie osoby nie mogą mieć jednakowego;
• transliteracje to iniekcje między zbiorami ciągów (krotek) znaków. Niektóre transliteracje są też iniekcjami między zbiorami samych znaków;
• pierwiastek dowolnego stopnia naturalnego;
• funkcja wykładnicza zmiennej rzeczywistej; przyjmuje wyłącznie wartości nieujemne, przez co nie jest „na” przy takiej samej przeciwdziedzinie;
• funkcje kołowe;
• dowolna inna funkcja ściśle monotoniczna (ściśle rosnąca lub ściśle malejąca);
• macierze, w których każdy element jest inny; np. w standardowym sudoku (9×9) każdy z dziewięciu głównych kwadratów 3×3 jest iniekcją do zbioru cyfr dziesiętnych;
• negacja na zbiorze zdań oznajmujących danego języka;
• wszelkie bijekcje.

Wprost z definicji wynika, że iniekcja nie może być funkcją parzystą ani okresową, ponieważ własności te są zdefiniowane przez równość wartości dla różnych argumentów. Iniekcjami nie są również:

• wielomiany rzeczywiste stopnia parzystego, nawet jeśli nie są funkcjami parzystymi; np. (x−1)⁴;
• funkcja Collatza – jest sumą mnogościową iniekcji na zbiorach liczb parzystych i nieparzystych, jednak dla argumentu parzystego i nieparzystego może przyjąć jednakową wartość. Przykładowo c(3) = c(20) = 10.

Zobacz też

• funkcja „na” (suriekcja)
• monomorfizm
• Twierdzenie Cantora-Bernsteina-Schrödera – o konsekwencji istnienia pewnych iniekcji;
• Zasada szufladkowa Dirichleta – fakt nieistnienia pewnych iniekcji.

Przypisy