Funkcje hiperboliczne odwrotne

Pole zakreskowanego obszaru odpowiada połowie wyniku funkcji area

Pole zakreskowanego obszaru odpowiada połowie wyniku funkcji odwrotnych do trygonometrycznych

Funkcje hiperboliczne odwrotne, funkcje polowe, funkcje area, areafunkcje – funkcje odwrotne do funkcji hiperbolicznych^[1]. Ich nazwy odzwierciedlają fakt, że wartości tych funkcji są równe polom odpowiednich wycinków hiperboli jednostkowej ${\displaystyle x^{2}-y^{2}=1,}$ w analogiczny sposób, jak funkcje odwrotne do trygonometrycznych są równe polom wycinków koła jednostkowego ${\displaystyle x^{2}+y^{2}=1.}$

Definiuje się je następującymi wzorami:

${\displaystyle \operatorname {arsinh} \ x=\ln(x+{\sqrt {x^{2}+1}})}$

(area sinus hiperboliczny) – funkcja odwrotna do sinusa hiperbolicznego^[2],

${\displaystyle \operatorname {arcosh} \ x=\ln(x+{\sqrt {x^{2}-1}})=\ln(x+{\sqrt {x-1}}{\sqrt {x+1}})}$

(area cosinus hiperboliczny) – funkcja odwrotna do cosinusa hiperbolicznego^[3],

${\displaystyle \operatorname {artgh} \ x=\ln {\sqrt {\frac {1+x}{1-x}}}={\frac {1}{2}}\ln {\frac {1+x}{1-x}}}$

(area tangens hiperboliczny) – funkcja odwrotna do tangensa hiperbolicznego^[4],

${\displaystyle \operatorname {arctgh} \ x=\ln {\sqrt {\frac {x+1}{x-1}}}={\frac {1}{2}}\ln {\frac {x+1}{x-1}}}$

(area cotangens hiperboliczny) – funkcja odwrotna do cotangensa hiperbolicznego^[5],

${\displaystyle \operatorname {arsech} \ x=\ln \left({\sqrt {{\frac {1}{x^{2}}}-1}}+{\frac {1}{x}}\right)=\ln \left({\sqrt {{\frac {1}{x}}-1}}{\sqrt {{\frac {1}{x}}+1}}+{\frac {1}{x}}\right)}$

(area secans hiperboliczny) – funkcja odwrotna do secansa hiperbolicznego,

${\displaystyle \operatorname {arcsch} \ x=\ln \left({\sqrt {1+{\frac {1}{x^{2}}}}}+{\frac {1}{x}}\right)}$

(area cosecans hiperboliczny) – funkcja odwrotna do cosecansa hiperbolicznego.

Area sinus

(c) I, Harkonnen2, CC-BY-SA-3.0

Area sinus hiperboliczny

Area cosinus hiperboliczny, górna gałąź krzywej

Area tangens hiperboliczny

Area cotangens hiperboliczny

Area secans hiperboliczny

Area cosecans hiperboliczny

Dziedziną i przeciwdziedziną funkcji jest zbiór liczb rzeczywistych ${\displaystyle \mathbb {R} .}$ Funkcja w punkcie ${\displaystyle x=0}$ ma punkt przegięcia, jest rosnąca na całej dziedzinie i nie ma asymptot.

Area cosinus

Area cosinus hiperboliczny, jako funkcja odwrotna do funkcji parzystej, jest niejednoznaczny. Funkcja ma dwie gałęzie, które obie są określone tylko na przedziale ${\displaystyle [1+\infty ).}$ Ogólnie dla liczb rzeczywistych:

${\displaystyle \operatorname {arcosh} \ x=\ln(x\pm {\sqrt {x^{2}-1}})}$

Poszczególne gałęzie są dane wzorami:

${\displaystyle \operatorname {arcosh} _{1}\ x=\ln(x+{\sqrt {x^{2}-1}})}$

oraz

${\displaystyle \operatorname {arcosh} _{2}\ x=\ln(x-{\sqrt {x^{2}-1}})}$

Dziedziną funkcji jest przedział ${\displaystyle [1,\infty ).}$

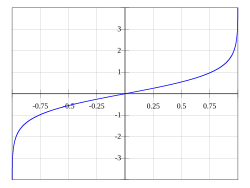
Area tangens

Dziedziną funkcji jest przedział ${\displaystyle (-1,1),}$ jest nieparzysta oraz rosnąca. Ma dwie asymptoty: ${\displaystyle x=-1,\;x=1.}$

Area cotangens

Dziedziną funkcji area cotangens jest przedział ${\displaystyle (-\infty ,-1)\cup (1,\infty ).}$ Funkcja nie ma ekstremów i punktów przegięcia, ma 3 asymptoty: ${\displaystyle y=0,\;x=-1,\;x=1.}$

Area secans

Dziedziną funkcji jest przedział ${\displaystyle (0,1].}$ Funkcja ma asymptotę o równaniu ${\displaystyle x=0.}$

Area cosecans

Dziedziną jest ${\displaystyle \mathbb {R} \setminus \{0\}.}$ Funkcja ma dwie asymptoty: ${\displaystyle x=0}$ i ${\displaystyle y=0.}$

Funkcje hiperboliczne odwrotne jako całki

${\displaystyle \int {\frac {dx}{\sqrt {1-x^{2}}}}=\arcsin \ x+C=-\arccos \ x+{\frac {\pi }{2}}+C}$

${\displaystyle \int {\frac {dx}{\sqrt {x^{2}+1}}}=\operatorname {arsinh} \ x+C=\ln(x+{\sqrt {x^{2}+1}})+C}$

${\displaystyle \int {\frac {dx}{\sqrt {x^{2}-1}}}=\operatorname {arcosh} \ x+C=\ln(x+{\sqrt {x^{2}-1}})+C}$

${\displaystyle \int {\sqrt {1-x^{2}}}\ dx={\frac {1}{2}}\left(\arcsin \ x+x{\sqrt {1-x^{2}}}\right)+C}$

${\displaystyle \int {\sqrt {x^{2}+1}}\ dx={\frac {1}{2}}\left(\operatorname {arsinh} \ x+x{\sqrt {x^{2}+1}}\right)+C\ {}}$${\displaystyle ={\frac {1}{2}}\left(\ln(x+{\sqrt {x^{2}+1}})+x{\sqrt {x^{2}+1}}\right)+C}$

${\displaystyle \int {\sqrt {x^{2}-1}}\ dx={\frac {1}{2}}\left(-\operatorname {arcosh} \ x+x{\sqrt {x^{2}-1}}\right)+C\ {}}$${\displaystyle ={\frac {1}{2}}\left(-\ln(x+{\sqrt {x^{2}-1}})+x{\sqrt {x^{2}-1}}\right)+C}$

${\displaystyle \int {\frac {dx}{1+x^{2}}}=\operatorname {arctg} \ x+C}$

${\displaystyle \int {\frac {dx}{1-x^{2}}}={\frac {1}{2}}\ln \left|{\frac {1+x}{1-x}}\right|+C={\begin{cases}\operatorname {artgh} \ x+C&\quad {\text{dla}}&\ |x|<1\\\operatorname {arctgh} \ x+C&\quad {\text{dla}}&\ |x|>1\end{cases}}}$

Związek z funkcjami cyklometrycznymi

${\displaystyle \operatorname {arsinh} x=i\arcsin(-ix)}$

${\displaystyle \operatorname {arcosh} x=i\arccos x}$

${\displaystyle \operatorname {artgh} x=i\operatorname {arctg} (-ix)}$

Pochodne funkcji area

• ${\displaystyle {\frac {d}{dx}}\operatorname {arsinh} \ x={\frac {1}{\sqrt {x^{2}+1}}}}$
• pochodnymi gałęzi area cosinusa hiperbolicznego są:

${\displaystyle {\frac {d}{dx}}\operatorname {arcosh} _{1}\ x={\frac {1}{\sqrt {x^{2}-1}}}}$

${\displaystyle {\frac {d}{dx}}\operatorname {arcosh} _{2}\ x={\frac {-1}{\sqrt {x^{2}-1}}}}$

• ${\displaystyle {\frac {d}{dx}}\operatorname {artgh} \ x={\frac {1}{1-x^{2}}}}$
• ${\displaystyle {\frac {d}{dx}}\operatorname {arctgh} \ x={\frac {1}{1-x^{2}}}}$
• ${\displaystyle {\frac {d}{dx}}\operatorname {arsech} \ x=-{\frac {1}{x(x+1){\sqrt {\frac {1-x}{1+x}}}}}}$
• ${\displaystyle {\frac {d}{dx}}\operatorname {arcsch} \ x=-{\frac {1}{x^{2}{\sqrt {1+{\frac {1}{x^{2}}}}}}}}$

Właściwości analityczne

• Area sinus hiperboliczny jest funkcją nieparzystą i rosnącą.
• Funkcją odwrotną dla pierwszej gałęzi area cosinusa hiperbolicznego jest cosinus hiperboliczny dla argumentów większych od zera; dla drugiej gałęzi cosinus hiperboliczny dla argumentów mniejszych od zera.

Przypisy