Granica funkcji

Granica funkcji – wartość, do której obrazy danej funkcji zbliżają się nieograniczenie dla argumentów dostatecznie bliskich wybranemu punktowi. Funkcjonują dwie równoważne definicje podane przez Augustina Louisa Cauchy’ego oraz Heinricha Eduarda Heinego.

Historia

Pojęcie to znane było intuicyjnie już w starożytności. Stosowano je wówczas do obliczania pól figur geometrycznych za pomocą tzw. metody wyczerpywania, która polegała na wpisywaniu w daną figurę geometryczną ciągu figur o znanych polach (pomysł wykorzystywany jest do dzisiaj w nieco zmodyfikowanej formie jako całka oznaczona, np. Lebesgue’a). Łaciński termin oznaczający granicę, „limes”, pojawił się w XVII wieku w pracach Newtona oraz Leibniza w związku z próbami uściślenia tego pojęcia.

Współczesna definicja granicy funkcji powstała w XIX wieku wraz z rozwojem analizy matematycznej. Pierwszą ścisłą definicję granicy funkcji, sformułowaną za pomocą pojęć arytmetycznych, podał Cauchy, a współczesne brzmienie nadał jej Weierstrass^[1].

Granica w punkcie

Funkcja ${\displaystyle f\colon A\to \mathbb {R} }$ określona na zbiorze ${\displaystyle A\subseteq \mathbb {R} }$ ma w punkcie skupienia ${\displaystyle x_{0}}$ tego zbioru granicę równą ${\displaystyle g,}$ jeżeli spełniony jest jeden z równoważnych warunków

1. definicja Heinego:

dla każdego ciągu ${\displaystyle (x_{n})}$ takiego, że dla dowolnego ${\displaystyle n\in \mathbb {N} ,x_{n}\in A,\ x_{n}\neq x_{0}}$ oraz ${\displaystyle x_{n}}$dąży do ${\displaystyle x_{0}}$, ciąg wartości funkcji ${\displaystyle (f(x_{n}))}$ dąży do ${\displaystyle g}$ gdy ${\displaystyle n\to \infty }$^[1];

2. definicja Cauchy’ego:

${\displaystyle \forall _{\varepsilon >0}\;\exists _{\delta >0}\;\forall _{x\in A}\;(0<|x-x_{0}|<\delta \implies |f(x)-g|<\varepsilon ),}$

co czytamy następująco: dla każdej liczby ${\displaystyle \varepsilon >0}$ istnieje liczba ${\displaystyle \delta >0}$ taka, że dla każdego ${\displaystyle x\in A}$ z nierówności ${\displaystyle 0<|x-x_{0}|<\delta }$ wynika nierówność ${\displaystyle |f(x)-g|<\varepsilon .}$

3. definicja przez ciągłość^[2]: ${\displaystyle g}$ jest taką wartością, którą należy nadać funkcji ${\displaystyle f}$ w punkcie ${\displaystyle x_{0}}$ by była w tym punkcie ciągła:

${\displaystyle h(x)=\left\{{f(x){\text{ dla }}x\neq x_{0} \atop g{\text{ dla }}x=x_{0}}\right.}$ jest ciągła w ${\displaystyle x_{0}.}$ (Ta definicja stosuje się do wszystkich funkcji, nie tylko liczbowo-liczbowych.) Aby móc stosować tę definicję gdy ${\displaystyle x_{0}}$ lub ${\displaystyle g}$ są równe ${\displaystyle +\infty }$ lub ${\displaystyle -\infty }$ wystarczy rozważać rozszerzony zbiór liczb rzeczywistych z odpowiednimi otoczeniami ${\displaystyle +\infty }$ i ${\displaystyle -\infty }$.

Warunek ${\displaystyle 0<|x-x_{0}|}$ w definicji Cauchy’ego oznacza, że nie wymagamy ${\displaystyle |f(x_{0})-g|<\varepsilon .}$ W definicji przez ciągłość nie musimy wykluczać tego wymagania dla funkcji ${\displaystyle h}$, bo sprowadza się ono do warunku ${\displaystyle |g-g|<\varepsilon ,}$ który jest oczywiście spełniony, bo ${\displaystyle \varepsilon >0.}$

Jeżeli istnieje granica funkcji ${\displaystyle f}$ w punkcie ${\displaystyle x_{0}}$ i jest równa ${\displaystyle g,}$ to piszemy

${\displaystyle f(x)\to g}$ ${\displaystyle (x\to x_{0})}$

i czytamy „${\displaystyle f(x)}$ dąży do ${\displaystyle g,}$ gdy ${\displaystyle x}$ dąży do ${\displaystyle x_{0}}$”^[2]

lub równoważnie

${\displaystyle \lim _{x\to x_{0}}f(x)=g,}$

co czytamy: „limes ${\displaystyle f(x)}$ przy ${\displaystyle x}$ dążącym do ${\displaystyle x_{0}}$ równa się ${\displaystyle g}$”.

${\displaystyle x\to x_{0}^{+}\neq x\to x_{0}^{-}.}$ Dlatego granica jako ${\displaystyle x\to x_{0}}$ nie istnieje.

Przykłady

Nie istnieje granica

${\displaystyle \lim _{x\to 0}~{\frac {1}{x}}}$

(żadna liczba, nawet 0, nie spełnia defnicji granicy). Natomiast istnieją obie granice jednostronne:

${\displaystyle \lim _{x\to 0^{+}}~{\frac {1}{x}}=+\infty }$

${\displaystyle \lim _{x\to 0^{-}}~{\frac {1}{x}}=-\infty }$

Nie istnieje granica

${\displaystyle \lim _{x\to 0}~\sin {\frac {1}{x}}}$

(żadna liczba, nawet 0, nie spełnia definicji granicy). Nie istnieją też granice jednostronne.

Istnieje granica ${\displaystyle \lim _{x\to \infty }~{\frac {1}{x}}}$ i jest równa 0.

Istnieje granica ${\displaystyle \lim _{x\to 0}~x\cdot \sin {\frac {1}{x}}}$ i jest równa 0.

Granica jednostronna

Granica jednostronna jest wspólną nazwą dla granicy lewostronnej i prawostronnej. Wyżej rozważaną granicę nazywa się czasami (w opozycji do ukazanej w tej sekcji) obustronną. Jeżeli granice lewo- i prawostronna istnieją i są sobie równe, to są one granicą obustronną; twierdzenie odwrotne też jest prawdziwe: jeżeli istnieje granica obustronna to obie granice jednostronne istnieją i są jej równe (o ile punkt, w którym obliczamy granice jest odpowiednio lewostronnym lub prawostronnym punktem skupienia dziedziny funkcji).

Liczba ${\displaystyle g}$ jest granicą lewostronną (odpowiednio: prawostronną) funkcji ${\displaystyle f}$ w lewostronnym (odpowiednio: prawostronnym) punkcie skupienia ${\displaystyle x_{0}}$ dziedziny, co zapisuje się

${\displaystyle f(x)\to g}$ przy ${\displaystyle x\to x_{0}^{-}}$ (odpowiednio: ${\displaystyle f(x)\to g}$ przy ${\displaystyle x\to x_{0}^{+}}$)

lub

${\displaystyle \lim _{x\to x_{0}^{-}}~f(x)=g}$ (odpowiednio: ${\displaystyle \lim _{x\to x_{0}^{+}}~f(x)=g}$),

gdy spełnione są warunki określone w jakiejkolwiek z następujących dwu równoważnych definicji:

definicja Heinego

dla każdego ciągu ${\displaystyle (x_{n})}$ takiego, że dla dowolnego ${\displaystyle n\in \mathbb {N} \ x_{n}\in A,\ x_{n}<x_{0}}$ (odpowiednio: ${\displaystyle x_{n}>x_{0}}$)   oraz ${\displaystyle \lim _{n\to \infty }~x_{n}=x_{0},}$
ciąg wartości funkcji ${\displaystyle (f(x_{n}))}$ dąży do ${\displaystyle g}$ przy ${\displaystyle n\to \infty ;}$

definicja Cauchy’ego

${\displaystyle \forall _{\varepsilon >0}\;\exists _{\delta >0}\;\forall _{x\in A}\;(x_{0}-\delta <x<x_{0}\implies |f(x)-g|<\varepsilon )}$ (odpowiednio: ${\displaystyle \forall _{\varepsilon >0}\;\exists _{\delta >0}\;\forall _{x\in A}\;(x_{0}<x<x_{0}+\delta \implies |f(x)-g|<\varepsilon )}$).

Granica niewłaściwa

Funkcja ${\displaystyle f}$ ma w punkcie ${\displaystyle x_{0}}$ granicę niewłaściwą ${\displaystyle +\infty ,}$ co zapisuje się

${\displaystyle f(x)\to +\infty }$ przy ${\displaystyle x\to x_{0}}$

lub

${\displaystyle \lim _{x\to x_{0}}~f(x)=+\infty ,}$

gdy spełnione są warunki, określone w jakiejkolwiek z następujących dwu równoważnych definicji:

definicja Heinego

dla każdego ciągu ${\displaystyle (x_{n})}$ takiego, że ${\displaystyle x_{n}\in A,x_{n}\neq x_{0}}$ oraz ${\displaystyle \lim _{n\to \infty }~x_{n}=x_{0}}$ ciąg wartości funkcji ${\displaystyle (f(x_{n}))}$ dąży do ${\displaystyle +\infty }$ przy ${\displaystyle n\to +\infty ;}$

definicja Cauchy’ego

${\displaystyle \forall _{M>0}\;\exists _{\delta >0}\;\forall _{x\in A}\;(0<|x-x_{0}|<\delta \implies f(x)>M).}$

Analogicznie definiuje się i oznacza się granicę niewłaściwą ${\displaystyle -\infty {:}}$ trzeba tylko wszędzie zamienić ${\displaystyle +\infty }$ na ${\displaystyle -\infty ,}$ a definicję Cauchy’ego zapisać tak:

${\displaystyle \forall _{M>0}\;\exists _{\delta >0}\;\forall _{x\in A}\;(0<|x-x_{0}|<\delta \implies f(x)<-M).}$

Analogicznie określa się niewłaściwe granice lewo- i prawostronną: trzeba w sposób naturalny skombinować informację z tej i poprzedniej podsekcji.

Granica w nieskończoności

Granica tej funkcji w nieskończoności istnieje

Funkcja ${\displaystyle f}$ określona dla wszystkich ${\displaystyle x>a}$ (odpowiednio: ${\displaystyle x<a}$) ma granicę ${\displaystyle g}$ w plus (odpowiednio: minus) nieskończoności, co zapisuje się

${\displaystyle f(x)\to g}$ przy ${\displaystyle x\to +\infty }$ (odpowiednio: ${\displaystyle x\to -\infty }$)

lub

${\displaystyle \lim _{x\to +\infty }~f(x)=g}$ (odpowiednio: ${\displaystyle \lim _{x\to -\infty }~f(x)=g}$),

gdy spełnione są warunki, określone w jakiejkolwiek z następujących dwóch równoważnych definicji:

definicja Heinego

dla każdego ciągu ${\displaystyle (x_{n})}$ takiego, że dla każdego ${\displaystyle n\in \mathbb {N} \ x_{n}>a}$ oraz ${\displaystyle x_{n}\to +\infty }$ (odpowiednio: dla każdego ${\displaystyle n\in \mathbb {N} \ x_{n}<a}$ oraz ${\displaystyle x_{n}\to -\infty }$),
ciąg wartości funkcji ${\displaystyle f(x_{n})}$ dąży do ${\displaystyle g}$ przy ${\displaystyle n\to \infty ;}$

definicja Cauchy’ego

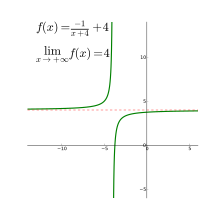
Asymptota pozioma ${\displaystyle y=4}$

${\displaystyle \forall _{\varepsilon >0}\;\exists _{\alpha \in \mathbb {R} }\;\forall _{x>\alpha }\;|f(x)-g|<\varepsilon }$ (odpowiednio ${\displaystyle \forall _{\varepsilon >0}\;\exists _{\alpha \in \mathbb {R} }\;\forall _{x<\alpha }\;|f(x)-g|<\varepsilon }$).

Granica niewłaściwa w nieskończoności

Funkcja ${\displaystyle f}$ określona na przedziale ${\displaystyle (a,+\infty )}$ ma w nieskończoności granicę niewłaściwą ${\displaystyle +\infty ,}$ co zapisuje się

${\displaystyle f(x)\to +\infty }$ przy ${\displaystyle x\to +\infty }$

lub

${\displaystyle \lim _{x\to +\infty }~f(x)=+\infty ,}$

gdy spełnione są warunki określone w jakiejkolwiek z następujących dwóch równoważnych definicji:

definicja Heinego

dla każdego ciągu ${\displaystyle (x_{n})}$ takiego, że dla każdego ${\displaystyle n\in \mathbb {N} \ x_{n}>a}$ oraz ${\displaystyle x_{n}\to +\infty ,}$ ciąg wartości funkcji ${\displaystyle f(x_{n})}$ dąży do ${\displaystyle +\infty }$ przy ${\displaystyle n\to \infty ;}$

definicja Cauchy’ego

${\displaystyle \forall _{M>0}\;\exists _{\alpha \in \mathbb {R} }\;\forall _{x>\alpha }\;f(x)>M.}$

Analogicznie definiuje się:

• granicę niewłaściwą ${\displaystyle -\infty }$ funkcji w ${\displaystyle +\infty ,}$
• granicę niewłaściwą ${\displaystyle +\infty }$ funkcji w ${\displaystyle -\infty ,}$
• granicę niewłaściwą ${\displaystyle -\infty }$ funkcji w ${\displaystyle -\infty .}$

Własności

• Jeśli funkcje ${\displaystyle f}$ i ${\displaystyle g,}$ określone na zbiorze ${\displaystyle A\subseteq \mathbb {R} ,}$ mają granice właściwe ${\displaystyle \lim _{x\to x_{0}}~f(x)=a}$ i ${\displaystyle \lim _{x\to x_{0}}~g(x)=b,}$ to:
  • ${\displaystyle \lim _{x\to x_{0}}~(f(x)\pm g(x))=a\pm b,}$
  • ${\displaystyle \lim _{x\to x_{0}}~(f(x)\cdot g(x))=a\cdot b,}$
  • ${\displaystyle \lim _{x\to x_{0}}~{\tfrac {f(x)}{g(x)}}={\tfrac {a}{b}},}$ gdy ${\displaystyle g(x)\neq 0}$ oraz ${\displaystyle b\neq 0.}$

Uwaga: twierdzenie to jest prawdziwe również dla granic w nieskończoności.

• • Należy pamiętać, że twierdzenie odwrotne nie jest prawdziwe, np. to, że ${\displaystyle \lim _{x\to \infty }~{\tfrac {\sin x}{x}}=0,}$ nie oznacza, że istnieją granice ${\displaystyle \lim _{x\to \infty }~\sin x}$ czy ${\displaystyle \lim _{x\to \infty }~{\tfrac {1}{x}}.}$ W podanym przykładzie granica ${\displaystyle \lim _{x\to \infty }~\sin x}$ nie istnieje, natomiast ${\displaystyle \lim _{x\to \infty }~{\tfrac {1}{x}}=0.}$
• Twierdzenie o granicy funkcji złożonej.

Jeśli funkcja ${\displaystyle f\colon A\to \mathbb {R} }$ ma w punkcie ${\displaystyle x_{0}}$ granicę ${\displaystyle \lim _{x\to x_{0}}~f(x)=y_{0},}$ funkcja ${\displaystyle g\colon B\to \mathbb {R} }$ ma w punkcie ${\displaystyle y_{0}}$ granicę ${\displaystyle \lim _{y\to y_{0}}~g(y)=z_{0},}$ przy czym ${\displaystyle x_{0}}$ i ${\displaystyle y_{0}}$ są odpowiednio punktami skupienia zbiorów ${\displaystyle A\cap f^{-1}(B)}$ oraz ${\displaystyle B,}$ przy czym ${\displaystyle f(x)\neq y_{0}}$ dla każdego ${\displaystyle x}$ z pewnego sąsiedztwa punktu ${\displaystyle x_{0},}$ to ${\displaystyle \lim _{x\to x_{0}}~(g\circ f)(x)=\lim _{y\to y_{0}}~g(y)=z_{0}.}$

Wymienione niżej własności są prawdziwe także w przypadku granic jednostronnych i w nieskończoności:

• ${\displaystyle \lim _{x\to x_{0}}~f(x)=\pm \infty \implies \lim _{x\to x_{0}}~{\tfrac {1}{f(x)}}=0,}$
• ${\displaystyle \lim _{x\to x_{0}}~f(x)=0}$ oraz ${\displaystyle f(x)>0\;{\big (}f(x)<0{\big )}}$ w pewnym sąsiedztwie ${\displaystyle x_{0}\implies \lim _{x\to x_{0}}~{\tfrac {1}{f(x)}}=\pm \infty ,}$
• ${\displaystyle \lim _{x\to x_{0}}~f(x)=\pm \infty }$ oraz ${\displaystyle c>0\implies \lim _{x\to x_{0}}~cf(x)=\pm \infty ,}$
• ${\displaystyle \lim _{x\to x_{0}}~f(x)=\pm \infty }$ oraz ${\displaystyle c<0\implies \lim _{x\to x_{0}}cf(x)=\mp \infty ,}$
• ${\displaystyle \lim _{x\to x_{0}}f(x)=\pm \infty }$ oraz ${\displaystyle 0<a\leqslant h(x)}$ w pewnym sąsiedztwie ${\displaystyle x_{0}\implies \lim _{x\to x_{0}}~f(x)\cdot h(x)=\pm \infty ,}$
• ${\displaystyle \lim _{x\to x_{0}}f(x)=\pm \infty }$ oraz ${\displaystyle h(x)\leqslant a<0}$ w pewnym sąsiedztwie ${\displaystyle x_{0}\implies \lim _{x\to x_{0}}~f(x)\cdot h(x)=\mp \infty .}$

Zobacz też

• granica ciągu
• granice dolna i górna
• reguła de l’Hospitala
• twierdzenie o trzech ciągach (funkcjach)

Przypisy

Bibliografia

• Encyklopedia szkolna – matematyka. Warszawa: WSiP, 1996. ISBN 83-02-02551-8.