Grupa Coxetera

Grupą Coxetera – grupa z wyróżnionym układem generatorów ${\displaystyle \{r_{i}:i\in I\},}$ którego elementy spełniają następujący układ relacji:

${\displaystyle (r_{i}r_{j})^{n_{ij}}=1{\text{ dla }}i,j\in I,}$

gdzie:

${\displaystyle n_{ii}=1,}$ czyli ${\displaystyle r_{i}^{2}=1}$ dla dowolnego ${\displaystyle i\in I,}$

${\displaystyle n_{ij}=n_{ji}\in \mathbb {Z} \cup \{\infty \}}$ dla ${\displaystyle i,j\in I,i\neq j,}$ przy czym ${\displaystyle n_{ij}\geqslant 2;}$ dla ${\displaystyle n_{ij}=\infty }$ nie istnieje relacja między ${\displaystyle r_{i}\,{}}$ a ${\displaystyle {}\,r_{j}}$^[1].

Nazwa pojęcia pochodzi od nazwiska Harolda Coxetera^[2]. Grupy tego rodzaju są rozważane w teorii grup dyskretnych jako uogólnienie grup odbić^[3] generowanych przez odbicia względem hiperpowierzchni w przestrzeni euklidesowej. Każda grupa odbić jest grupą Coxetera, jeśli jej generatorami są odbicia względem hiperpowierzchni ograniczających wielościan fundamentalny.

Macierz ${\displaystyle (n_{ij}),}$ gdzie ${\displaystyle i,j\in I}$ nazywa się macierzą Coxetera danej grupy Coxetera. Macierz ta i sama grupa może być zadana za pomocą grafu Coxetera – grafu o wierzchołkach ${\displaystyle \{a_{i}:i\in I\},}$ w którym wierzchołki ${\displaystyle a_{i}}$ i ${\displaystyle a_{j}}$ są połączone ${\displaystyle (n_{ij}-2)}$-krotną krawędzią, jeśli ${\displaystyle n_{ij}<\infty }$ (w szczególności nie są w ogóle połączone, jeśli ${\displaystyle n_{ij}=2}$) i są połączone grubą krawędzią, jeśli ${\displaystyle n_{ij}=\infty .}$ Czasem zamiast łączyć wierzchołki grafu krawędziami wielokrotnymi, łączy się je jedną krawędzią ze znakiem ${\displaystyle n_{ij}}$ nad nią.

Własności

• Jeśli ${\displaystyle n_{ij}=2,}$ to mnożenie ${\displaystyle r_{i}}$ przez ${\displaystyle r_{j}}$ jest przemienne.
• ${\displaystyle n_{ij}}$ jest rzędem elementu ${\displaystyle r_{i}r_{j}.}$

Przykłady

• Każda grupa generowana przez dwa elementy rzędu 2 jest grupą Coxetera o macierzy postaci ${\displaystyle \left[{\begin{smallmatrix}2&m\\m&2\end{smallmatrix}}\right].}$ Jej graf Coxetera:

• Grupa symetryczna ${\displaystyle {\mathfrak {S}}_{n}}$ jest grupą Coxetera względem generatorów ${\displaystyle r_{i}=(i,i+1)}$ dla ${\displaystyle i=1,2,\dots ,n-1}$ (${\displaystyle r_{i}}$ jest transpozycją elementów ${\displaystyle i}$ i ${\displaystyle i+1}$). Jej graf Coxetera:

• Macierzą Coxetera grupy ${\displaystyle {\mathfrak {S}}_{4}}$ jest:

${\displaystyle {\begin{bmatrix}2&3&2\\3&2&3\\2&3&2\end{bmatrix}}}$

• Grupa ${\displaystyle PGL=GL_{2}(\mathbb {Z} )/\{\pm 1\}}$ jest grupą Coxetera względem generatorów:

${\displaystyle r_{1}=\left\{\pm {\begin{bmatrix}-1&0\\0&1\end{bmatrix}}\right\},\;r_{2}=\left\{\pm {\begin{bmatrix}-1&0\\1&1\end{bmatrix}}\right\},\;r_{3}=\left\{\pm {\begin{bmatrix}0&-1\\1&0\end{bmatrix}}\right\}.}$

Jej graf Coxetera:

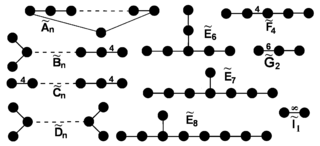
Skończone grupy Coxetera

H.S.M. Coxeter w roku 1934 znalazł wszystkie grupy odbić w n-wymiarowej przestrzeni euklidesowej ${\displaystyle E^{n}}$ i wykazał, że są one grupami Coxetera^[4]. W następnej pracy^[5] wykazał, że każda skończona grupa Coxetera jest izomorficzna z pewną grupą odbić w ${\displaystyle E^{n},}$ której elementy mają wspólny punkt stały. W ten sposób otrzymał klasyfikację grup skończonych Coxetera.

Grafy (diagramy) Coxetera skończonych grup Coxetera^[6].

Nieskończone grupy Coxetera

Wśród nieskończonych grup Coxetera można wyróżnić grupy paraboliczne, izomorficzne z pewną grupą odbić w przestrzeni euklidesowej ${\displaystyle E^{n}}$ i grupy hiperboliczne, izomorficzne z pewną grupą odbić przestrzeni hiperbolicznej ${\displaystyle L^{n},}$ elementy których nie mają wspólnej hiperpłaszczyzny niezmienniczej o wymiarze mniejszym od n (w przypadku hiperbolicznym za hiperpłaszczyznę należy uważać również punkt w nieskończoności^[7]).

Wszystkie paraboliczne grupy Coxetera zostały znalezione przez H.S.M. Coxetera, który udowodnił, że są to afiniczne grupy Weyla z teorii półprostych grup Liego.

Diagramy Coxetera afinicznych grup Weyla

Związek z wielościanami

Jeśli przestrzeń jest n-wymiarową sferą, przestrzenią euklidesową lub przestrzenią hiperboliczną, to grupa odbić jest generowana przez odbicia ${\displaystyle r_{i}}$ względem hiperpowierzchni ${\displaystyle H_{i},}$ ograniczających wielościan fundamentalny ${\displaystyle P}$ tej grupy. Względem tego układu generatorów grupa odbić jest grupą Coxetera o relacjach zdefiniowanych następująco:

1. jeśli ściany ${\displaystyle H_{i}\cap P}$ i ${\displaystyle H_{j}\cap P}$ przylegają do siebie i kąt między nimi jest równy ${\displaystyle \alpha _{ij},}$ to ${\displaystyle {r_{i}r_{j}}^{n_{ij}}=1,}$ gdzie ${\displaystyle n_{ij}={\frac {\pi }{\alpha _{ij}}},}$
2. jeśli ściany ${\displaystyle H_{i}\cap P}$ i ${\displaystyle H_{j}\cap P}$ nie przylegają do siebie, to ${\displaystyle n_{ij}=\infty .}$

Wielościany fundamentalne grup Coxetera nazywają się wielościanami Coxetera. Wielościanami Coxetera można wypełnić przestrzeń. Mają więc związek z parkietażami i krystalografią.

Przykłady

• Wielościany Coxetera w n-wymiarowej przestrzeni euklidesowej:
  • 2n-komórka foremna ${\displaystyle \{(x_{1},\dots ,x_{n}):0\leqslant x_{i}\leqslant 1,i=1,\dots ,n\},}$
  • (n + 1)-komórka (n-sympleks) ${\displaystyle \{(x_{1},\dots ,x_{n}):0\leqslant x_{1}\cdots \leqslant x_{n}\leqslant 1\}.}$
• Wielościany Coxetera w n-wymiarowej sferze:
  • n-wymiarowy sympleks foremny o boku ${\displaystyle \pi /2.}$
• Wielościany Coxetera w n-wymiarowej przestrzeni hiperbolicznej:
  • k-wielokąt foremny o kącie ${\displaystyle \pi /m}$ w przestrzeni 2-wymiarowej,
  • dwunastościan foremny (dodekaedr) prostokątny w przestrzeni 3-wymiarowej,
  • 120-ścian foremny prostokątny w przestrzeni 4-wymiarowej.

Przypisy

Bibliografia

• Математическая энциклопедия. И.М. Виноградов (red.). T. 2. Москва: Советская энциклопедия, 1979.
• Harold Scott MacDonald Coxeter. Discrete groups generated by reflections. „Ann. of Math.”. 35, s. 588–621, 1934. 
• Harold Scott MacDonald Coxeter. The groups determinated by the relations of the form ${\displaystyle R_{i}^{2}=(R_{i}R_{j})^{k_{ij}}=1}$. „J. London Math. Soc.”. 10, s. 21–25, 1935. 
• Harold Scott MacDonald Coxeter, William Moser: Generators and relationsfor discrete groups. Berlin Heidelberg New York: Springer Verlag, 1972.
• Nicolas Bourbaki: Groupes et algebres de Lie. T. XXXIV (rozdz. IV-VI). Paris: Hermann, 1968.