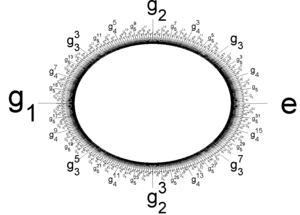
Grupa Prüfera

2-grupa Prüfera ${\displaystyle \langle g_{n}\colon g_{n+1}^{2}=g_{n},\ g_{1}^{2}=e\rangle .}$

Grupa Prüfera, p-grupa Prüfera a. grupa p-quasicykliczna – dla ustalonej liczy pierwszej p, wyznaczona jednoznacznie (z dokładnością do izomorfizmu) grupa torsyjna, w której każdy niezerowy element ma p pierwiastków p-tego stopnia. Nazwa pojęcia odnosi się do nazwiska niemieckiego matematyka Heinza Prüfera.

• p-grupa Prüfera może być reprezentowana jako podgrupa grupy okręgu jednostkowego ${\displaystyle \operatorname {U} (1)}$ jako zbiór wszystkich możliwych pierwiastków z jedynki stopnia ${\displaystyle p^{n}}$ przy ${\displaystyle n}$ przebiegającym wszystkie nieujemne liczby całkowite:

${\displaystyle \mathbb {Z} (p^{\infty })=\left\{e^{2\pi in/p^{m}}\colon n,m=1,2,3,\dots \right\}.}$

• Z drugiej strony p-grupę Prüfera można postrzegać jako p-podgrupę Sylowa grupy ${\displaystyle \mathbb {Q} /\mathbb {Z} }$ składającą się ze wszystkich elementów rzędu wyrażającego się jako potęga ${\displaystyle p{:}}$

${\displaystyle \mathbb {Z} (p^{\infty })=\mathbb {Z} [1/p]/\mathbb {Z} .}$

• Istnieje następująca prezentacja p-grupy Prüfera (w zapisie addytywnym):

${\displaystyle \mathbb {Z} (p^{\infty })=\langle x_{1},x_{2},\dots \colon px_{1}=0,px_{2}=x_{1},px_{3}=x_{2},\dots \rangle .}$

• p-grupa Prüfera jest jedyną (z dokładnością do izomorfizmu) nieskończoną p-grupą, która jest grupą lokalnie cykliczna (dowolny podzbiór skończony grupy generuje grupę cykliczną). Innymi słowy p-grupa jest p-grupą Prüfera wtedy i tylko wtedy, gdy jej każda podgrupa właściwa jest cykliczna oraz dla każdej liczby naturalnej ${\displaystyle k}$ istnieje w niej podgrupa rzędu ${\displaystyle p^{k}.}$

• p-grupa Prüfera jest podzielna.

• p-grupy Prüfera, dla wszystkich liczb pierwszych p, są jedynymi grupami nieskończonymi, których podgrupy są liniowo uporządkowane przez inkluzję. Ponieważ p-grupy Prüfera nie zawierają podgrup maksymalnych, to są one swoimi własnymi podgrupami Frattiniego. Poniższy ciąg zawierań przedstawia p-grupę Prüfera jako granicę prostą swoich podgrup skończonych:

${\displaystyle \{0\}\subset \mathbb {Z} /p\subset \mathbb {Z} /p^{2}\subset \mathbb {Z} /p^{3}\subset \dots \subset \mathbb {Z} (p^{\infty }).}$

• W teorii lokalnie zwartych grup topologicznych p-grupa Prüfera (wyposażona w topologię dyskretną) jest sprzężona w sensie Pontriagina do grupy zwartej p-adycznych liczb całkowitych, odwrotnie: p-grupa Prüfera jest sprzężeniem w sensie Pontryagina grupy p-adycznych liczb całkowitych^[1].

• Jako ${\displaystyle \mathbb {Z} }$-moduł p-grupa Prüfera jest modułem artinowskim, lecz nie noetherowskim; podobnie jako grupa: jest ona artinowska, ale nie noetherowska (podgrupy grupy abelowej są abelowe i pokrywają się z odpowiednimi podmodułami tej grupy traktowanej jako ${\displaystyle \mathbb {Z} }$-moduł). Ten fakt może służyć jako kontrprzykład na to, iż nie każdy moduł artinowski jest zarazem noetherowski (choć każdy pierścień artinowski jest noetherowski).

Zobacz też

• p-adyczne liczby całkowite, które można zdefiniować jako granicę odwrotną skończonych podgrup p-grup Prüfera
• diadyczne liczby wymierne, czyli liczby wymierne postaci ${\displaystyle a/2^{b};}$ 2-grupę Prüfera można postrzegać jako diadyczne liczby wymierne modulo 1

Przypisy

Bibliografia

• Nathan Jacobson: Basic algebra. Wyd. II. T. 2. Dover, 2009. ISBN 978-0-486-47187-7.
• Quasicyclic group na PlanetMath (ang.)
• N.N. Vil’yams: Quasi-cyclic group. Michiel Hazewinkel (red.). w: Encyclopaedia of Mathematics Kluwer Academic Publishers, 2001. ISBN 978-1556080104. (ang.)Sprawdź autora:1.