Hipocykloida

Hipocykloida – krzywa płaska, jaką zakreśla ustalony punkt okręgu toczącego się bez poślizgu wewnątrz okręgu o większym promieniu. Krzywa ta jest szczególnym przypadkiem hipotrochoidy.

Kształt hipocykloidy (liczba ostrzy) zależy od ilorazu ${\displaystyle {\tfrac {R}{r}}}$ promieni okręgów, nieruchomego do toczącego się.

Opis matematyczny

Hipocykloidę najłatwiej opisać równaniami parametrycznymi^[1]:

${\displaystyle x=(R-r)\cos(t)+r\cos \left({\frac {R-r}{r}}\,t\right),}$

${\displaystyle y=(R-r)\sin(t)-r\sin \left({\frac {R-r}{r}}\,t\right).}$

Przykłady

Asteroida jako ewoluta elipsy

Poniższe rysunki pokazują kilka hipocykloid dla różnych wartości ilorazów ${\displaystyle {\tfrac {R}{r}}}$

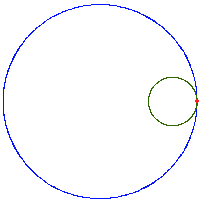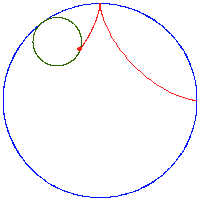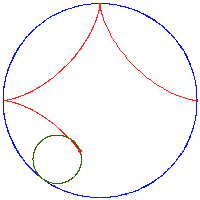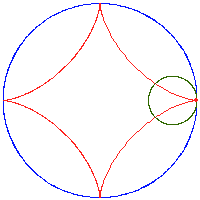
• hipocykloida ${\displaystyle {\tfrac {R}{r}}=3}$ (zwana też deltoidą) – powstawanie i krzywa statycznie:

(c) WojciechSwiderski, CC-BY-SA-3.0

• hipocykloida ${\displaystyle {\tfrac {R}{r}}=4}$ (zwana też asteroidą^[1]) – powstawanie i krzywa statycznie:

(c) WojciechSwiderski, CC-BY-SA-3.0

• dla ${\displaystyle {\tfrac {R}{r}}=2}$ hipocykloida redukuje się do średnicy dużego okręgu – fakt ten jest znany jako twierdzenie Kopernika i może być wykorzystany do zamiany ruchu obrotowego na posuwisto-zwrotny:

(c) WojciechSwiderski, CC-BY-SA-3.0

Jeżeli stosunek ${\displaystyle {\tfrac {R}{r}}}$ jest liczbą niewymierną, hipocykloida jest linią otwartą, a zbiór jej wierzchołków jest gęstym podzbiorem okręgu. Poniższe rysunki przedstawiają taką sytuację z tym, że parametr ${\displaystyle t}$ przebiega skończony przedział, [−10, 100] oraz [−10, 1000]:

Zobacz też

• cykloida
• epicykloida
• lista krzywych

Przypisy

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Hypocycloid, [w:] MathWorld [online], Wolfram Research [dostęp 2020-12-12]  (ang.).