Interpolacja trygonometryczna

Interpolacja trygonometryczna – metoda przybliżania funkcji za pomocą wielomianu trygonometrycznego (szeregu Fouriera). Taka interpolacja daje szczególnie dobre rezultaty przy przybliżaniu funkcji okresowych^[1], gdyż metody używające klasycznych wielomianów, pozbawionych okresowości, powodują duże błędy interpolacji.

Przypadkiem szczególnym jest sytuacja, gdy punkty węzłowe są równoodległe. W takim przypadku najlepszym rozwiązaniem jest dyskretna transformata Fouriera.

Metoda ogólna

Opracowano na podstawie materiału źródłowego^[1].

Założeniem każdej interpolacji jest spełnienie warunków: ${\displaystyle f(x_{k})=y_{k}\,\quad k=0,1,\dots ,(n-1)}$ gdzie:

${\displaystyle x_{k}=k\cdot {\frac {2\pi }{n}}\quad k=0,1,\dots ,(n-1).}$

Wtedy:

• Dla nieparzystej ilości ${\displaystyle n}$ punktów węzłowych:

${\displaystyle m={\frac {n-1}{2}},}$

${\displaystyle \Theta (x)={\frac {A_{0}}{2}}+\sum _{k=1}^{m}[A_{k}\cdot \cos(k\cdot x)+B_{k}\cdot \sin(k\cdot x)].}$

• Dla parzystej ilości ${\displaystyle n}$ punktów węzłowych:

${\displaystyle m={\frac {n}{2}},}$

${\displaystyle \Theta (x)={\frac {A_{0}}{2}}+\sum _{k=1}^{m-1}[A_{k}\cdot \cos(k\cdot x)+B_{k}\cdot \sin(k\cdot x)]+{\frac {A_{m}}{2}}\cdot \cos(m\cdot x).}$

• Dla obu powyższych przypadków:

${\displaystyle A_{j}={\frac {2}{n}}\sum _{k=0}^{n-1}[f(x_{k})\cdot \cos(j\cdot x_{k})],}$

${\displaystyle B_{j}={\frac {2}{n}}\sum _{k=0}^{n-1}[f(x_{k})\cdot \sin(j\cdot x_{k})].}$

Przykład

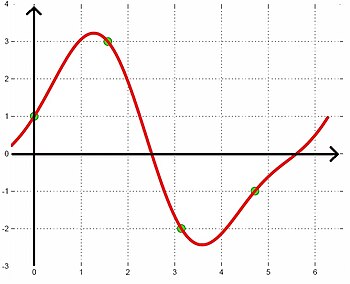
Punkty węzłowe z przykładu i funkcja interpolująca ${\displaystyle \Theta (x)}$ przez nie przechodząca

Dokonać interpolacji punktów za pomocą wielomianu trygonometrycznego:

${\displaystyle {\begin{array}{|c||cccc|}k&0&1&2&3\\f_{k}&1&3&-2&-1\end{array}}.}$

Rozwiązanie

Ilość punktów interpolowanych: ${\displaystyle n=4}$ (parzyste)

Stopień: ${\displaystyle m={\frac {n}{2}}=2}$

${\displaystyle x_{k}=k\cdot {\frac {2\pi }{4}}\Rightarrow x_{k}=\left\{0,\ {\frac {\pi }{2}},\ \pi ,\ {\frac {3}{2}}\pi \right\}}$

${\displaystyle A_{0}={\frac {2}{n}}\sum \limits _{k=0}^{n-1}f_{k}\cdot \cos(0\cdot x_{k})={\frac {2}{4}}\sum \limits _{k=0}^{3}f_{k}\cdot \cos(0\cdot x_{k})={\frac {1}{2}}(1\cdot 1+3\cdot 1-2\cdot 1-1\cdot 1)={\frac {1}{2}}}$

${\displaystyle A_{1}={\frac {2}{4}}\sum \limits _{k=0}^{3}f_{k}\cdot \cos(1\cdot x_{k})={\frac {1}{2}}\left[1\cdot \cos(0)+3\cdot \cos \left({\frac {\pi }{2}}\right)-2\cdot \cos(\pi )-1\cdot \cos \left({\frac {3}{2}}\pi \right)\right]={\frac {3}{2}}}$

${\displaystyle A_{2}={\frac {2}{4}}\sum \limits _{k=0}^{3}f_{k}\cdot \cos(2\cdot x_{k})={\frac {1}{2}}[1\cdot \cos(0)+3\cdot \cos(\pi )-2\cdot \cos(2\pi )-1\cdot \cos(3\pi )]=-{\frac {3}{2}}}$

${\displaystyle B_{0}={\frac {2}{n}}\sum \limits _{k=0}^{n-1}f_{k}\cdot \sin(0\cdot x_{k})=0}$

${\displaystyle B_{1}={\frac {2}{4}}\sum \limits _{k=0}^{n-1}f_{k}\cdot \sin(1\cdot x_{k})={\frac {1}{2}}[1\cdot 0+3\cdot 1-2\cdot 0-1\cdot (-1)]=2}$

${\displaystyle B_{2}={\frac {2}{n}}\sum \limits _{k=0}^{n-1}f_{k}\cdot \sin(2\cdot x_{k})=0}$

Odpowiedź

${\displaystyle \Theta (x)={\frac {1}{4}}+A_{1}\cdot \cos(x)+B_{1}\cdot \sin(x)+{\frac {A_{2}}{2}}\cdot \cos(2x)={\frac {1}{4}}+{\frac {3}{2}}\cos(x)+2\sin(x)-{\frac {3}{4}}\cos(2x)}$

Wielomian zespolony

Problem staje się bardziej naturalny jeśli sformujemy go w dziedzinie zespolonej. Możemy wtedy zapisać zależność na wielomian trygonometryczny w postaci:

${\displaystyle p(x)=\sum _{m=-n}^{n}c_{m}e^{imx},}$

gdzie i jest wielkością urojoną. Jeśli założymy, że ${\displaystyle z=e^{ix},}$ wtedy

${\displaystyle p(z)=\sum _{m=-n}^{n}c_{m}z^{m}.}$

Redukuje to problem interpolacji trygonometrycznej do interpolacji wielomianowej na okręgu jednostkowym. Dowód i jednoznaczność interpolacji trygonometrycznej staje się więc wtedy równoważnym odpowiednim założeniom dla interpolacji wielomianowej^[2].

Zobacz też

• aproksymacja
• interpolacja

Przypisy