Inwersja (geometria)
Inwersja – rodzaj przekształcenia geometrycznego; można je sobie wyobrażać jako „wywinięcie” wnętrza ustalonego koła na zewnątrz i „zawinięcie” zewnętrza tego koła do jego wnętrza. Do kluczowych własności inwersji należą: zachowywanie kątów (nieskierowanych) oraz fakt, iż obrazami uogólnionych okręgów (tzn. okręgów lub prostych interpretowanych jako okręgi o nieskończonym promieniu) są uogólnione okręgi. Pojęcie to uogólnia się na przestrzenie wyższego wymiaru, zob. Uogólnienia.
Choć inwersje można zdefiniować dla płaszczyzny euklidesowej (lub ogólniej: afinicznej), to naturalnym miejscem badania tych przekształceń jest płaszczyzna inwersyjna rozszerzająca płaszczyznę o nienależący do niej punkt nazywany punktem w nieskończoności (nieskończenie dalekim, niewłaściwym, idealnym). Dodanie punktu do liczb zespolonych (zob. uzwarcenie) daje zespoloną prostą rzutową nazywaną często sferą Riemanna.
Definicja
Inwersją względem okręgu nazywa się przekształcenie płaszczyzny euklidesowej spełniające warunki[1]:
oraz
Na płaszczyźnie inwersyjnej dodaje się jeszcze dwa warunki, dzięki którym przekształcenie inwersyjne jest określone dla wszystkich jej punktów:
Własności
Punktami stałymi inwersji są punkty okręgu inwersyjnego. Ponadto przekształca ona uogólnione okręgi (okręgi i proste) na uogólnione okręgi, dokładniej:
- Przekształca proste nieprzechodzące przez środek okręgu inwersyjnego na okręgi przechodzące przez środek okręgu inwersyjnego (i na odwrót); odwzorowuje w siebie proste przechodzące przez środek okręgu inwersyjnego.
- Odwzorowuje okręgi nieprzechodzące przez środek okręgu inwersyjnego na okręgi nieprzechodzące przez środek okręgu inwersyjnego; uogólniony okrąg przechodzi w siebie wtedy i tylko wtedy, gdy jest prostopadły do okręgu inwersyjnego w ich punktach przecięcia.
Wymienione przekształcenia można odwrócić, gdyż inwersja jest inwolucją. Dodatkowo inwersje są odwzorowaniami wiernokątnymi, tzn. zachowują kąty między krzywymi (w szczególności: prostymi i okręgami), lecz zmieniają znak miary kątów skierowanych (są antykonforemne).
Złożenie dwóch inwersji względem współśrodkowych okręgów o promieniach jest złożeniem dwóch jednokładności o skali
Odwrotność zespolona
Ponieważ punktowi płaszczyzny można przypisać liczbę zespoloną to można zdefiniować inwersję względem okręgu jednostkowego za pomocą odwrotności gdzie oznacza sprzężenie liczby
Odwrotność zespolona jest obok przesunięć równoległych i obrotów generatorem grupy Möbiusa. To właśnie odwrotność nadaje osobliwy ton geometrii Möbiusa utożsamianej czasem z geometrią inwersyjną (płaszczyzny euklidesowej). Geometria inwersyjna jest bogatsza niż geometria Möbiusa, gdyż operuje się w nim odwzorowaniem inwersyjnym nieprzekształconym poprzez sprzężenie w odwrotność. W ten sposób zawiera ona także sprzężenie, z kolei grupa Möbiusa nie zawiera ani sprzężenia, a co za tym idzie inwersji względem okręgu, gdyż nie są one konforemne (elementami tej grupy są funkcje analityczne płaszczyzny, które są konforemne).
Uogólnienia
Inwersja względem okręgu uogólnia się na inwersję względem sfery w przestrzeni trójwymiarowej mutatis mutandis. Podobnie jak w przypadku dwuwymiarowym obrazem inwersyjnym sfery jest sfera, ale gdy przechodzi ona przez środek sfery inwersyjnej, to jest ona przekształcana w płaszczyznę; dowolna płaszczyzna nie przechodząca przez środek sfery inwersyjnej jest przekształcana w inwersji na sferę zawierającą środek sfery inwersyjnej.
Rzut stereograficzny to przypadek szczególny inwersji sfery. Niech dana będzie sfera o promieniu jednostkowym i płaszczyzna styczna z w biegunie południowym sfery Wówczas jest rzutem stereograficznym względem bieguna północnego sfery Inwersja względem sfery o promieniu 2 i środku przekształca na jej rzut stereograficzny
Geometria inwersyjna służy badaniu przekształceń generowanych przez przekształcenia euklidesowe wraz z inwersją względem -sfery,
gdzie oznacza promień inwersji. Na płaszczyźnie, dla powyższy wzór opisuje inwersję względem okręgu jednostkowego.
Odwzorowania konforemne przestrzeni wyższych wymiarów można opisać jako złożenia inwersji względem hipersfer lub hiperpłaczyzn oraz ruchów euklidesowych, o czym mówi twierdzenie Liouville'a o odwzorowaniach konforemnych.
Przypisy
- ↑ Inwersja, [w:] Encyklopedia PWN [online] [dostęp 2021-07-21].
Linki zewnętrzne
- Inwersje kwadratu, koła oraz pęku prostych i okręgów względem okręgu na YouTube
- Inwersja trójwymiarowego modelu konia względem sfery na YouTube
Media użyte na tej stronie
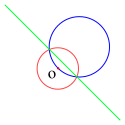
Autor: CheCheDaWaff, Licencja: CC BY-SA 4.0
An illustration of in the inverse of a circle with respect to a circle it does not pass through the centre of.
Autor: Krishnavedala, Licencja: CC BY-SA 3.0
P' is the inverse of P with respect to the circle.
Autor: CheCheDaWaff, Licencja: CC BY-SA 4.0
An illustration of the inverse of a circle with respect to a circle it passes through the centre of.