Koło zębate

Przykłady kół zębatych o zębach prostych i śrubowych

Koło zębate – element czynny przekładni zębatej oraz element innych mechanizmów takich jak sprzęgło zębate, pompa zębata i innych.

W skład koła zębatego wchodzą:

• wieniec zębaty
• piasta
• łącznik (łączący piastę i wieniec)^[1].

W niektórych kołach zębatych, szczególnie tych o niewielkiej liczbie zębów i małej średnicy, nie występuje łącznik, a wieniec zębaty spełnia jednocześnie rolę piasty. Takiego rodzaju koło zębate nazywa się zębnikiem. Zębnik często nacięty jest bezpośrednio na wale i tworzy z nim integralną całość^[2] lub osadzony jest na nim za pomocą połączenia wciskowego^[3].

Wieniec zębaty składa się z zębów i wieńca, z którego zęby wystają. Przestrzenie pomiędzy zębami nazywane są wrębami^[4].

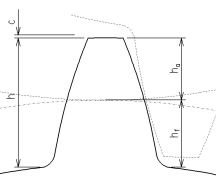
Parametry koła zębatego

(c) Jonasz, CC-BY-SA-3.0

Parametry koła zębatego i zębów

(c) Jonasz, CC-BY-SA-3.0

Ząb koła zębatego

${\displaystyle z}$ – liczba zębów

${\displaystyle d}$ – średnica podziałowa

średnica okręgu, na którym szerokość wrębu jest równa grubości zęba

${\displaystyle d_{a}}$ – średnica wierzchołkowa

średnica okręgu przechodzącego przez wierzchołki zębów

${\displaystyle d_{f}}$ – średnica stóp

średnica okręgu przechodzącego przez dna wrębów

${\displaystyle d_{b}}$ – średnica koła zasadniczego

średnica wyobrażalnego koła, z którego rozwijane są zarysy ewolwentowe boków zębów

${\displaystyle p}$ – podziałka obwodowa

odległość jednoimiennych boków zębów mierzona na łuku koła podziałowego

${\displaystyle p_{b}}$ – podziałka zasadnicza

podziałka mierzona wzdłuż łuku koła zasadniczego

${\displaystyle m}$ – moduł zęba

parametr charakteryzujący wielkość zębów koła zębatego. Moduły kół współpracujących muszą być takie same. Moduł zęba jest wielkością znormalizowaną przez Polską Normę PN/M-88502. Oblicza się go ze wzoru ${\displaystyle m=p\div \Pi }$

${\displaystyle h}$ – wysokość zęba

suma wysokości głowy i stopy zęba

${\displaystyle h_{a}}$ – wysokość głowy zęba

${\displaystyle h_{f}}$ – wysokość stopy zęba

${\displaystyle y}$ – współczynnik wysokości zęba

wysokość głowy zęba wyrażona w krotności modułu

${\displaystyle y=1}$ zęby normalne stosowane w większości przekładni zębatych

${\displaystyle y<1}$ zęby niskie stosuje się w przekładniach zębatych stożkowych o zębach łukowych, w których koło małe ma niewielką liczbę zębów (od 5 do 10), w przekładniach ślimakowych, w sprzęgłach zębatych, w ewolwentowych połączeniach wielowypustowych

${\displaystyle y>1}$ zęby wysokie stosowane w pompach zębatych.

${\displaystyle x}$ – współczynnik korekcji

przesunięcie zarysu odniesienia przy wykonywaniu koła zębatego wyrażone w krotności modułu

${\displaystyle x=0}$ koło niekorygowane

${\displaystyle x>0}$ odsunięcie zarysu odniesienia np. dla uniknięcia podcinania zębów

${\displaystyle x<0}$ dosunięcie zarysu odniesienia^[4]

${\displaystyle c}$ – luz wierzchołkowy

zwykle 0,2–0,25 modułu^[5]

Kształt linii zęba

• zęby proste
• zęby śrubowe
• zęby daszkowe (w przekładniach walcowych)
• zęby krzywoliniowe (w przekładniach stożkowych)^[4]

Mechanika zazębienia

(c) Jonasz, CC-BY-SA-3.0

Schemat mechaniki zazębienia

Animacja zazębienia

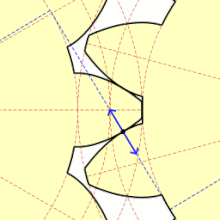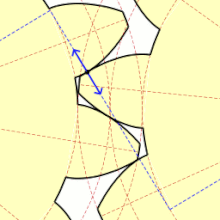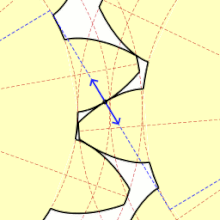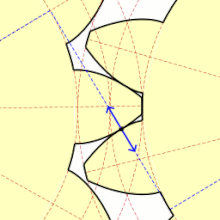
Podczas obrotu kół dwa współpracujące zęby otaczają się jednocześnie także ślizgając się po sobie. Ten poślizg jest niekorzystnym, lecz niemożliwym do uniknięcia zjawiskiem. Tylko w bardzo wąskim zakresie, który teoretycznie sprowadza się do jednego punktu ${\displaystyle C,}$ występuje czyste toczenie się zębów bez poślizgu. Punkt ten nazywa się punktem tocznym, który wyznacza koło toczne o średnicy ${\displaystyle d_{w}.}$ Koła toczne dla obu współpracujących kół są styczne w punkcie ${\displaystyle C.}$

Punkty styku zębów w czasie obrotu układają się na odcinku (${\displaystyle E_{1},}$ ${\displaystyle E_{2}}$) zwanym odcinkiem przyporu. Kąt ${\displaystyle \alpha }$ zawarty między tym odcinkiem a linią styczną do kół tocznych w punkcie tocznym jest zwany kątem przyporu i jest jednocześnie parametrem ewolwenty. Zarys nominalny, powszechnie używany w budowie maszyn i przyjęty przez praktycznie wszystkie normy na całym świecie ma kąt przyporu ${\displaystyle \alpha =20^{\circ }}$ Jednocześnie dla zarysu nominalnego średnice podziałowe kół pokrywają się z kołami tocznymi^[4].

Obliczenia wytrzymałościowe

Ze względu na złożoność zjawisk zachodzących w uzębieniu niemożliwe jest stworzenie analitycznej metody obliczania wytrzymałości zęba. Tradycyjnie stosowane są tu metody parametryczne, które pozwalają uwzględnić szereg parametrów pracy przekładni takich jak – przenoszona moc, prędkość kół, wielkość, przełożenia, liczba zębów, intensywność pracy, rodzaj smarowania oraz chłodzenia itp. parametry związane są empirycznymi formułami i w ostateczności pozwalają na obliczenie minimalnego wymaganego modułu zęba.

Współczesna technologia dostarcza komputerowych metod modelowania zjawisk wewnątrz obciążonych części maszyn, także i kół zębatych, co znacznie ułatwia przeprowadzenie ewaluacji konstrukcji.

Szczególnym przypadkiem kół zębatych są:

• koła w kształcie owalu albo serca stosowane w przekładniach o przełożeniu zmiennym w czasie każdego obrotu, które mimo odmiennego kształtu są nazywane kołami zębatymi
• koła przekładni łańcuchowej o zmiennym przełożeniu składające się z ruchomych segmentów
• wycinek koła stosowany w przekładniach o niepełnym obrocie np. w mechanizmie podniesienia działa.

Obliczenia wytrzymałościowe dla koła zębatego walcowego prostego:

1. Obliczenie modułu z warunku na zginanie
2. Obliczenie modułu z warunku na naciski powierzchniowe
3. Dobór modułu według tablicy
4. Obliczenie pozostałych parametrów koła zębatego

Obliczenia

0. Zaczynamy od określenia danych wstępnych: ${\displaystyle n_{1},z_{1},u,M{:}}$

${\displaystyle u}$ – przełożenie,

${\displaystyle M_{o}={\tfrac {M\cdot K_{p}\cdot K_{v}}{K_{e}}},}$

gdzie:

${\displaystyle K_{v}=1{,}25{\text{–}}2{,}3}$ (współczynnik nadwyżek dynamicznych, zależy od prędkości obwodowej koła),

${\displaystyle K_{e}=1}$ lub ${\displaystyle K_{e}=2}$ (współczynnik zależny od liczby przyporu),

${\displaystyle K_{p}=1{\text{–}}2}$ (współczynnik przeciążenia zależny od warunków pracy).

1. Moduł z warunku na zginanie:

${\displaystyle m\geqslant {\sqrt[{3}]{\tfrac {2M_{o}\cdot q}{\lambda \cdot z_{1}\cdot k_{gj}}}},}$

${\displaystyle v=100\cdot {\tfrac {\pi \cdot d_{1}\cdot n}{60}},}$

${\displaystyle d_{1}=z_{1}\cdot m}$ – średnica podziałowa,

${\displaystyle b=\lambda \cdot m}$ – szerokość wieńca,

gdzie:

${\displaystyle q,}$ ${\displaystyle \lambda ,}$ ${\displaystyle k_{gj}}$ – z tablic.

2. Obliczanie zębów na naciski powierzchniowe:

${\displaystyle p_{max}={\sqrt {2/(1/E_{1}+1/E_{2})\cdot \Pi \cdot \sin \alpha \cdot \cos \alpha }}\cdot {\sqrt {F/(b\cdot d)\cdot 1\pm 1/i}},}$

gdzie:

${\displaystyle E_{1},}$ ${\displaystyle E_{2}}$ – moduły Younga materiałów uzębień w MPa,

${\displaystyle \alpha }$ – kąt przyporu,

${\displaystyle F}$ – siła nacisku kół na siebie,

${\displaystyle b}$ – tzw. czynna szerokość uzębienia (grubość koła) w mm,

${\displaystyle i}$ – przełożenie^[4].

Obróbka uzębień

Frezowanie obwiedniowe frezem ślimakowym

Występuje wiele metod kształtowania uzębień^[6][7] kół zębatych wykonanych z metalu:

• kształtowe
  • frezowanie frezem modułowym krążkowym
  • frezowanie frezem palcowym
  • dłutowanie
  • struganie
  • przeciąganie
  • wycinanie elektroerozyjne (obróbka elektroerozyjna – WEDM)
• kopiowe
  • struganie według kopiału
• obwiedniowe
  • dłutowanie metodą Maaga
  • dłutowanie metodą Fellowsa
  • struganie metodą Sunderlanda
  • frezowanie obwiedniowe frezem ślimakowym walcowym lub globoidalnym
  • frezowanie frezem ślimakowym stożkowym
  • frezowanie głowicą frezową z zębami ustawionymi według okręgu
  • frezowanie głowicą frezową z zębami ustawionymi według spirali (spiral) Archimedesa

Koła zębate z tworzyw sztucznych wykonywane są głównie metodą wtryskiwania.

Przypisy