Kropla

Krople wody

Odrywanie się kropli

Fala na wodzie po kapnięciu kropli

Rozprysk kropli po upadku na twardą powierzchnię

Kropla – ciało ciekłe, zazwyczaj małej objętości, ograniczone w całości lub większości powierzchnią swobodną. Przykładem są krople deszczu, rosy lub tłuszczu w śmietanie.

Z wyjątkiem miejsc styku kropli z dwiema różnymi substancjami, powierzchnia swobodna kropli jest zbliżona do sfery. W warunkach naturalnych na Ziemi, kropla wody spadająca w powietrzu może mieć średnicę do kilku milimetrów. Chmury składają się w większości z kropel o rozmiarach rzędu kilku mikrometrów. W terminach stosowanych w meteorologii, większe krople wody nazywa się deszczowymi, a mniejsze chmurowymi. Krople mogą w odpowiednich warunkach mieć niemal dowolne wymiary. Szczególnie łatwo jest wytworzyć duże krople z cieczy w stanie nieważkości^[1].

Decydujący wpływ na kształt powierzchni swobodnej kropli mają siły napięcia powierzchniowego powstające wskutek oddziaływań międzycząsteczkowych. Kropla w stanie swobodnym, gdy nie działają na nią żadne siły zewnętrzne lub siły te się znoszą, przybiera kształt idealnej kuli, gdyż jest to bryła o najmniejszej możliwej powierzchni. Na kształt kropli wpływ mają też inne oddziaływania zewnętrzne i wewnętrzne, a także wzbudzone fale. Często powoduje to, że kształt kropli znacznie odbiega od kulistego, co dotyczy zwłaszcza kropel znajdujących się na powierzchni ciał stałych oraz dużych kropel w atmosferze.

Powstawanie

Krople w laboratorium wytwarza się poprzez wolny wypływ cieczy z pionowej rurki o małej średnicy, gdy formująca się wisząca kropla przekroczy określoną wielkość. Zjawisko to jest stosowane w praktyce we wkraplaczach, biuretach i pipetach. Tę metodę wykorzystuje się również w polarografii prowadzonej na kroplowej (kapiącej) elektrodzie rtęciowej. Krople powstają też przez rozpad strumienia cieczy wskutek zawirowań wewnętrznych lub drgań na granicy ciecz-powietrze. Zawirowania i fale w cieczy oraz otaczającym je ośrodku zmniejszają wielkość kapiących kropel.

Wytwarzanie kropel o odpowiedniej średnicy wymaga malowanie rozpryskowe, wykonywanie oprysku roślin w rolnictwie i ogrodnictwie. Drukarki atramentowe nanoszą tusz na papier poprzez wystrzeliwanie malutkich kropel środka barwiącego przez mikroskopijne dysze znajdujące się w głowicy drukarki przechodzącej nad zadrukowywaną powierzchnią.

Małe krople chmurowe powstają poprzez kondensację pary wodnej zawartej w atmosferze, a znacznie większe krople deszczowe przez proces koagulacji (zderzania się i zlewania kropli chmurowych) lub przez proces kondensacyjny z udziałem kryształów lodu i kropel wody. Proces ten jest złożony, zajmuje się nim dział meteorologii zwany mikrofizyką chmur.

Własności fizyczne i znaczenie

Etapy formowania się kropli

Formująca się kropla, wypływająca z pionowej rurki, jest przyciągana przez siły ciężkości, a utrzymywana przez siły napięcia powierzchniowego, jednocześnie gdy kropla rośnie powstaje przewężenie ze zmniejszającą się średnicą. Po oderwaniu się kropli siły lepkości tłumią powstałą na jej powierzchni falę, a siły napięcia powierzchniowego formują bryłę o jak najmniejszej powierzchni przy danej objętości – kulę.

Dla danej średnicy rurki wielkość kropli odrywającej się od rurki zależy od napięcia powierzchniowego cieczy. Własność ta jest wykorzystywana do odmierzania cieczy lub w warunkach laboratoryjnych do wyznaczania napięcia powierzchniowego cieczy za pomocą stalagmometru.

Zastosowano je w zaliczanym do jednego z najpiękniejszych eksperymentów fizycznych doświadczalnym wyznaczeniu ładunku elektronu, przeprowadzonym przez R. Millikana.

Krople wody znajdujące się w atmosferze nazwane są mgłą, zamgleniem, chmurą, deszczem w zależności od wielkości kropel i ich koncentracji. Na kroplach wody tworzą się różnego rodzaju zjawiska optyczne, takie jak tęcza. Tęcza powstaje w wyniku załamania i odbicia światła w kropli wody w powietrzu, a szczególnie jest efektem zależności współczynnika załamania światła dla wody od długości fali świetlnej.

Ciśnienie w kropli

Siły napięcia powierzchniowego sprawiają, że w kropli panuje większe ciśnienie niż na zewnątrz, ciśnienie to określa wzór:

${\displaystyle P_{I}=P_{O}+{\frac {2\gamma }{R}},}$

gdzie:

${\displaystyle P_{I}}$ – ciśnienie w kropli,

${\displaystyle P_{O}}$ – ciśnienie zewnętrzne,

${\displaystyle \gamma }$ – napięcie powierzchniowe,

${\displaystyle R}$ – promień kropli.

Przykładowo dla kropli wody o średnicy 1 nanometra przyrost jest teoretycznie równy 170 MPa, czyli około 1700 atm. Kropla o średnicy 1 nanometra jest jednak tworem czysto teoretycznym, gdyż pojedyncza cząsteczka wody zajmuje objętość ok. 0,03 nanometra sześciennego, zatem kropla o takiej średnicy składałaby się z około 18 cząsteczek. Można uznać, że na jej powierzchni jest około 10 cząsteczek. Przy takiej skali trudno mówić o kulistej powierzchni i jednakowym ciśnieniu, większy wpływ na jej własności mają zjawiska związane z pojedynczymi cząsteczkami w tym i zjawiska kwantowe, a nie makroskopowe.

Zależność kształtu kropli od jej wielkości.

Kształt

Krople swobodnie spadające w powietrzu

Na temat kształtu spadającej kropli potocznie istnieją m.in. poniższe błędne poglądy:

• kropla ma kształt wydłużony w pionie, z „ogonkiem” na górze,
• przyciąganie ziemskie wydłuża kroplę,
• kropla przyjmuje najlepszy pod względem aerodynamicznym kształt.

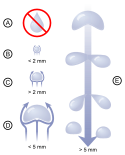
W rzeczywistości siły napięcia powierzchniowego sprawiają, że swobodnie spadające krople o średnicy do 1 mm mają kształt niemal doskonale kulisty. Znajdują się one w jednorodnym polu grawitacyjnym, a więc nie deformuje ono kształtu kropel. W przypadku spadania w powietrzu są one deformowane przez siłę aerodynamiczną – krople rozszerzają się i spłaszczają, te o średnicy powyżej 2 mm są wyraźnie spłaszczone.

Im większa jest kropla, tym prędkość jej spadania w powietrzu jest większa, a ze względu na większy promień siły napięcia powierzchniowego odgrywają coraz mniejszą rolę. Dla kropel o średnicy większej niż około 3 milimetry powstaje u dołu kropli wgłębienie, a kształt przekroju kropli jest zbliżony do przekroju ziarna fasoli, przy promieniu około 5 mm wgłębienie jest tak duże, że kropla na środku staje się cienka. Kropla taka jest niestabilna i niewielkie zaburzenie sprawia, że rozpada się na mniejsze krople^[2][3].

Deformacje kształtu można analizować, stosując równanie Bernoulliego. Najszybszy przepływ powietrza, względem kropli, jest z boku kropli, a tam gdzie jest najszybszy przepływ, tam też jest najmniejsze ciśnienie gazu. Zmniejszenie ciśnienia określa zależność ${\displaystyle dp=-0{,}5\rho v^{2}.}$

Krople stykające się z ciałem stałym

Kropla na powierzchni ciała stałego w zależności od kąta zwilżania

Krople wody spływające po liściu

Ciecz, stykając się z ciałem stałym, może rozpływać się po całej jego powierzchni lub tworzyć krople przylegające do niego. Na granicy styku cieczy, ciała stałego i gazu ciecz tworzy zawsze taki sam kąt z powierzchnią ciała stałego, który nazywa się kątem zwilżania. Kropla przylegająca do powierzchni tworzy kształt odpowiadający minimum energii wszystkich sił działających na nią:

• przyciągania ziemskiego (najistotniejsza),
• powierzchniowej ciała stałego,
• napięcia powierzchniowego cieczy.

W zależności od warunków krople mogą przybierać kształt najczęściej spłaszczonej elipsoidy^[4] lub rzadziej wycinka kuli.

Przykładem cieczy o bardzo dużym napięciu powierzchniowym jest rtęć, jej powierzchnia styku z większością materiałów jest bardzo mała, kulki łatwo toczą się. Ciecze o małym napięciu powierzchniowym formują na powierzchni bardziej spłaszczone struktury zwane batonnetami^[5].

Na krople spływające po powierzchni ciał stałych silny wpływ ma też faktura i kształt tej powierzchni. Krople spływające bardzo rzadko miewają kształt zbliżony do kuli, są one dodatkowo deformowane przez niesymetryczność zjawiska przylegania (histereza adhezji), polegające na tym, że w miejscu napływania (dolegania) cieczy kąt zwilżania jest większy od statycznego, a w miejscu odpływania – mniejszy. Przy dużej prędkości spływu istotne znaczenia dla kształtu ma też tarcie wewnętrzne oraz dynamika płynu.

Spadanie kropli

Wpadnięcie kropli wody do wody

Kropla, w tym i kropla deszczu, spadając pod wpływem przyciągania ziemskiego doznaje oporu powietrza i już po kilku metrach przebytej drogi osiąga prędkość końcową. Dla małych liczb Reynoldsa prędkość końcowa spadania ciał o kształcie kuli określa prawo Stokesa, które daje dobre rezultaty tylko dla kropel o średnicy mniejszej niż 0,3 mm, natomiast dla większych stosuje się wzory aproksymujące dane eksperymentalne lub wynikające z rozwiązania pełnego równania Naviera-Stokesa. Przeprowadzone liczne pomiary prędkości spadania kropel deszczu pozwoliły stwierdzić, że prędkość końcowa kropel zależy w skomplikowany sposób od ich średnicy^[6][7].

(c) Ency z polskiej Wikipedii, CC BY-SA 2.5

Wykres dla prędkości końcowej kropli

Przyczyną niezgodności równania Stokesa dla dużych kropel jest wzrost ich prędkości przy wzroście średnicy. Wraz z prędkością rosną zaburzenia przepływu wokół kropli. Parametrem opisującym rodzaj przepływu jest liczba Reynoldsa. Drugim czynnikiem jest deformacja, zwiększająca powierzchnię poprzeczną kropli, a także zwiększająca turbulencje wokół kropli.

Zagadnieniem wyrażenia prędkości końcowej kropli empirycznym wzorem matematycznym zajmowało się wielu badaczy, a w wyniku ich prac zaproponowano szereg wzorów zależności prędkości końcowej kropli V w m/s od średnicy d w mm, jak poniższe dwa przykładowe wykorzystane w załączonym obok wykresie podającym też dane eksperymentalne:

${\displaystyle V=9{,}65(1-\exp(-0{,}53d),)}$ Gossard (1992),

${\displaystyle V=4{,}85d\exp(-0{,}195d),}$ Uplingers (1977).

Wzory można stosować dla kropel o średnicy do 6 mm, przy czym dla średnic do 1 mm oba wzory wykazują podobny przebieg, natomiast w przedziale 1 do 6 mm dokładniej rzeczywistość odwzorowuje wzór Uplingersa. Dla wartości powyżej 6 mm oba wzory dają wyniki coraz bardziej rozbieżne, ponadto i tak nie można ich zweryfikować empirycznie, gdyż krople takich rozmiarów są niestabilne w warunkach panujących na Ziemi. Z danych zebranych przez różnych autorów wynika, że wzory te nie opisują dobrze prędkości spadania kropel o średnicy mniejszej od 1 mm.

Prędkość poruszania się kropli w powietrzu odgrywa ważną rolę w meteorologii, gdyż radary dopplerowskie mierzą prędkość powietrza poprzez pomiar prędkości ruchu kropel, która różni się od prędkości ruchu powierza o szybkość spadania kropel. W pomiarach tych zakłada się, że krople dostosowują się natychmiast do zmian prędkości powietrza, w rzeczywistości kropla o średnicy 1 mm potrzebuje na to ok. 1–2 sekund. Istnieją jednak radary meteorologiczne, w których prędkość powietrza można oszacować na podstawie pomiaru odbicia fal od czystego nieba (rozproszonego na atomach).

Kropla jako jednostka objętości

Krople stosowane są jako pozaukładowe jednostki objętości:

• potocznie kroplą określa się najmniejszą możliwą do odmierzenia ilość cieczy, z tym że jej wielkość zależy od przyrządu lub obiektu służącego do otrzymania
• w gospodarstwie domowym przyjmuje się, że objętość kropli wynosi od 1/20 do 1/10 ml (50-100 μl)
• kropla imperialna – wynosi 1/288 imperialnej uncji płynu, czyli ok. 99 μl
• w USA kropla definiowana jest jako 1/60 lub 1/76 łyżeczki do herbaty, czyli ok. 82 μl lub 65 μl

Historia badań

Jednym z badaczy kropli w powietrzu był Philipp Lenard, który opublikował swe badania^[8] w 1904 roku.

Zobacz też

• krople
• model kroplowy jądra atomowego

Przypisy

Linki zewnętrzne

• Galeria kropli
• Fotometryczny model kropli deszczu
• Przekształcanie się strumienia płynu w krople