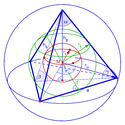
Kula wpisana

Czworościan foremny wraz z kulą wpisaną (czerwoną), opisaną (niebieską) oraz pośrednią (zieloną)

Kula wpisana w wielościan – kula, która mieści się cała w danym wielościanie i której powierzchnia dotyka wszystkich ścian wielościanu. O takim wielościanie można powiedzieć, że jest opisany na kuli^[1][2].

Powierzchnia kuli, a bardziej formalnie – jej brzeg, nazywana jest sferą. W definicji można zastąpić kulę pojęciem sfery nie zmieniając żywotnie jej sensu. Dlatego obok kuli wpisanej w wielościan, mówi się równoważnie o sferze wpisanej w wielościan (analogicznie do koła/okręgu wpisanego w wielokąt).

Twierdzenie mówiące, że jeżeli w wielościan można wpisać kulę, wszystkie odcinki łączące wierzchołek wielościanu z punktami styczności kuli do sąsiadujących ścian są równej długości, bywa określane jako „najmocniejsze twierdzenie stereometrii”^[3]. Znane jest też twierdzenie, że objętość takiego wielościanu jest równa jednej trzeciej iloczynu sumy pól ścian i promienia kuli wpisanej^[4].

Nie każdy wielościan można opisać na kuli. Można tego jednak dokonać między innymi dla każdego wielościanu foremnego, a także każdego wielościanu Catalana^[5]. Kulę wpisaną można zdefiniować także dla niektórych innych brył, jak chociażby stożek, stożek ścięty czy walec^[6]. Archimedes wykazał, że objętość kuli wpisanej w walec kołowy prosty (o wysokości równej średnicy podstawy) do którego wpisany jest także stożek (określający szerokość walca) są w stosunku objętości 1:2:3 (odpowiednio kula, stożek, walec)^[7], a jego rozumowanie zostało sformalizowane i uogólnione w XVIII wieku, dając początek zasadzie Cavalieriego^[8]. Według relacji Plutarcha szkic tego odkrycia znalazł się na grobie Archimedesa, zgodnie z wyrażonym przez uczonego życzeniem^[9]. Oprócz kuli wpisanej można również zdefiniować kulę opisaną oraz kulę pośrednią^[10].

Zobacz też

• koło wpisane
• sfera półwpisana

Przypisy