Kwadryka

Kwadryka lub powierzchnia drugiego stopnia – powierzchnia dana równaniem drugiego stopnia ze względu na współrzędne ${\displaystyle x,\ y,\ z}$^[1]:

${\displaystyle a_{11}x^{2}+a_{22}y^{2}+a_{33}z^{2}+2a_{12}xy+2a_{23}yz+2a_{13}zx+2a_{14}x+2a_{24}y+2a_{34}z+a_{44}=0,\qquad (1)}$

gdzie:

${\displaystyle a_{11},a_{22},a_{33},a_{12},a_{23},a_{13},a_{14},a_{24},a_{34},a_{44}\in \mathbb {R} ,}$

przy czym nie zachodzi

${\displaystyle a_{11}=a_{22}=a_{33}=a_{12}=a_{23}=a_{13}=0}$

(przynajmniej jeden z powyższych współczynników musi być różny od zera).

W zależności od wartości współczynników ${\displaystyle a_{ij}}$ kwadryka może należeć do jednego z wielu typów, różniących się właściwościami.

Wykresy i równania kanoniczne

Poprzez odpowiednie przekształcenie układu współrzędnych można równanie kwadryki sprowadzić do postaci kanonicznej, charakterystycznej dla jednego z wymienionych niżej 17 typów.

W poniższych wzorach ${\displaystyle a,b,c\in \mathbb {R} _{+}.}$

elipsoida	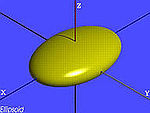${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1}$
elipsoida obrotowa     (szczególny przypadek elipsoidy)	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{a^{2}}}+{\frac {z^{2}}{b^{2}}}=1}$
sfera         (szczególny przypadek elipsoidy obrotowej)	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{a^{2}}}+{\frac {z^{2}}{a^{2}}}=1}$
paraboloida eliptyczna	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-z=0}$
paraboloida obrotowa     (szczególny przypadek paraboloidy eliptycznej)	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{a^{2}}}-z=0}$
paraboloida hiperboliczna	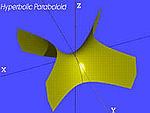${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}-z=0}$
hiperboloida jednopowłokowa	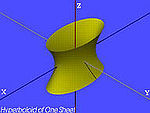${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=1}$
hiperboloida dwupowłokowa	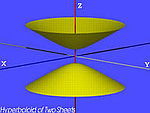${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=-1}$
powierzchnia stożkowa	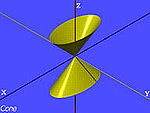${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=0}$
walec eliptyczny	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$
powierzchnia boczna zwykłego walca o nieskończonej wysokości     (szczególny przypadek walca eliptycznego)	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{a^{2}}}=1}$
walec hiperboliczny	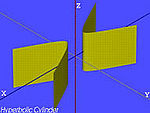${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$
walec paraboliczny	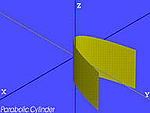${\displaystyle x^{2}+2ay=0}$
przecinające się płaszczyzny	${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=0}$
tzw. przecinające się płaszczyzny urojone	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=0}$	prosta
równoległe płaszczyzny	${\displaystyle x^{2}=a^{2}}$
nakładające się płaszczyzny	${\displaystyle x^{2}=0}$
tzw. równoległe płaszczyzny urojone	${\displaystyle x^{2}=-a^{2}}$	zbiór pusty
tzw. elipsoida urojona	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=-1}$	zbiór pusty
tzw. stożek urojony	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=0}$	pojedynczy punkt
tzw. urojony walec eliptyczny	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=-1}$	zbiór pusty

Ostatnie kilka przypadków opisuje kwadryki zdegenerowane, w których dla kanonicznego układu współrzędnych znika co najmniej jedna ze współrzędnych. Niektórzy autorzy nie zaliczają ich do kwadryk. W tym sensie także walce są przypadkami zdegenerowanymi, gdyż można je przedstawić w postaci zawierającej tylko dwie współrzędne. Ponadto warto zauważyć, że niektóre z tych zdegenerowanych kwadryk nie są powierzchniami (prosta, punkt, zbiór pusty).

Postać macierzowa równania

Równanie kwadryki można też przedstawić w postaci macierzowej:

${\displaystyle \mathbf {x} ^{T}\cdot \mathbf {A} \cdot \mathbf {x} +2\mathbf {a} ^{T}\cdot \mathbf {x} +a_{44}=0,}$

gdzie:

${\displaystyle \mathbf {A} ={\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{12}&a_{22}&a_{23}\\a_{13}&a_{23}&a_{33}\end{bmatrix}}}$

${\displaystyle \mathbf {a} ={\begin{bmatrix}a_{14}\\a_{24}\\a_{34}\end{bmatrix}}}$

${\displaystyle \mathbf {x} ={\begin{bmatrix}x\\y\\z\end{bmatrix}}}$

Niezmienniki

Poniższe wielkości nie zmieniają się przy zmianie początku układu współrzędnych i rotacji jego osi (równoważnie: przy przesuwaniu i obracaniu powierzchni względem układu współrzędnych):

${\displaystyle \Delta =\left|{\begin{matrix}a_{11}&a_{12}&a_{13}&a_{14}\\a_{12}&a_{22}&a_{23}&a_{24}\\a_{13}&a_{23}&a_{33}&a_{34}\\a_{14}&a_{24}&a_{34}&a_{44}\end{matrix}}\right|}$

${\displaystyle \delta =\det A=\left|{\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{12}&a_{22}&a_{23}\\a_{13}&a_{23}&a_{33}\end{matrix}}\right|}$

${\displaystyle S=a_{11}+a_{22}+a_{33}}$

${\displaystyle T=a_{22}a_{33}+a_{33}a_{11}+a_{11}a_{22}-a_{23}^{2}-a_{13}^{2}-a_{12}^{2}}$

Określenie typu na podstawie współczynników

Korzystając ze znaku niezmienników można określić typ powierzchni danej równaniem (1) niezależnie od jej położenia w układzie współrzędnych.

• ${\displaystyle \delta \neq 0}$ tzw. powierzchnie środkowe:
  • ${\displaystyle \Delta <0{:}}$
    • ${\displaystyle S\delta >0,\ T>0}$ elipsoida (w szczególnym przypadku sfera)
    • ${\displaystyle S\delta >0,\ T<0}$ hiperboloida dwupowłokowa
    • ${\displaystyle S\delta <0,\ T>0}$ hiperboloida dwupowłokowa
  • ${\displaystyle \Delta >0{:}}$
    • ${\displaystyle S\delta >0,\ T>0}$ zbiór pusty (tzw. elipsoida urojona)
    • ${\displaystyle S\delta >0,\ T<0}$ hiperboloida jednopowłokowa
    • ${\displaystyle S\delta <0,\ T>0}$ hiperboloida jednopowłokowa
  • ${\displaystyle \Delta =0{:}}$
    • ${\displaystyle S\delta >0,\ T>0}$ pojedynczy punkt (tzw. stożek urojony)
    • ${\displaystyle S\delta >0,\ T<0}$ powierzchnia stożkowa
    • ${\displaystyle S\delta <0,\ T>0}$ powierzchnia stożkowa
• ${\displaystyle \delta =0{:}}$
  • ${\displaystyle \Delta \neq 0}$ paraboloidy:
    • ${\displaystyle \Delta <0\Leftrightarrow T>0}$ paraboloida eliptyczna (w szczególnym przypadku paraboloida obrotowa)
    • ${\displaystyle \Delta >0\Leftrightarrow T<0}$ paraboloida hiperboliczna
  • ${\displaystyle \Delta =0{:}}$
    • ${\displaystyle \left|{\begin{matrix}a_{11}&a_{12}&a_{14}\\a_{12}&a_{22}&a_{24}\\a_{14}&a_{24}&a_{44}\end{matrix}}\right|+\left|{\begin{matrix}a_{11}&a_{13}&a_{14}\\a_{13}&a_{33}&a_{34}\\a_{14}&a_{34}&a_{44}\end{matrix}}\right|+\left|{\begin{matrix}a_{22}&a_{23}&a_{24}\\a_{23}&a_{33}&a_{34}\\a_{24}&a_{34}&a_{44}\end{matrix}}\right|=0}$
      przypadek zdegenerowany (suma dwóch płaszczyzn, jedna płaszczyzna, prosta lub zbiór pusty)
    • w przeciwnym wypadku powierzchnia walcowa oparta na krzywej stożkowej:
      • ${\displaystyle T>0}$ walec eliptyczny rzeczywisty lub urojony
      • ${\displaystyle T<0}$ walec hiperboliczny
      • ${\displaystyle T=0}$ walec paraboliczny

Przypisy

Bibliografia

• I.N. Bronsztejn, K.A. Siemiendiajew: Matematyka – Poradnik encyklopedyczny. Wyd. 6. Warszawa: Państwowe Wydawnictwo Naukowe, 1976, s. 299–301.

Linki zewnętrzne

• Interaktywne aplety Javy rysujące różne rodzaje kwadryk (ang.)