Liczba Poissona

Sześcian o krawędziach długości ${\displaystyle L}$ wykonany z izotropowego liniowo sprężystego materiału, o współczynniku Poissona równym 0,5, poddany obciążeniu w kierunku ${\displaystyle x.}$ Zielona kostka pokazuje stan początkowy, czerwona rozciągnięta pod wpływem przyrostu obciążenia na kierunku ${\displaystyle x}$-owym o długość ${\displaystyle \Delta L}$ oraz równocześnie skrócona na kierunku ${\displaystyle y}$ i ${\displaystyle z}$ o długość ${\displaystyle \Delta L'.}$

Współczynnik (liczba) Poissona ${\displaystyle (\nu )}$ – stosunek odkształcenia poprzecznego do odkształcenia podłużnego^[1] przy jednoosiowym stanie naprężenia.

Jednoosiowy stan naprężenia to stan reprezentowany tylko przez jedno niezerowe naprężenie główne.

Współczynnik Poissona jest wyrażony bezjednostkowo - znaczy to, że jest wielkością bezwymiarową, nie określa sprężystości materiału, a jedynie sposób, w jaki się on odkształca.

Jeżeli w przypadku materiału izotropowego w rozpatrywanym punkcie ciała wyróżnimy kierunek ${\displaystyle m}$ i jeżeli w tym punkcie jedynie naprężenie ${\displaystyle \sigma _{m}\neq 0}$ (zaś pozostałe składowe naprężenia są równe zero), to współczynnik Poissona:

${\displaystyle \nu =-{\frac {\varepsilon _{n}}{\varepsilon _{m}}},}$

gdzie:

${\displaystyle \varepsilon }$ – odkształcenie,

${\displaystyle n}$ – dowolny kierunek prostopadły do ${\displaystyle m.}$

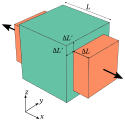
Jeżeli pręt o średnicy ${\displaystyle d}$ (lub dowolnym innym stałym przekroju) i długości ${\displaystyle L}$ zostanie poddany jednoosiowemu rozciąganiu tak, że wydłuży się o ${\displaystyle \Delta L,}$ to jego średnica zmieni się (zmniejszy się, stąd dla uniknięcia wartości ujemnych współczynnika znak minus we wzorze) o:

${\displaystyle \Delta d=-d\cdot \nu {\frac {\Delta L}{L}},}$

${\displaystyle \nu =-{\frac {\Delta d}{d}}{\frac {L}{\Delta L}}.}$

Wzór ten jest słuszny w przypadku małych odkształceń. Jeżeli odkształcenia są znaczne (patrz: duże odkształcenia), to dokładniejsze wyniki daje wzór (w założeniu ${\displaystyle \nu ={\text{const}}}$):

${\displaystyle \Delta d=-d\cdot \left(1-{\left(1+{\frac {\Delta L}{L}}\right)}^{-\nu }\right).}$

Powyższe wzory są jednym ze sposobów bezpośredniego wyznaczenia współczynnika Poissona w statycznej próbie rozciągania, chociaż ze względu na niewielkie odkształcenia jest to metoda niedokładna.

Ze względu na zależność opisującą stosunek współczynnika Poissona do modułu Younga i modułu Helmholtza można określić, że^[2][3]:

${\displaystyle -1\leqslant \nu \leqslant {\frac {1}{2}}.}$

W przypadku dwuwymiarowej sprężystości relacja ta przybiera postać:

${\displaystyle -1\leqslant \nu \leqslant 0{,}5.}$

Nazwa współczynnika pochodzi od nazwiska Siméon Denis Poissona (1781–1840), francuskiego matematyka.

Metodę określania współczynnika Poissona przedstawia norma ASTM E-132.

Współczynnik Poissona można również wyznaczyć, przekształcając równianie wiążące ten współczynnik z modułem Younga

${\displaystyle E=2G\cdot (\nu +1),}$

gdzie:

${\displaystyle E}$ – moduł Younga,

${\displaystyle G}$ – moduł Kirchhoffa,

${\displaystyle \nu }$ – Liczba Poissona.

Po przekształceniach uzyskujemy równanie:

${\displaystyle \nu ={\frac {E-2G}{2G}}.}$

Rozciąganie kostki z materiału o ujemnym współczynniku Poissona. Przykład auksetyku.

Zobacz też

• auksetyk
• moduł Kirchhoffa
• prawo Hooke’a
• stałe Lamégo

Przypisy