Liczenie na palcach
Liczenie na palcach – posługiwanie się palcami dłoni jako materiałem pomocniczym przy wykonywaniu prostych operacji arytmetycznych.
Zasady związane z liczeniem na palcach
Naukowcy Rochel Gelman oraz Charles Ransom Gallistel w 1986 roku opracowali pięć zasad, na których opiera się umiejętność liczenia na palcach[1][2]:
- stałość kolejności liczebników – np. po jeden zawsze jest dwa, a nie np. trzy[1][2]
- brak znaczenia kolejności obiektów[1][2];
- wszystkie obiekty mogą być liczone w ten sam sposób[1][2];
- wzajemnie jednoznaczna odpowiedniość[a] – każdej liczbie przypisana jest dokładnie jedna etykieta werbalna[1][2];
- liczebnik na ostatnim miejscu sekwencji liczenia oznacza liczność danego zbioru – np. gdy na głos po kolei policzymy swoje palce: pierwszy, drugi, trzeci, czwarty, piąty, szósty, siódmy, ósmy, dziewiąty, dziesiąty, to fakt iż ostatni policzony palec był dziesiąty, oznacza, że wszystkich palców jest dziesięć[1][2].
Posługiwanie się palcami okazuje się bardzo pomocne w zrozumieniu tych zasad, ponieważ w przeciwieństwie do liczebników palce są ciągle widoczne i dostępne, a także bardziej rozróżnialne percepcyjnie niż liczebniki (werbalne etykiety liczb), które muszą być zapamiętane[2].
Użyteczność palców
Przyczyny wysokiej użyteczności palców do liczenia na nich są następujące[3]:
- palce umożliwiają tworzenie wzrokowo-przestrzennej reprezentacji liczb[4], są łatwo rozróżnialne percepcyjnie i reprezentują kolejne dyskretne wartości[5];
- palce umożliwiają zrozumienie dziesiętnego systemu liczbowego[6];
- palce pomagają zrozumieć zasadę wzajemnej jednoznaczności[5][7];
- liczenie na palcach pozwala odciążyć pamięć roboczą podczas wykonywania operacji matematycznych oraz systematycznie kontrolować poprawność[5];
- w przeciwieństwie do cyfr arabskich lub zbiorów reprezentacje palców pozwalają zrozumieć istotę liczby kardynalnej (ostatni liczebnik wypowiedziany podczas liczenia określa łączną liczbę obiektów w zestawie)[4];
- palce umożliwiają realizację podstawowych operacji arytmetycznych na liczbach jednocyfrowych[8];
- za pomocą palców można liczyć od dowolnej liczby[6];
- palce pozwalają śledzić liczbę słów wypowiadanych podczas sekwencji liczenia[9];
- własne palce stanowią narzędzie, które każdy człowiek ma zawsze przy sobie[3][5];
- palce zazwyczaj nie są zakryte przez ubranie, więc łatwo na nich manipulować[5],
- palce mogą być wykorzystane zarówno do określenia liczby kardynalnej (liczebność zbioru), jak i porządkowej (kolejność obiektów)[5][10].
Szkodliwość zabraniania dzieciom liczenia na palcach
Dzieci na pewnym etapie rozwoju używają palców do liczenia i obliczania, nawet jeśli zostało to zabronione[11]. Bardzo szkodliwe jest zabranianie używania palców do liczenia dzieciom, które tego potrzebują[3][12][13]. Hamuje to rozwój matematyczny dziecka, uniemożliwia mu samodzielne zdobywanie i rozwijanie wiedzy matematycznej[3][12][13]. Ponadto, nawet gdy dziecko opanuje już liczenie w pamięci, w pewnych sytuacjach nadal może wspomagać się liczeniem na palcach[3][13].
Badania dowodzą, że do tworzenia abstrakcyjnych pojęć wykorzystywane są te same obwody neuronalne, które pierwotnie służyły do wykonywania operacji percepcyjnych i motorycznych[b][5].
Liczenie na palcach i nawyki z nim związane mają też wpływ na umysłowe przetwarzanie liczb i charakter ich reprezentacji nie tylko u dzieci, ale także u osób dorosłych[14][15]. Liczenie na palcach nie jest przejściowym etapem w rozwoju, a nawyki liczenia na palcach mają wpływ na przebieg wykonywanych w pamięci obliczeń arytmetycznych[15][16]. Umiejętności nabyte podczas liczenia na palcach mogą pozwolić uczniom w przyszłości tworzyć własne, skuteczne strategie rozwiązywania problemów matematycznych – przykładowo zadanie pewien uczeń rozwiązał następująco: biorę po 5 z szóstki i siódemki, więc zostanie mi 1 i 2, czyli 3, więc wynik to 13 – co stanowi strategię arytmetyczną odwołującą się do liczenia na palcach – rozbicie liczb na piątki, czyli na całe dłonie[15]. Uczeń nie stworzyłby takiej strategii, gdyby nie miał doświadczenia z liczeniem na palcach[15]. Liczenie na palcach na początku edukacji matematycznej dziecka zwiększa prawdopodobieństwo, że uzyskane przez niego wyniki działań arytmetycznych będą poprawne, zaś wielokrotne uzyskiwanie tych samych, poprawnych wyników, utrwala w jego umyśle prawidłowe fakty arytmetyczne[17][18]. Dotyczy to głównie prostego dodawania[17]. Przykładowo, jeśli uczeń przy dodawaniu wielokrotnie uzyska wynik 15, to z czasem utrwali i zapamięta, że i wykonywanie tego prostego działania nie będzie już wymagało ponownego przeliczania, a jedynie przywołania faktu arytmetycznego z pamięci długotrwałej[17][18]. Siła asocjacji zależy od wcześniejszych doświadczeń[18]. Będzie ona wysoka u dziecka, które wielokrotnie poprawnie wykonało to równanie, zaś dość niska u dziecka, które przy rozwiązywaniu tego równania wiele razy się myliło[18].
Bardzo szkodliwe jest także zabranianie liczenia na palcach dzieciom cierpiącym na dyskalkulię[19][20]. Stosowane przez te dzieci strategie liczenia na palcach są nieoptymalne i doprowadzają do licznych błędów, lecz po zabronieniu liczenia na palcach, dzieci te popełniają jeszcze więcej błędów[19][20].
Liczenie na palcach a osiągnięcia szkolne w zakresie matematyki
Liczenie na palcach pełni ważną funkcję w procesie nabywania kompetencji matematycznych przez dzieci oraz w poznaniu matematycznym u osób dorosłych[3]. W badaniach longitudinalnych (od początku przedszkola do końca drugiej klasy szkoły podstawowej) uzyskano wyniki świadczące o tym, że dzieci liczące na palcach lepiej sobie radzą z rozwiązywaniem problemów matematycznych, choć wraz z wiekiem wielkość korelacji maleje[3][21].
Liczenie na palcach a przechodzenie od reprezentacji konkretnych do abstrakcyjnych
Naturalną kolejnością rozwoju umiejętności liczenia jest przechodzenie od reprezentacji konkretnych do abstrakcyjnych[2]. Jako reprezentację abstrakcyjną rozumie się liczenie w pamięci[22]. Według prof. dr. hab. Edyty Gruszczyk-Kolczyńskiej i Ewy Zielińskiej, w pierwszej fazie rozwoju umiejętności liczenia dziecko powinno opanować umiejętności:
- zliczania obiektów,
- odróżniania prawidłowego liczenia od błędnego,
- dodawania,
- odejmowania[22].
Najpierw wykonywane jest to na materiale konkretnym (np. zabawki, klocki, liczmany)[22]. Później liczenie odbywa się na palcach[22]. Na końcu dziecko opanowuje umiejętność liczenia w pamięci[22]. Największe znaczenie ma jednak proces przejścia od materiałów konkretnych do własnych palców[22]. Posługiwanie się palcami jest czymś więcej niż wykorzystywaniem zewnętrznych obiektów[23]. Jest to w pewnym stopniu oderwanie od konkretów (palce stają się reprezentantami innych obiektów)[22]. W toku edukacji nauczyciel powinien pokazać dziecku, że zamiast przedmiotów konkretnych do liczenia można wykorzystać własne palce[22].
Według profesora Wygotskiego rozwój umiejętności arytmetycznych dziecka można podzielić na 4 etapy[24]:
- Stadium naturalnych reakcji arytmetycznych – jest to percepcja ilości, ogólna percepcja liczebności, porównywanie mniejszych i większych zbiorów przedmiotów itp.[24];
- Stadium naiwnej psychologii – dziecko próbuje naśladować liczenie dorosłych, lecz nie ma świadomości, w jaki sposób należy liczyć korzystając z cyfr[24] (przykładem zachowania dziecka w tym stadium jest sytuacja, w której dziecko poproszone o policzenie palców innej osoby odpowiada, że potrafi policzyć wyłącznie własne palce[24]);
- Stadium liczenia na palcach – dziecko opanowało umiejętność liczenia na palcach[24];
- Stadium liczenia w pamięci – dziecko potrafi już liczyć w pamięci, w większości sytuacji nie musząc wspomagać się palcami[24].
Przystępność palców a przystępność liczebników
Istnieje hipoteza postawiona przez Heike Wiese w 2003 roku, mówiąca o tym, że pokazywane na palcach liczby są dla dzieci w wieku przedszkolnym bardziej przystępne niż liczebniki[25]. Zdania naukowców na temat tej hipotezy są podzielone[15].
Istnieją badania potwierdzające, że palce są wykorzystywane w ontogenezie, zanim wykształci się reprezentacja symboliczna (np. cyfry lub liczebniki)[26].
Istnieją także badania stwierdzające coś przeciwnego – że symboliczne systemy liczenia nie są zakorzenione w doświadczeniach cielesnych[27]. Badaniu poddano dzieci w wieku 2–5 lat[27]. Podzielono je na dwie grupy – pierwsza składała się z dzieci 2–3-letnich, a druga – z 4–5-latków[27]. Badacze poprosili dzieci o umieszczenie w pudełku liczby zabawek, którą przekazali dzieciom poprzez podanie liczebnika lub poprzez pokazanie liczby na palcach[27]. W grupie dzieci 2–3-letnich w obu przypadkach dzieci miały duże problemy z wykonaniem zadania[27]. W grupie dzieci starszych okazało się, że dzieci lepiej radziły sobie z wykonaniem polecenia, gdy liczba została im podana w formie liczebnika[27]. Gdy dzieci proszono o określenie liczby zabawek w pudełku, ponownie okazało się, że dzieciom łatwiej jest posługiwać się liczebnikami, niż palcami[27].
Okazuje się, że liczenie na palcach nie może zastąpić kodu werbalnego[28]. Jeśli nie istnieje odpowiedni kod werbalny (np. nazwy liczebników), nie jest możliwe efektywne liczenie na palcach[28]. Np. w amazońskim plemieniu Pirahã istnieją tylko nazwy: jeden, dwa i wiele[28]. Przedstawiciele tego plemienia wspomagają się liczeniem na palcach, lecz nawet wtedy popełniają mnóstwo błędów rachunkowych, nawet w przypadku zbiorów mniejszych niż 5-elementowe[28].
Podobnie osoby głuchonieme, które wykształtowały swój własny język migowy, liczą na palcach w sposób bardzo niedokładny[28].
Kolejność używania palców a kolejność liczb
Istnieją sprzeczne wyniki badań na temat związku kolejności używania palców a kolejności liczb[2]. W jednych publikacjach (np. H. Wiese) za korzystne uważa się używanie palców zawsze w tej samej kolejności. Według tych poglądów utrwala to wiedzę na temat kolejności liczb[25]. W innych pracach (np. prof. dr. hab. Zbigniewa Semadeniego) zwraca się uwagę na korzyści płynące z kształcenia umiejętności liczenia na palcach w różnej kolejności – np. reprezentacją liczby dwa wcale nie muszą być zawsze wyciągnięty kciuk i palec wskazujący, może to być np. palec wskazujący i serdeczny, lub dowolna inna kombinacja dwóch palców[12]. Semadeni uważa, że narzucanie sposobu liczenia na palcach w ustalonej kolejności utrudnia przechodzenie do poziomu operacyjnego według teorii Piageta[12].
Liczenie na palcach a pamięć robocza
Podczas wykonywania obliczeń matematycznych kluczowe jest poprawne działanie pamięci roboczej[29]. Jej zadaniem jest:
- przechowywanie liczb, na których wykonywane są działania,
- przywoływanie z pamięci długotrwałej, reguł wykonywania działań (np. kolejność wykonywania działań),
- przechowywanie wyników cząstkowych[c][29].
U dzieci często zdarza się, że ilość informacji, którą muszą przechować w pamięci roboczej w celu rozwiązania zadania, przekracza pojemność i czas przechowywania w tej strukturze pamięciowej[29]. Dzieci dysponujące niewielką pojemnością pamięci roboczej mogą stosować strategie jej odciążania, np. zapisywanie wyników cząstkowych na papierze lub wręcz monotonne przeliczanie wszystkiego po kolei na palcach[29][30].
Okazuje się, że na zakres pamięci roboczej ma wpływ długość liczebników – u dzieci posługujących się językiem chińskim (liczebniki w tym języku są znacznie krótsze niż w języku angielskim) zakres pamięci roboczej jest większy, a dzieci te podczas liczenia mniej wspomagają się palcami[31][29].
Split 5 errors
Podczas wykonywania operacji arytmetycznych przekraczających liczbę 10 dzieci bardzo często mylą się dokładnie o 5[15][16]. Ma to nawet w literaturze specjalistycznej swoją nazwę: split 5 errors[16][15]. Przykładowo – dla zadania częstymi odpowiedziami będą: 12, 17, 22, a split 5 errors będą jeszcze wyraźniej widoczne dla większych liczb, np. [16].
Istnieją dwa źródła tego błędu:
- W przypadku gdy split 5 error wystąpi podczas rozwiązywania łatwego problemu, jego źródłem jest błąd w przywoływaniu wyników z pamięci długotrwałej[15][16];
- W przypadku gdy split 5 error wystąpi podczas rozwiązywania złożonego problemu, jego źródłem jest błąd w monitorowaniu liczby „pełnych dłoni” (uczeń gubi się już w tym ile już „ma” całych piątek, pełnych dłoni)[16][15].
Dzieci same próbują eliminować split 5 errors, tworząc własne, różnorodne strategie, jak np. dotykanie lub zamykanie jednej dłoni[32][15].
Choroby a liczenie na palcach
Dyskalkulia
Osoby cierpiące na dyskalkulię mają znaczne deficyty w zakresie elementarnych procesów umysłowego przetwarzania liczb[29]. Dyskalkulicy popełniają ogromne ilości błędów podczas liczenia na palcach[29]. Mają duże problemy z opanowaniem metody liczenia na palcach, a gdy już ją opanują – stosują ją w bardzo nieoptymalny sposób[29]. Mając dodać do siebie dwie duże liczby, np. nie potrafią zastosować strategii dodawania osobno dziesiątek i jedności[29]. Dzieci cierpiące na dyskalkulię do liczby 35 będą na palcach dodawać po kolei 23 jedności, co jest strategią bardzo czasochłonną i narażoną na liczne pomyłki, więc sam wynik często również będzie nieprawidłowy[29]. Wraz z dyskalkulią może występować także dyspraksja i agnozja palców, co bardzo utrudnia wykorzystywanie palców do liczenia[29]. Często jednak liczenie na palcach jest najlepszą dostępną dla tych dzieci strategią, umożliwiającą względnie poprawne wykonywanie obliczeń[29]. Zabronienie liczenia na palcach osobom z dyskalkulią powoduje, że popełniają one jeszcze więcej błędów[19].
Rozwojowy zespół Gerstmanna
Zespół Gerstmanna to zaburzenie towarzyszące lezjom w obszarze zakrętu kątowego półkuli dominującej, składające się z czterech podstawowych objawów:
Rozwojowy zespół Gerstmanna ma te same objawy, lecz jego źródłem nie są lezje i nie dotyczy on wyłącznie półkuli dominującej[34]. W zaburzeniu tym występują deficyty zarówno w zakresie gnozji palców, jak i w zakresie liczenia, co przez naukowców jest interpretowane jako dowód na nierozłączny związek między liczeniem na palcach, a liczeniem w ogóle[34].
Zespół Gerstmanna sprawił, że już w pierwszej połowie XX wieku po raz pierwszy został dostrzeżony związek między gnozją palców, a ogólnymi zdolnościami liczenia[20].
Liczenie na palcach u dzieci niewidomych lub niemających palców
Istnieją sprzeczne wnioski na temat tego, czy liczenie na palcach jest czynnością spontaniczną, czy ukształtowania drogą modelowania[2]. Np. Butterworth w swojej publikacji stwierdza, że liczenie na palcach jest czynnością spontaniczną, powszechną w większości kultur[11]. Spontaniczność liczenia na palcach potwierdza także przypadek dziewczynki urodzonej bez przedramion, wykorzystującej do liczenia swoje fantomowe palce, co zostało opisane w 1965 roku[35][3]. Teorii o spontaniczności liczenia na palcach zaprzeczają badania na dzieciach niewidomych[3]. W jednym z badań porównano dzieci widzące z niewidomymi – dzieci niewidzące stosowały liczenie na palcach o wiele rzadziej niż widzące[36]. Mimo tego, dzieci w obu grupach osiągały podobną poprawność obliczeń[36]. Dzieci niewidzące miały niższe wyniki tylko wtedy, gdy zadania silnie angażowały zasoby werbalnej pamięci roboczej[36]. Zatem nie u wszystkich dzieci liczenie na palcach pojawia się spontanicznie oraz nie jest ono warunkiem koniecznym rozwoju umiejętności matematycznych[3].
Osoby niewidome, korzystając z liczenia na palcach, nie korzystają z powtarzalnych układów palców (tzn. te same liczby w różnych przypadkach reprezentują innymi układami palców)[36].
Gnozja palców a kompetencje matematyczne
Gnozja palców to zdolność do określania, który palec jest w danym momencie stymulowany, umiejętność nazywania palców oraz sprawnego posługiwania się nimi[34]. Sprawność gnozji palców koreluje z poziomem osiągnięć matematycznych[34][37][38][39][40][41]. W licznych badaniach na dzieciach w wieku 5–7 lat wykazano, że dzieci osiągające ponadprzeciętne wyniki w zakresie gnozji palców mają również wysokie umiejętności matematyczne, a gnozja palców jest jednym z najlepszych znanych predyktorów osiągnięć z matematyki, w perspektywie czasowej od 1 do 3 lat[34][37][38][39][40][41]. Moc predykcyjna testów gnozji palców jest specyficzna dla osiągnięć matematycznych – testy te nie pozwalają przewidywać osiągnięć w zakresie czytania i pisania[34][37][38][39][40][41]. Gnozja palców jest lepszym predyktorem zdolności matematycznych niż gnozja całego ciała, symultagnozja lub grafestezja[34][39]. Gnozja palców ma również większą moc predykcyjną dla późniejszych osiągnięć matematycznych niż ogólne wskaźniki rozwoju, takie jak np. szybkość przetwarzania informacji[34][39].
Wykazano również, że dzieci sprawnie posługujące się palcami (np. z racji gry na pianinie czy gitarze) lepiej radzą sobie z rozwiązywaniem zadań matematycznych[30][42]. W roku 2008 opublikowano również wyniki eksperymentu, w którym grupę dzieci z niskimi wynikami gnozji palców, poddano intensywnemu treningowi tej gnozji[30][42]. W rezultacie zwiększyły swoje zdolności gnozji palców, subityzowania oraz w niewielkim stopniu także umiejętności matematyczne[30][34]. Trening w zakresie gnozji palców musi być bardzo intensywny, aby przełożył się na umiejętności matematyczne[30][42].
Gnozję palców bada się zazwyczaj w następujący sposób:
- dłoń osoby badanej znajduje się poza zasięgiem jej wzroku, a badacz dotyka wybranego palca osoby badanej; jej zadaniem jest określenie, który palec został dotknięty[34];
- dłoń osoby badanej znajduje się poza zasięgiem jej wzroku, a badacz dotyka po kolei dwa wybrane przez siebie palce osoby badanej; jej zadaniem jest określenie, czy dwukrotnie został dotknięty ten sam palec, czy dwa różne palce[34].
Istnieją dwie główne teorie próbujące wyjaśniać wzajemne powiązanie między gnozją palców a umiejętnościami matematycznymi[20]:
- Teoria funkcjonalistyczna: wedle tej teorii gnozja palców jest pierwotna wobec poznania matematycznego[20]
- Hipoteza przesunięcia funkcji neuronów: neurony przystosowane ewolucyjnie do liczenia na palcach mogą na skutek egzaptacji przyjąć nowe role (abstrakcyjne poznanie matematyczne), zachowując jednocześnie pierwotne funkcje (liczenie na placach)[20];
- Hipoteza recyklingu neuronów: obwody neuronalne wykształcone do zdolności subityzowania na skutek rozwoju kulturowego gatunku ludzkiego zaczęły być wykorzystywane do arytmetyki[20];
- Teoria lokalizacjonistyczna: wedle tej teorii za gnozję palców i za poznanie matematyczne odpowiadają inne obwody neuronalne, lecz są zlokalizowane tak blisko siebie, że są zasilane przez te same naczynia krwionośne[20].
Związek między gnozją palców i liczeniem w pamięci potwierdzają także badania doświadczalne[43]. Przebadano osoby dorosłe o przeciętnych umiejętnościach matematycznych, nie mające żadnych dysfunkcji[43]. Okazało się, że wykonywanie przez te osoby działań arytmetycznych związanych z liczeniem (a nie przywoływaniem wyników z pamięci) było mniej skuteczne, gdy eksperymentator poruszał w tym czasie palcami osób badanych[43].
Co więcej, odkryto także, że w czasie biernego obserwowania liczb jednocyfrowych rośnie aktywacja kory motorycznej, odpowiedzialnej za ruchy palców podczas liczenia na palcach[43][44]. Zaobserwowany efekt zależny był od indywidualnych zwyczajów liczenia na palcach[43][44]. U osób zaczynających liczenie od lewej ręki podczas prezentacji małych liczb rosła aktywacja prawej kory motorycznej, zaś u osób zaczynających od prawej ręki – aktywacja lewej kory motorycznej[43][44]. Wykazano także zmiany pobudliwości korowej dla mięśni dłoni podczas liczenia – ponownie strona, po której obserwowano zwiększoną pobudliwość, zależna była od wielkości liczb wykorzystywanych w działaniach oraz od strony, po której osoby badane zwyczajowo zaczynały liczenie na palcach[45].
Przedmotoryczna teoria liczenia
Przedmotoryczna teoria liczenia to potwierdzona doświadczalnie teoria stwierdzająca, że wykonywanie działań arytmetycznych w pamięci polega na symulowanych, choć niewykonywanych fizycznie ruchach palców dłoni, o czym świadczy pobudzenie kory motorycznej podczas liczenia[45]. Efekt ten występuje zarówno u dzieci, jak i u dorosłych[45].
Strategie dodawania na palcach
Można wyróżnić trzy podstawowe strategie używania palców do obliczania sumy dwóch liczb naturalnych[46]:
- count-all: strategia ta polega na przedstawieniu każdej z liczb przy pomocy prostowania palców, a następnie zliczenie wszystkich wyprostowanych palców[46]. Przykładowo, mając dodać 2 do 3, na jednej dłoni uczeń prostuje dwa palce, a na drugiej – 3, a następnie zlicza po kolei wyprostowane palce, co daje w wyniku liczbę 5[46].
- count-from-first-addend: strategia ta polega na rozpoczęciu liczenia od pierwszego składnika sumy, a następnie wymieniania odpowiedniej liczby kolejnych liczb (prostując przy tym palce)[46]. Przykładowo, mając wykonać działanie uczeń policzy: trzy, cztery, pięć, sześć, siedem[46].
- count-min: strategia ta opiera się na tej samej zasadzie, co count-from-first-addend, z tą różnicą, że dodatkowo znajdowany jest składnik większy w sumie i to od niego rozpoczyna się liczenie[17]. Przykładowo, mając wykonać działanie uczeń zauważa, że 4 jest większe od 3 i liczy: cztery, pięć, sześć, siedem[17].
Dzieci, wraz z wiekiem, samodzielnie odkrywają i automatycznie zaczynają stosować strategię count-min, która jest strategią optymalną[17]. Nie da się określić jednoznacznie wieku, w którym dzieci rozpoczynają stosowanie tej strategii, ponieważ badania pokazują duże rozbieżności wieku[17]. Często zdarza się również że strategia ta jest używana równolegle z innymi, mniej skutecznymi strategiami[17].
Liczenie na palcach w historii dydaktyki matematyki
Zjawisko liczenia na palcach przez długi czas nie spotykało się z zainteresowaniem dydaktyków matematyki[47]. Do lat 70. XX wieku uważano, że mentalna arytmetyka jest oparta wyłącznie na abstrakcyjnych, symbolicznych manipulacjach[47]. Liczenie na palcach było uznawane jedynie za przejściowy etap w rozwoju kompetencji matematycznych dzieci[42]. Dopiero wyniki badań z ostatnich 20 lat wskazują na ogromne znaczenie liczenia na palcach dla poznania matematycznego u dzieci i u dorosłych[2]. Badania te prezentują różnorodną metodologię, jak np. [2]:
- przezczaszkowa stymulacja magnetyczna[26],
- neuroobrazowanie[48][49][50],
- neuropsychologia poznawcza[39][40].
W roku 2011 zagadnieniu liczenia na palcach poświęcono cały specjalny numer czasopisma naukowego „Frontiers in Psychology”[5].
Anatomiczne pochodzenie liczebników
Istnieje hipoteza o anatomicznym pochodzeniu liczebników[51]. Istnieje wiele dowodów ją potwierdzających[52]. Tworzenie się liczb rozpoczęło się liczeniem na palcach, a wraz z rozwojem ludzkości temu procesowi zaczęły towarzyszyć wypowiadane nazwy, które później funkcjonowały już niezależnie[25][52]. Liczenie na palcach pojawiało się w filogenezie gatunku ludzkiego bardzo wcześnie[52]. Pierwsze dowody tego zjawiska pochodzą sprzed 27 tysięcy lat – w jaskini Cosquer (Francja) maczane w pigmencie palce ówcześni ludzie odciskali na ścianie[52]. Układy te były bardzo regularne, zawsze rozpoczynały się od kciuka[52].
U wielu pierwotnych plemion wyróżnionymi liczebnikami bardzo często są liczby 2 i 5 (dwie ręce, pięć palców u ręki)[51]. W niektórych systemach liczebników zdarza się także wyróżnienie liczby 10 i 20 (łączna liczba palców u rąk, łączna liczba palców u wszystkich kończyn)[51]. Zatem pochodną systemu liczbowego z bazą 5 jest system dziesiętny, ale też dwudziestkowy system liczbowy. W nahuatl, języku Azteków, wyróżnione liczby to 5 (6 jest konstruowane jako „pięć-jeden”), 10 (11 to „dziesięć-jeden”), 15, 20 (30 to „jedna dwudziestka-dziesięć”, 40 to „dwie dwudziestki”, a 100 to „pięć dwudziestek”) i 400[53]. Ślady wyróżniania 20 występowały też w języku angielskim, gdzie liczbę tę określano jako score, a niektóre liczby były wyrażane jako jej wielokrotności (40 – two scores, 240 – twelve scores)[54].
| 1 | ke-yap |
| 2 | pullet |
| 3 | ke-yap-pullet |
| 4 | pullet-pullet |
| 1 | enea |
| 2 | patcheval |
| 3 | patcheval enea |
| 4 | patcheval patcheval |
| 1 | tagogi | |
| 2 | ruag’a | |
| 3 | tonug’a | |
| 4 | ruag’a-ma-ruag’a | 2 + 2 |
| 5 | ura-i-ga | |
| 6 | ura-g’ela-tagogi | 5 i 1 |
| 7 | ura-g’ela-ruag’a | 5 i 2 |
| 8 | ura-g’ela-tonug’a | 5 i 3 |
| 9 | ura-g’ela-ruag’a-ma-ruag’a | 5 i 2 + 2 |
| 10 | ura-ruag’a-i-ga | 5 × 2 |
| liczba | wyspy Hense-Vulkan (wyróżnione liczby 5 i 10)[51] | język api (Nowe Hebrydy)[55] |
| 1 | teé | tai |
| 2 | rua | lua |
| 3 | tolli | tolu |
| 4 | oatti | vari |
| 5 | lima | luna (‘ręka’) |
| 6 | lima teé | otai ('nowe 1') |
| 7 | lima rua | olua ('nowe 2') |
| 8 | lima tolli | otolu ('nowe 3') |
| 9 | lima oatti | ovari ('nowe 4') |
| 10 | ulema | lualuna (‘dwie ręce’) |
| 11 | ulema teé | lualuna i tai |
| ... | ... | |
| 15 | ulema lima | tololuna |
| 16 | ulema lima teé | tololuna i tai |
| ... | ... | |
| 20 | ulem tamata | variluna |
| 1 | sznepf | |
| 2 | tup | |
| 3 | repf | |
| ... | ... | |
| 8 | tubiszambi | 8=10-2 |
| 9 | sznebiszambi | 9=10-1 |
| 10 | vambi |
| 18 | duo de viginti | 18=20-2 |
| 19 | un de viginti | 19=20-1 |
Sztandarowym przykładem potwierdzającym hipotezę anatomicznego pochodzenia liczebników są nazwy liczebników u Tamanków (Indianie z Wenezueli)[51].
| 1 | tevinitpe | |
| 2 | akčake | |
| 3 | ačiluove | |
| 4 | akčakemnene | „powtórzone dwa” |
| 5 | amgnaitone | „cała ręka” |
| ... | ... | |
| 10 | amgna-ačeponare | „obie ręce” |
| 11 | puitta-pona tevinitpe | „jeden u nogi” |
| ... | ... | |
| 15 | iptaitone | „cała noga” |
| 16 | itakono puitta-pona tevinitpe | „jeden u drugiej nogi” |
| ... | ... | |
| 20 | tevin itoto | „jeden Indianin” |
| 21 | itakono itoto jamgnar-pona tevinitpe | „jeden u ręki drugiego Indianina” |
| ... | ... | |
| 40 | akčake itoto | „dwóch Indian” |
| ... | ... | |
| 60 | ačiluove itoto | „trzech Indian” |
Również w kilku innych językach nazwy wyraźnie oznaczają pewne czynności związane z liczeniem na palcach[52]. Przykładowo, w indiańskim języku dene-dinje, nazwy liczb od 1 do 5 pochodzą bezpośrednio od reprezentujących je układów palców (np. liczebnik odpowiadający liczbie 4 oznacza dosłownie końcowy jest zgięty)[52]. W nigero-kongijskim języku ali liczebnik 5 brzmi moro (‘ręka’), a 2 buna, natomiast 10 jest ich połączeniem: mbuna[56]. W papuaskim języku bugilai liczebniki mają pochodzenie anatomiczne: 1 tarangesa ('mały palec lewej ręki’), 2 metakina (‘następny palec’), 3 gingimetakina (‘palec środkowy’), 4 topea (‘palec wskazujący’), 5 manda (‘kciuk’)[56][57], 6 gaben (‘nadgarstek’), 7 trankgimbe (‘łokieć’), 8 podei (‘ramię’), 9 ngama (‘lewa pierś’), 10 dala (‘prawa pierś’)[57].
Ślady liczenia na palcach dłoni i stóp widać do dziś w bardzo wielu językach europejskich[d], poprzez wyróżnienie w nich liczby 20[51], np:
| Baskowie[51] | Bretończycy[51] | |||
|---|---|---|---|---|
| 10 | amar | |||
| 20 | oguey | 20 | ugent | |
| 30 | ogueyt-amar | 30 | tregont | |
| 40 | barroguey | 40 | daou ugent | 2 × 20 |
| 60 | yruroguey | 60 | tri ugent | 3 × 20 |
| 50 | half-tre-sinds-tyve | „półtrzecia × 20" |
| 60 | tre-sinds-tyve | „3 × 20" |
| 70 | half-fjerd-sinds-tyve | „półczwarta × 20" |
| 80 | fir-sinds-tyve | „4 × 20" |
| 80 | quatre-vingt[e] | 4 × 20 |
| 96 | quatre-vingt-seize | 4 × 20 + 16 |
W bardzo wielu językach również słowo określające liczbę pięć wywodzi się od słowa pięść[52]. Według niektórych badaczy również powszechnie stosowany dziesiątkowy system pozycyjny wywodzi się od tradycji liczenia na palcach (10 to liczba palców u obu rąk)[52]. Fuzja systemu piątkowego, ewentualnie dziesiętnego, z dwunastkowym mogła z kolei zaowocować popularnym w kulturach Mezopotamii systemem z bazą 60[58].
Georges Ifrah stawia hipotezę, że nawet system dwunastkowy, stosunkowo popularny, z tuzinem jako bazą, również może mieć podłoże anatomiczne, gdyż cztery palce jednej dłoni przeciwstawne kciukowi mają dwanaście członów i do dwunastu można liczyć używając jedynie końcówki kciuka dotykającej ich po kolei[59].
Liczenie na palcach przez osoby dorosłe
Nie tylko dzieci, ale również osoby dorosłe w wielu przypadkach korzystają z liczenia na palcach[60]. Odciążają w ten sposób pamięć roboczą oraz kontrolują poprawność, np. podczas wymieniania członków dalszej rodziny, albo wykonywania obliczeń na kalendarzu[60].
Różnice międzykulturowe
Kolejność liczenia na palcach
W większości krajów zachodnich (jak np. USA, Kanada, Wielka Brytania, Niemcy, Holandia, Hiszpania) średnio ok. 68% osób rozpoczyna liczenie od kciuka lewej ręki, np. w Szkocji jest to 66%[61]. Natomiast we Włoszech i Belgii nie wykazano preferencji żadnej ręki[61]. W krajach Bliskiego Wschodu istnieje preferencja prawej ręki – 64% badanych rozpoczynało liczenie od małego palca prawej ręki[61]. W północnej Afryce liczenie rozpoczyna się od palca wskazującego[59].
Natomiast we wszystkich krajach zauważono, że większość badanych podczas liczenia stosuje kontynuację anatomiczną, a nie przestrzenną – tzn. jeśli dla badanego liczba 1 to kciuk lewej ręki, to liczba 6 to kciuk prawej ręki, a nie mały palec prawej ręki (co byłoby zgodne z kolejnością przestrzenną)[61].
Sposób liczenia na palcach
W zdecydowanej większości kultur liczy się na palcach w ten sposób, że po kolei prostuje się kolejne palce[62]. Ale np. w Japonii robi się to na odwrót – zaczyna się od otwartej dłoni, a następnie zgina po kolei kolejne palce[62]. Sposoby liczenia na palcach w różnych kulturach przedstawione są na ilustracjach poniżej.
Liczenie a pokazywanie liczb
W większości kultur istnieje różnica między liczeniem na palcach, a pokazywaniem liczb na palcach[62]. Gdy osoby miały policzyć ile dni zostało im do końca urlopu, zaczynały liczyć od kciuka[62]. Gdy miały w głośnym barze zamówić np. dwa piwa, zaczynały od palca wskazującego[62]. Wyjątek stanowili Niemcy, ponieważ w obu przypadkach zaczynali od kciuka[62].
Liczenie powyżej 10
Palców obu rąk wystarcza do policzenia do dziesięciu[64]. Jedną z technik zwiększenia tej liczby jest nadanie różnych wartości palcom różnych dłoni[64]. Do pięciu liczy się wyciągając kolejne palce lewej ręki[64]. Wtedy zagina się palec prawej ręki i zaczyna liczenie od sześciu na lewej ręce[64]. Po dojściu do dziesięciu zagina się kolejny palec prawej ręki[64]. To pozwala na liczenie do 25[64]. Technikę tę stosowano w różnych regionach Afryki, Indii czy Oceanii[64]. Jeżeli za podstawę przyjmie się nie liczenie palców, ale ich członów, łatwo jest doliczyć do 12 na jednej dłoni (kciuk dotyka kolejnych członów czterech pozostałych palców)[65]. Zaginanie palców drugiej ręki po dojściu do końca bazy daje iloczyn 5·12, a więc pozwala liczyć do 60. System ten spotykany bywał w różnych regionach południowej Azji[65]. Gdy liczyć człony u palców obu rąk, można dojść do 28. Gdy zaś kość I śródręcza potraktować jak nasadowy człon kciuka, do 30[66]. W Chinach opracowano bardziej skomplikowany system podziału palców do liczenia[67]. Ponumerowano nie tylko człony palców, ale dodatkowo podzielono je na części lewą, prawą i środkową[67]. W ten sposób jeden palec może obsługiwać liczby 1-9, drugi 10-90 i tak dalej, aż do kciuka, na którym liczy się dziesiątki tysięcy, a przechodząc na kolejną rękę można liczyć miliardy[67].
Liczenie na palcach i ich członach w historii
Do początku XX wieku w krajach Orientu – od Maghrebu po Mongolię – podczas targowania się kontrahenci, chcąc ukryć przed obserwatorami negocjowaną cenę, przykrywali dłonie chustką i ściskali nawzajem palce[68]. Ściśnięcie palca wskazującego oznaczało 1, ściśnięcie naraz palca wskazującego i środkowego oznaczało 2 i tak dalej do całej dłoni, czyli 5[68]. Wyższe liczby tworzyła kombinacja, np. 6 to dwukrotne ściśnięcie palców wskazującego, środkowego i serdecznego (2·3), a 7 to ściśnięcie ręki bez kciuka (4) i następnie palców wskazującego, środkowego i serdecznego (3)[68]. Wymagało to założenia szacunkowej wartości towaru, aby uścisk mógł oznaczać 1, 10, 100 itd.[68] Liczenie do 28 na członach palców było stosowane w Chinach do wyznaczania cyklu miesiączkowego lub odchyleń od niego, a przez Bedę Czcigodnego do wyznaczania cyklu 28 lat związanych z określaniem lat przestępnych[69]. Ten sam mnich obliczał 19-letni cykl Metona przez dodanie liczby członów palców i paznokci jednej dłoni (14 + 5)[69]. Kombinacja tych cykli pozwalała tworzyć tablice paschalne[69]. Liczenie do trzydziestu na stawach palców i pierwszej kości śródręcza, a potem dodanie trzech bywa wykorzystywane przez muzułmanów w razie braku 33-paciorkowego islamskiego różańca[70].
W krajach Europy i Bliskiego Wschodu funkcjonował system liczenia na palcach, w którym jednostki wyraża się przez zginanie palców małego, serdecznego i środkowego, dziesiątki – wskazującego i kciuka, setki – małego, serdecznego i środkowego na drugiej ręce i tysiące – wskazującego i kciuka drugiej ręki[71]. W ten sposób można liczyć do 99 na palcach jednej ręki i 9 999 dwóch rąk[71]. System ten znany był w Starożytnym Rzymie, a pewne podobieństwa można znaleźć w jeszcze starszych malowidłach staroegipskich[71]. Następnie przejęła go średniowieczna arytmetyka zachodnia i islamska[71]. Znajomość tego systemu była elementem wykształcenia, a nawiązania do układu palców i odpowiadających im liczb pojawiały się w ówczesnej literaturze[71]. Stracił na popularności po upowszechnieniu się znajomości cyfr arabskich i rachunku przy ich użyciu[71].
Algorytmy mnożenia na palcach
Mnożenie liczby jednocyfrowej przez dziewięć
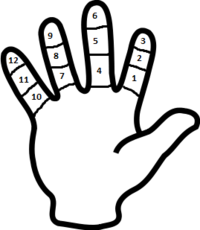
- Algorytm
Numerujemy swoje palce po kolei od lewego kciuka do prawego kciuka, nadając im kolejne numery od 1 do 10[72]. Chcąc pomnożyć liczbę przez dowolną liczbę ze zbioru wystarczy zgiąć palec o numerze [72]. Liczba palców znajdujących się na lewo od zgiętego palca to liczba dziesiątek, a liczba palców znajdujących się na prawo od zgiętego palca, to liczba jedności[72].
- Przykłady
- Dowód poprawności algorytmu
Niech będzie ustaloną liczbą[72]. Zauważmy, że:
co odpowiada właśnie podanej metodzie liczenia na palcach[72]. q.e.d.
Mnożenie dwóch liczb ze zbioru
- Algorytm
Metoda ta zakłada znajomość tabliczki mnożenia w zakresie od 0 do 4[72]. W obu dłoniach numerujemy palce zaczynając od kciuka, nadając mu numer 6, a kolejnym palcom – kolejne numery[72]. Wybieramy teraz dwie liczby, które będziemy chcieli przez siebie przemnożyć: [72]. Lokalizujemy na lewej dłoni palec o numerze i na prawej dłoni – palec o numerze i prostujemy te palce oraz wszystkie palce leżące na zewnątrz od nich[72]. Sumujemy liczbę wyprostowanych palców i mnożymy przez 10[72]. Następnie mnożymy liczbę zgiętych palców w lewej ręce, przez liczbę zgiętych palców w prawej ręce[72]. Otrzymaną liczbę dodajemy do wcześniej otrzymanego wyniku[72].
- Przykłady
- Dowód poprawności algorytmu
Niech będą ustalonymi liczbami, których iloczyn chcemy obliczyć[72]. Wynik osiągany w podanym algorytmie to:
- [72].
Zauważmy, że[72]:
q.e.d.
Uwagi
- ↑ Ta umiejętność bardzo często jest zaburzona u dzieci cierpiących na dyskalkulię.
- ↑ W uproszczony sposób można to rozumieć tak, że podczas obliczania czegoś w pamięci, aktywne są te same obszary mózgu, które aktywizują się przy liczeniu na palcach – dlatego ważne jest, by umożliwiać dzieciom liczenie na palcach, gdyż rozwija to u nich te obszary mózgu, które będą kluczowe dla liczenia w pamięci w późniejszym etapie rozwoju.
- ↑ Przykładowo: wykonując działanie najpierw mogę policzyć dziesiątki: a potem jedności: Jednak podanie ostatecznego wyniku wymaga przywołania z pamięci faktu, że pełnych dziesiątek mam już 6, co niejednokrotnie przekracza możliwości uczniów o niewielkiej pojemności pamięci roboczej lub dzieci z zaburzeniami w kierunku dyskalkulii, więc mimo poprawnego obliczenia wyników cząstkowych, nie są w stanie podać wyniku ostatecznego:
- ↑ Takich przykładów nie można znaleźć w języku polskim. Nazwy liczebników w języku polskim ukształtowały się dużo później, niż w większości krajów europejskich – stało się to w czasach, gdy powszechny był już system pozycyjny. Zatem polskie liczebniki dostosowane są już do struktury dziesiątkowego systemu pozycyjnego, a nie do analogii anatomicznych odwołujących się do liczenia na palcach dłoni i stóp.
- ↑ Od kilkudziesięciu lat w języku francuskim można zauważyć wypieranie tego dziedzictwa – np. liczba 80 (quatre-vingt), coraz częściej zastępowana jest nazwą octane.
Przypisy
- ↑ a b c d e f Gelman R., Gallistel C.R., The child’s understanding of number, Cambridge, MA: Harvard University Press, 1986.
- ↑ a b c d e f g h i j k l Szczygieł M., Cipora K., Hohol M., Liczenie na palcach w ontogenezie i jego znaczenie dla rozwoju kompetencji matematycznych, Psychologia Rozwojowa, 2015, tom 20, nr 3, s. 24.
- ↑ a b c d e f g h i j Szczygieł M., Cipora K., Hohol M., Liczenie na palcach w ontogenezie i jego znaczenie dla rozwoju kompetencji matematycznych, Psychologia Rozwojowa, 2015, tom 20, nr 3, s. 25.
- ↑ a b Fayol M., Seron X., About numerical representations: Insights from neuropsychological, experimental, and developmental studies, [w:] J.I. Campbell (red.), Handbook of Mathematical Cognition, s. 3–22, New York: Psychology Press, 2005.
- ↑ a b c d e f g h Cipora K., Szczygieł M., Hohol M., Palce, które liczą – znaczenie liczenia na palcach dla poznania matematycznego u człowieka dorosłego, 2014, Psycholgia-Etologia-Genetyka, Tom 30, s. 60.
- ↑ a b Andres M., Di Luca S., Pesenti M., Finger counting: The missing tool?, Behavioral and Brain Sciences, 2008, 31, 6, s. 642–643.
- ↑ Alibali M. W., DiRusso A.A., The function of gesture in learning to count: More than keeping track, Cognitive Development, 1999, 14, 1, s. 37–56.
- ↑ Geary D.G., Children’s mathematical development, research and practical applications, Washington 1994, American Psychological Association.
- ↑ Fuson K.C., Secada W.G., Teaching children to add by counting-on with one-handed finger patterns, Cognition and Instruction, 1986, 3, 3, s. 229–260.
- ↑ Ifrah 1990 ↓, s. 40.
- ↑ a b Butterworth B., The Mathematical Brain London, wyd. Macmillan, 1999.
- ↑ a b c d Semadeni Z., Matematyka w edukacji początkowej – podejście konstruktywistyczne.
- ↑ a b c Gruszczyk-Kolczyńska E., Dodawanie i odejmowanie w możliwie szerokim zakresie: od poziomu konkretów, przez zbiory zastępcze aż do rachowania w pamięci. Stosowanie tych umiejętności w rozwiązywaniu zadań, s. 167–186, [w:] Gruszczyk-Kolczyńska E. (red.), O dzieciach matematycznie uzdolnionych. Książka dla rodziców i nauczycieli, Warszawa 2012, Wydawnictwo Nowa Era.
- ↑ Domahs F., Moeller K., Huber S., Willmes K., Nuerk H.C., Embodied numerosity: Implicit handbased representations influence symbolic number processing across cultures, 2010, Cognition, 116, 2, s. 251–266.
- ↑ a b c d e f g h i j Szczygieł M., Cipora K., Hohol M., Liczenie na palcach w ontogenezie i jego znaczenie dla rozwoju kompetencji matematycznych, Psychologia Rozwojowa, 2015, tom 20, nr 3, s. 26.
- ↑ a b c d e f Domahs F., Krinzinger H., Willmes K., Mind the gap between both hands: Evidence for internal finger-based number representations in children’s mental calculation, 2008, Cortex, 44, 4, s. 359–367.
- ↑ a b c d e f g h K. Landerl, L. Kaufmann, Dyskalkulia, Wydawnictwo Harmonia, Gdańsk 2015, ISBN 978-83-7744-098-8, s. 82.
- ↑ a b c d K. Landerl, L. Kaufmann, Dyskalkulia, Wydawnictwo Harmonia, Gdańsk 2015, ISBN 978-83-7744-098-8, s. 84.
- ↑ a b c Kaufmann L., More evidence for the role of the central executive in retrieving arithmetic facts: A case study of severe developmental dyscalculia, Journal of Clinical and Experimental Neuropsychology, 2002 24, 3, s. 302–310.
- ↑ a b c d e f g h Cipora K., Szczygieł M., Hohol M., Palce, które liczą – znaczenie liczenia na palcach dla poznania matematycznego u człowieka dorosłego, 2014, Psycholgia-Etologia-Genetyka, Tom 30, s. 62.
- ↑ Jordan N.C., Kaplan D., Ramineni C., Locuniak M.N., Development of number combination skill in the early school years: When do fi ngers help?, Developmental Science, 2008, 11, 5, s. 662–668.
- ↑ a b c d e f g h Gruszczyk-Kolczyńska E., Zielińska E., Dziecięca matematyka: program dla przedszkoli, klas zerowych i placówek integracyjnych, Warszawa: WSiP, 1999.
- ↑ Moeller K., Martignon L., Wessolowski S., Engel J., Nuerk H.C., Effects of finger counting on numerical development – the opposing views of neurocognition and mathematics education, Frontiers in Psychology, 2011, 2, s. 75–79.
- ↑ a b c d e f Zaorska M., Rozwój kulturowy dziecka w koncepcji Lwa S. Wygotskiego, Acta Universitatis Nicolai Copernici, 2012, 28, s. 43.
- ↑ a b c Wiese H., Numbers, language and human mind, Cambridge 2003, Cambridge University Press.
- ↑ a b Rusconi E., Walsh V., Butterworth B., Dexterity with numbers: rTMS over left angular gyrus disrupts finger gnosis and number processing, Neuropsychologia, 2005, 43, 11, s. 1609–1624.
- ↑ a b c d e f g Nicoladis E., Pika S., Marentette P., Are number gestures easier than number words for preschoolers?, Cognitive Development, 2010, 25, 3, s. 247–261.
- ↑ a b c d e Cipora K., Szczygieł M., Hohol M., Palce, które liczą – znaczenie liczenia na palcach dla poznania matematycznego u człowieka dorosłego, 2014, Psycholgia-Etologia-Genetyka, Tom 30, s. 65.
- ↑ a b c d e f g h i j k l Szczygieł M., Cipora K., Hohol M., Liczenie na palcach w ontogenezie i jego znaczenie dla rozwoju kompetencji matematycznych, Psychologia Rozwojowa, 2015, tom 20, nr 3, s. 27.
- ↑ a b c d e Gracia-Bafalluy M., Noël M.P., Does finger training increase young children’s numerical performance?, 2008, Cortex, 44, 4, s. 368–375.
- ↑ Geary D.C., Bow-Thomas C.C., Liu F., Siegler R.S., Development of arithmetical competencies in Chinese and American children: Infl uence of age, language, and schooling, Child Development, 1996, 67, 5, s. 2022–2044.
- ↑ Fuson K.C., Kwon Y., Korean children’s understanding of multidigit addition and subtraction, 1992, Child Development, 63, 2, s. 491–506.
- ↑ Rusconi E., Pinel P., Dehaene S., Kleinschmidt A., The enigma of Gerstmann’s syndrome revisited: A telling tale of the vicissitudes of neuropsychology, Brain, 2010 133, 2, s. 320–332.
- ↑ a b c d e f g h i j k Szczygieł M., Cipora K., Hohol M., Liczenie na palcach w ontogenezie i jego znaczenie dla rozwoju kompetencji matematycznych, Psychologia Rozwojowa, 2015, tom 20, nr 3, s. 28.
- ↑ Poeck K., Phantoms following amputation in early childhood and in congenital absence of limbs, Cortex, 1965, 1, s. 269–275.
- ↑ a b c d Crollen V., Mahe R., Collignon O., Seron X., The role of vision in the development of finger–number interactions: Finger-counting and finger-montring in blind children, Journal of Experimental Child Psychology, 2011, 109, 4, s. 525–539.
- ↑ a b c Penner-Wilger M., Anderson M.L., An alternative view of the relation between finger gnosis and math ability: Redeployment of finger representations for the representation of number, Proceedings of the 30th annual meeting of the Cognitive Science Society, 2008, Austin, TX, s. 1647–1652.
- ↑ a b c Reeve R., Humberstone J., Five-to 7-year-olds’ finger gnosia and calculation abilities, Frontiers in Psychology, 2011, 2.
- ↑ a b c d e f Noël M.P., Finger gnosia: A predictor of numerical abilities in children?, Child Neuropsychology, 2005, 11, 5, s. 413–430.
- ↑ a b c d Fayol M., Barrouillet P., Marinthe C., Predicting arithmetical achievement from neuro-psychological performance: A longitudinal study, Cognition, 1998, 68, 2, s. B63–B70.
- ↑ a b c Marinthe C., Fayol M., Barrouillet P., Gnosies digitales et développement des performances arithméthiques, [w:] A. Van Hout, C. Meljac (red.), Troubles du calcule et dyscalculies chez l’enfant, Paris 2001, Masson, s. 239–254.
- ↑ a b c d Szczygieł M., Cipora K., Hohol M., Liczenie na palcach w ontogenezie i jego znaczenie dla rozwoju kompetencji matematycznych, Psychologia Rozwojowa, 2015, tom 20, nr 3, s. 29.
- ↑ a b c d e f Cipora K., Szczygieł M., Hohol M., Palce, które liczą – znaczenie liczenia na palcach dla poznania matematycznego u człowieka dorosłego, 2014, Psycholgia-Etologia-Genetyka, Tom 30, s. 63.
- ↑ a b c Tschentscher, N., Hauk, O., Fischer, M. H., Pulvermüller, F., You can count on the motor cortex: Finger counting habits modulate motor cortex activation evoked by numbers, Neuroimage, 2012, 59 (4), s. 3139–3148.
- ↑ a b c Cipora K., Szczygieł M., Hohol M., Palce, które liczą – znaczenie liczenia na palcach dla poznania matematycznego u człowieka dorosłego, 2014, Psycholgia-Etologia-Genetyka, Tom 30, s. 64.
- ↑ a b c d e K. Landerl, L. Kaufmann, Dyskalkulia, Wydawnictwo Harmonia, Gdańsk 2015, ISBN 978-83-7744-098-8, s. 81.
- ↑ a b Szczygieł M., Cipora K., Hohol M., Liczenie na palcach w ontogenezie i jego znaczenie dla rozwoju kompetencji matematycznych, Psychologia Rozwojowa, 2015, tom 20, nr 3, s. 23.
- ↑ Pesenti M., Thioux M., Seron X., De Volder A., Neuroanatomical substrates of Arabic number processing, numerical comparison, and simple addition: A PET study, Journal of Cognitive Neuroscience, 2000, 12, s. 461–479.
- ↑ Pinel P., Piazza M., Le Bihan D., Dehaene S., Distributed and overlapping cerebral representations of number, size, and luminance during comparative judgments, Neuron 41, 2004, nr 6, s. 983–993.
- ↑ Kaufmann L., Vogel S.E., Wood G., Kremser Ch., Schocke M., Zimmerhackl L.B., Koten J.W., A developmental fMRI study of non-symbolic numerical and spatial processing, Cortex, 2008, 44, s. 376–385.
- ↑ a b c d e f g h i j k l m n o p Kordos M., Wykłady z historii matematyki, Script, Warszawa 2010, s. 23–26.
- ↑ a b c d e f g h i Cipora K., Szczygieł M., Hohol M., Palce, które liczą – znaczenie liczenia na palcach dla poznania matematycznego u człowieka dorosłego, 2014, Psycholgia-Etologia-Genetyka, Tom 30, s. 61.
- ↑ Ifrah 1990 ↓, s. 48–49.
- ↑ Ifrah 1990 ↓, s. 51.
- ↑ Ifrah 1990 ↓, s. 47.
- ↑ a b Ifrah 1990 ↓, s. 39.
- ↑ a b James Chalmers, Vocabularies of the Bugilai and Tagota Dialects, British New Guinea, „The Journal of the Anthropological Institute of Great Britain and Ireland”, 27, 1898, s. 139–144, DOI: 10.2307/2842860, JSTOR: 2842860 (ang.).
- ↑ Ifrah 1990 ↓, s. 54.
- ↑ a b Ifrah 1990 ↓, s. 52.
- ↑ a b Cipora K., Szczygieł M., Hohol M., Palce, które liczą – znaczenie liczenia na palcach dla poznania matematycznego u człowieka dorosłego, 2014, Psycholgia-Etologia-Genetyka, Tom 30, s. 66.
- ↑ a b c d Cipora K., Szczygieł M., Hohol M., Palce, które liczą – znaczenie liczenia na palcach dla poznania matematycznego u człowieka dorosłego, 2014, Psycholgia-Etologia-Genetyka, Tom 30, s. 67.
- ↑ a b c d e f Cipora K., Szczygieł M., Hohol M., Palce, które liczą – znaczenie liczenia na palcach dla poznania matematycznego u człowieka dorosłego, 2014, Psycholgia-Etologia-Genetyka, Tom 30, s. 68.
- ↑ a b c d e f g Yutaka Nishiyama, Counting with the fingers, International Journal of Pure and Applied Mathematics, 2013, 85, 5, s. 859–868.
- ↑ a b c d e f g Ifrah 1990 ↓, s. 48.
- ↑ a b Ifrah 1990 ↓, s. 54–55.
- ↑ Ifrah 1990 ↓, s. 63–65.
- ↑ a b c Ifrah 1990 ↓, s. 71–72.
- ↑ a b c d Ifrah 1990 ↓, s. 62–63.
- ↑ a b c Ifrah 1990 ↓, s. 64.
- ↑ Ifrah 1990 ↓, s. 65.
- ↑ a b c d e f Ifrah 1990 ↓, s. 66–71.
- ↑ a b c d e f g h i j k l m n o Kolpas S.J., Let your fingers do the multiplying, Mathematics Teacher, 2002, 95, 4, s. 246–251.
Bibliografia
- Georges Ifrah: Dzieje liczby, czyli historia wielkiego wynalazku. Stanisław Hartman (tłum.). Wrocław: Zakład Narodowy im. Ossolińskich – Wydawnictwo, 1990. ISBN 83-04-03218-X.
Media użyte na tej stronie
Autor: Ragge Strand , Licencja: CC BY 4.0
Bildet er hentet fra Arkivverket.
Herren og hans tjenere, Nationaltheatret.
- Arkivinstitusjon : Riksarkivet
- Arkivnavn : Billedbladet NÅ
- Sted : Norge, Oslo, Oslo, Nationaltheatret
- Emneord: teater, skuespillere
- Avbildet:
Obscherasprostranenny medieval finger from the book "The amount of arithmetic" Luca Pacioli Italian mathematician / Общераспространённый средневековый пальцевый счёт из книги "Сумма арифметики" итальянского математика Луки Пачоли
Autor: Mariusz Swornóg, Licencja: CC BY-SA 4.0
liczenie na palcach (damskie dłonie)
Autor: Mariusz Swornóg, Licencja: CC BY-SA 4.0
liczenie na palcach (damskie dłonie)
Autor: Afghanistan Matters from Brunssum, Netherlands, Licencja: CC BY 2.0
A grade 3 year old counts with her fingers in the sun lit room of Murade Khane's primary school funded by Turquoise Mountain Foundation, Kabul.
Photo by Jacob Simkin of Australia.Autor: Mariusz Swornóg, Licencja: CC BY-SA 4.0
liczenie na palcach (damskie dłonie)
Autor: Mariusz Swornóg, Licencja: CC BY-SA 4.0
liczenie na palcach (damskie dłonie)
Finger counting symbols for number 604, according to Beda Venerabilis
Autor: Miguel Discart, Licencja: CC BY-SA 2.0
Warsaw (Poland)
(c) S. Krupp, CC BY-SA 3.0 de
Understanding each other; seen in a street near the bell tower of Xi'an, China
Autor: Рыцарь поля, Licencja: CC0
Russian duodecimal finger through the system (Русский пальцевый счёт двенадцатеричной системы)