Linia długa
Linia długa – linia transmisyjna przenosząca sygnały. Określenie stosowane przede wszystkim w teorii obwodów i technice mikrofal.
Linią długą jest każde urządzenie (pierwotnie linie przewodowe), w którym wymiar długości porównywalny jest z długością fali przebiegu elektrycznego rozchodzącego się w urządzeniu.
Przykładem linii długich są m.in. kable koncentryczne czy linia elektroenergetyczna napowietrzna wysokiego napięcia o znacznej długości (954 km).
W technice mikrofal definiuje się linię długą jako nieskończenie długą linię transmisyjną będącą idealnym odbiornikiem energii. W praktyce jest to linia transmisyjna o skończonej długości zakończona impedancją dopasowaną.
Linia długa jest charakteryzowana przez następujące parametry:
- R rezystancja jednostkowa linii [Ω/m],
- L indukcyjność jednostkowa linii [H/m],
- G konduktancja jednostkowa linii [S/m],
- C pojemność jednostkowa linii [F/m].
- Impedancja falowa linii:
- Stała propagacji:
Część rzeczywista to tzw. stała tłumienia wyr. w [Np/m], podawana też w [dB/m], zaś część urojona to stała fazowa wyr. w [rad/m]. jest pulsacją. Dla linii bezstratnych Prędkość fazowa fali w linii bezstratnej wynosi:
i jest zawsze mniejsza od prędkości światła w próżni Przykłady linii transmisyjnych (linie ciągłe są liniami sił pola elektrycznego E, zaś przerywane magnetycznego H, – względna przenikalność elektryczna i – względna przenikalność magnetyczna ośrodka o charakterze dielektryka lub magnetyka, który w linii pełni rolę izolatora):
Do najpopularniejszych należy linia koncentryczna. Ma ona tę zaletę, że linie pól elektrycznego i magnetycznego zamykają się wewnątrz linii.
Schemat zastępczy odcinka linii długiej o długości przedstawia poniższy rysunek:
Schemat ten wyjaśnia znaczenie parametrów jednostkowych linii.
Korzystając z prawa Ohma, można dla tegoż odcinka linii zapisać układ równań:
po przejściu do przyrostów infinitezymalnych (tj. dla nieskończenie małego ) otrzymać można:
co po podziałaniu na obydwie strony pierwszego z równań operatorem różniczkowania po długości i wstawieniu drugiego równania oraz podziałaniu na obydwie strony drugiego z równań operatorem różniczkowania po długości i wstawieniu pierwszego równania prowadzi w rezultacie do układu równań typu falowego opisujących zmiany napięć i prądów w linii transmisyjnej (tzw. równania telegrafistów). Jednoznaczne rozwiązania tego układu otrzymuje się przy ustalonym obciążeniu końca linii:
gdzie:
- – impedancja obciążająca,
zaś
- i
są odpowiednio napięciem i prądem na końcu linii (tj. dla ).
Rozwiązanie ma postać:
Z prawa Ohma wynika, że impedancja widziana w dowolnym punkcie linii (w miejscu odległym o :: od końca linii) wyniesie:
Dla linii bezstratnych zależność ta upraszcza się do postaci:
Z racji tego, że większość linii transmisyjnych można uznać z dobrym przybliżeniem za bezstratne, powyższa zależność ma kardynalne znaczenie przy obliczaniu parametrów wielu obwodów mikrofalowych działających w oparciu o teorię linii transmisyjnych. Jak widać impedancja linii zmienia się wraz z odległością od obciążenia stąd mówi się (w sensie impendancyjnym) o transformacyjnych własnościach linii. Trywialnym przypadkiem, jest obciążenie linii impedancją (przypadek idealnego dopasowania), dla którego w linii nic się nie zmienia i impedancja wejściowa na całej jej długości wynosi Można więc powiedzieć, że impedancja charakterystyczna linii to taka impedancja, że po obciążeniu nią linii prąd, napięcie, a co za tym idzie także impedancja wejściowa, utrzymują się wzdłuż linii na stałym poziomie. Stan dopasowania linii do obciążenia oznacza, że energia fali elektromagnetycznej propagującej się w linii w całości przedostaje się do obciążenia. W każdym innym przypadku mówi się o niedopasowaniu. Używa się dwóch miar dopasowania mających genezę w teorii odbicia fali elektromagnetycznej na granicy ośrodków:
- współczynnik odbicia – stosunek napięcia fali odbitej do napięcia fali padającej:
- współczynnik fali stojącej
W literaturze anglojęzycznej używa się oznaczenia SWR (standing wave ratio).
W zależności od stanu obciążenia linii długiej rozróżnia się następujące przypadki szczególne:
Impedancję wejściową w dowolnym miejscu linii długiej można określić korzystając z wykresu Smitha.
Transformacyjne własności linii przesyłowych wykorzystuje się przede wszystkim w technice mikrofal do konstrukcji obwodów dopasowujących takich jak stroiki i transformatory ćwierćfalowe, a także rezonatorów, sprzęgaczy kierunkowych, dzielników mocy, przełączników itd. Przykład wykorzystania linii transmisyjnych do konstrukcji oscylatora mikrofalowego stabilizowanego rezonatorem z akustyczną falą powierzchniową przedstawia poniższa fotografia (→[1]).
Bibliografia
- Stanisław Bolkowski: Teoria obwodów elektrycznych. Warszawa: Wydawnictwa Naukowo-Techniczne, 2001, s. 466–508. ISBN 83-204-2638-3.
- Jarosław Szóstka: Fale i anteny. Warszawa: Wydawnictwa Komunikacji i Łączności, 2001, s. 73–109. ISBN 83-206-1414-7.
Media użyte na tej stronie
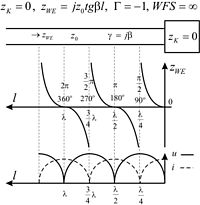
Zmiany napięcia i prądu w linii długiej zwartej na końcu
Zmiany napięcia i prądu w linii długiej obciążonej rezystancją (dwa przypadki)
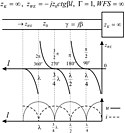
Zmiany napięcia i prądu w linii długiej obciążonej reaktancją indukcyjną
Autor: Wersję rastrową wykonał użytkownik polskiego projektu wikipedii: Mateusz Pasternak (MPasternak) ok. r. 1997, Zwektoryzował: Krzysztof Zajączkowski, Licencja: CC BY 2.5
Schemat zastępczy linii długiej
Autor: Wersję rastrową wykonał użytkownik polskiego projektu wikipedii: Mateusz Pasternak (MPasternak) ok. r. 1997, Zwektoryzował: Krzysztof Zajączkowski, Licencja: CC BY 2.5
Schemat linii dwuprzewodowej
Zmiany napięcia i prądu w linii długiej zwartej na końcu
Autor: Mateusz Pasternak, svg by Shape, Licencja: CC BY 2.5
Schemat budowy linii koncentrycznej
Schemat budowy niesymetrycznej linii paskowej
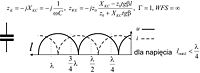
Zmiany napięcia i prądu w linii długiej obciążonej reaktancją pojemnościową
(c) MPasternak z polskiej Wikipedii, CC-BY-SA-3.0
oscylator wykonany techniką linii mikropaskowych