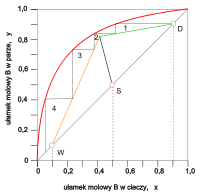
Metoda McCabe’a-Thielego

Dane do określania liczby stopni kolumny rektyfikacyjnej metodą McCabe’a i Thielego oraz wynik zastosowania metody

Metoda McCabe’a i Thielego – prosty graficzny sposób określania liczby półek teoretycznych kolumny rektyfikacyjnej, w której jest rozdzielana mieszanina dwuskładnikowa. Podstawą obliczeń są wyniki badań stanu równowagi ciecz–para oraz wyniki oznaczeń wielkości molowych strumieni destylatu i orosienia oraz stosunku stężeń obu składników w destylowanym roztworze (surowiec, surówka, ciecz surowa), orosieniu i destylacie.

Metoda została opracowana w 1925 przez doktorantów z Massachusetts Institute of Technology (MIT), Warrena L. McCabe’a i Ernesta W. Thielego^[1]. Jest stosowana w sytuacjach, gdy:

• molowe ciepła parowania składników surówki można uznać za jednakowe
• na każdy mol odparowującej cieczy kondensuje jeden mol pary
• przenikanie ciepła do i z kolumny destylacyjnej jest znikome

Podstawą metody jest bilans materiałowy procesu.

Przebieg wyznaczania liczby półek teoretycznych

Metoda McCabe’a i Thielego
krok po kroku (1)

W czasie destylacji roztworu A+B określa się ułamki molowe B w surówce (S), destylacie i cieczy wyczerpanej (W) oraz wielkość molowego strumienia (np. moli/h) destylatu i orosienia (R).

Jeżeli dane, dotyczące termodynamicznej równowagi ciecz-para w układzie A+B, nie są dostępne w piśmiennictwie, muszą być wykonane pomiary stężenia B w cieczy i w parze w stanie równowagi.

Dane dotyczące równowagi ciecz-para przedstawia się w układzie współrzędnych x_B – y_B

Wykreśla się linie określające skład surówki, destylatu i cieczy wyczerpanej.

Metoda McCabe’a i Thielego
krok po kroku (2)

Górną linię operacyjną wykreśla się pod kątem zależnym od wielkości orosienia

„Linię q” wykreśla się pod kątem zależnym od stanu surówki

Dolna linia operacyjna łączy dwa już wyznaczone punkty

Liczba „schodków” na linii prowadzonej między liniami operacyjnymi i linią równowagi odpowiada liczbie półek teoretycznych

Te same stężenia A i B w D i W można uzyskać w innych warunkach rektyfikacji

Przed rozpoczęciem oznaczenia liczby półek teoretycznych w określonej kolumnie rektyfikacyjnej trzeba uzyskać dane dotyczące równowagi ciecz–para w testowym układzie dwuskładnikowym A + B (B – składnik bardziej lotny). W czasie rektyfikacji roztworu testowego oznacza się wielkości strumieni destylatu i orosienia (liczba moli na godzinę) oraz stężenia składników w destylacie, surówce i cieczy wyczerpanej (ułamki molowe).

Sporządzany jest wykres w układzie współrzędnych:

• oś odciętych – x, ułamek molowy B w cieczy
• oś rzędnych – y, ułamek molowy B w parze

W pierwszej kolejności wykreśla się:

• linię pomocniczą x = y (przekątna kwadratu)
• linię równowagi – zależność ułamka molowego B w parze od ułamka molowego B w cieczy
• linie pionowe, określające ułamek molowy B w surówce, destylacie i cieczy wyczerpanej

W następnej kolejności wykreśla się tzw. górną linię operacyjną, dla tej części kolumny, która znajduje się nad punktem odpowiadającym składowi surówki (większe stężenie składnika bardziej lotnego). W tym celu z punktu przecięcia linii składu destylatu z linią pomocniczą x = y wykreśla się prostą o nachyleniu^[2][a]:

Δy / Δx = R / (D + R)

gdzie:

D – molowy strumień odbieranego destylatu (np. liczba moli na godzinę)

R – molowy strumień kondensatu zawracanego do kolumny, zwanego orosieniem.

Przykład:

orosienie: R = 2000 moli/h

destylat: D = 1000 moli/h

nachylenie linii operacyjnej: 2000 / (2000 + 1000) = 2/3 = 0,67

W kolejnym etapie jest wykreślana tak zwana „linia q”. Parametr q określa termodynamiczny stan surówki. Jest zdefiniowany jako ułamek molowy cieczy w surówce, która może być np. mieszaniną cieczy i pary, parą nasyconą bez cieczy lub cieczą o temperaturze niższej od temperatury wrzenia.

Współczynnik nachylenia „linii q” oblicza się jako:

Δy / Δx = q / (q - 1).

Przypadki charakterystyczne:

• surowiec jest cieczą o temperaturze wrzenia, nie zawierającą pary:

q = 1, Δy / Δx = nieskończoność, linia q jest równoległa do osi rzędnych (pionowa)

• surowiec jest parą nasyconą nie zawierającą cieczy:

q = 0, Δy / Δx = 0 , linia q jest równoległa do osi odciętych (pozioma)

• udziały cieczy i pary w surowcu są jednakowe:

q = 0,5 Δy / Δx = -1, linia q ma nachylenie 135o

W przypadkach, gdy surowiec jest przegrzaną parą lub ochłodzoną cieczą, z punktu przecięcia linii składu destylatu z linią x = y wykreśla się linie q najmniej odchylone od linii x = y, biegnące w górę (ochłodzona ciecz) lub w dół (nagrzana para).

Po wykreśleniu linii q przeprowadza się linię operacyjną dolną. Jest to prosta łącząca punkty przecięcia prostej x = y z linią q i z linią składu cieczy wyczerpanej.

Ostatnim etapem procedury jest wykreślenie krzywej schodkowej między liniami operacyjnymi i linią równowagi fazowej, rozpoczynając od punktu przecięcia prostej x = y z linią składu destylatu. Liczba uzyskanych stopni określa liczbę półek teoretycznych w badanej kolumnie.

Uwagi

Przypisy

Bibliografia

• Janusz Ciborowski: Podstawy inżynierii chemicznej. Warszawa: Wydawnictwo Naukowo-Techniczne, 1965, s. 515-530. (pol.).
• Janusz Ciborowski: Inżynieria chemiczna. Wyd. 2. Warszawa: Wydawnictwo Naukowo-Techniczne, 1955, s. 644-680. (pol.).

Linki zewnętrzne

• W. L. Mccabe, E. W. Thiele. Graphical Design of Fractionating Columns. „Ind. Eng. Chem.”, s. 605–611, czerwiec 1925. DOI: 10.1021/ie50186a023. (ang.). 
• Tore Haug-Warberg, Norwegian University of Science and Technology, Norway: Detailed discussion of McCabe-Thiele method. [dostęp 2015-02-18]. (ang.).
• Ming T. Tham: More detailed information on how to draw a McCabe-Thiele Diagram. [dostęp 2011-01-06]. (ang.).
• João Fernando Pereira Gomes. Reflections on the use of the McCabe and Thiele method. „Revista Ciências & Tecnologia”. 1 (1), s. 1–7, julho-dezembro 2007. Universidade Católica de Pernambuco. 
• McCabe-Thiele Diagram generator. [dostęp 2011-01-06]. (ang.).