Niestabilność Kelvina-Helmholtza

Symulacja numeryczna niestabilności Kelvina–Helmholtza

Niestabilność Kelvina-Helmholtza – zjawisko fizyczne zachodzące, gdy w jednorodnym płynie lub na granicy dwóch płynów występuje ścinanie. Zostało nazwane na cześć naukowców, którzy je opisali (byli to Lord Kelvin i Hermann von Helmholtz). Przykładem tej niestabilności jest powstawanie fal na wodzie, nad którą wieje wiatr. Niestabilność jest również obserwowana w chmurach, w głębi oceanu[1], w magnetosferze[2] i atmosferze Saturna[3], w otoczeniu Wielkiej Czerwonej Plamy na Jowiszu[4], a także w koronie słonecznej[5].

Teoria przewiduje powstanie niestabilności i przejście do przepływu turbulentnego w płynach o różnej gęstości, poruszających się z różnymi prędkościami. Helmholtz badał dynamikę dwóch cieczy o różnych gęstościach, kiedy na granicy łączącej płyny pojawiało się małe zaburzenie, takie jak fala.

Niestabilność Kelvina-Helmholtza manifestująca się w chmurach, w postaci formy zwanej fluctus[6], nad Mount Duval w Australii

Dla dostatecznie krótkich fal, jeśli pominie się napięcie powierzchniowe, powierzchnia dzieląca dwa płyny o różnej gęstości, poruszające się z równolegle skierowanymi i różnymi prędkościami jest niestabilna dla dowolnej prędkości. Napięcie powierzchniowe stabilizuje granicę płynów dla krótkich fal, dopóki nie zostanie przekroczona graniczna wartość prędkości, przewidywana przez teorię. Teoria uwzględniająca napięcie powierzchniowe przewiduje formowania się fal wywołane wiatrem nad wodą, po przekroczeniu przez wiatr pewnej prędkości jednak już Kelvin zdawał sobie sprawę, że ważną rolę w tym zjawisku odgrywa także lepkość cieczy[7]. W doświadczeniach nad powstawaniem fali nad wodą przy małej prędkości wiatru określono, że uporządkowane fale na wodzie powstają gdy powietrze porusza się z prędkością większą niż 6,3 m/s[7].

Niestabilność Kelvina-Helmholtza na styku dwóch pasów atmosfery Saturna
Fale Kelvina-Helmholtza na głębokości 500 m w Oceanie Atlantyckim

Dla ciągłego rozkładu gęstości i prędkości (z gęstością rosnącą w głąb, w związku z czym nie występuje niestabilność Rayleigha-Taylora), dynamikę niestabilności Kelvina-Helmholtza opisuje równanie Taylora-Goldsteina i powstanie niestabilności determinuje wartość bezwymiarowej liczby Richardsona, Ri. Typowo warstwa jest niestabilna dla Ri<0,25. Efekty te często występują w warstwach chmur[8]. Badania tej niestabilności mają zastosowanie w fizyce plazmy, na przykład przy syntezie z inercyjnym uwięzieniem plazmy[9].

Zobacz też


Przypisy

  1. ↑ William J. Broad: In Deep Sea, Waves With a Familiar Curl (ang.). The New York Times, 2010-04-19.
  2. ↑ Tamas I. Gombosi, Thomas P. Armstrong, Christopher S. Arridge, Krishan K. Khurana, Stamatios M. Krimigis, Norbert Krupp, Ann M. Persoon, Michelle F. Thomsen: Saturn’s Magnetospheric Configuration. W: Saturn from Cassini-Huygens. Michele Dougherty, Larry Esposito, Stamatios Krimigis (redaktorzy). Springer Science & Business Media, 2009, s. 247, 265. DOI: 10.1007/978-1-4020-9217-6_9. ISBN 1-4020-9217-2.
  3. ↑ Francis Reddy: Turbulent clouds and a rock-steadied ring (ang.). Astronomy magazine, 2004-10-26. [dostęp 2017-03-30]. [zarchiwizowane z tego adresu (2017-03-30)].
  4. ↑ Nezlin M.V., Snezhkin E.N., Trubnikov A.S. Kelvin-Helmholtz instability and the Jovian Great Red Spot. „[Soviet] Journal of Experimental and Theoretical Physics Letters”. 36, s. 190–193, 1982. Akademia Nauk ZSRR. Bibcode: 1982ZhPmR..36..190N (ang.). 
  5. ↑ Karen C. Fox: NASA’s Solar Dynamics Observatory Catches „Surfer” Waves on the Sun (ang.). NASA.
  6. ↑ Poznaj 12 zupełnie nowych chmur. Ich zdjęcia zapierają dech. twojapogoda.pl, 2017-03-24. [dostęp 2021-01-05].
  7. ↑ a b Anna Paquier, Frederic Moisy, Marc Rabaud. Surface deformations and wave generation by wind blowing over a viscous liquid. „Physics of Fluids”. 27 (12), s. 122103, 2015. DOI: 10.1063/1.4936395. 
  8. ↑ Lew Gramer: Kelvin-Helmholtz Instabilities (ang.). W: GFD-II [on-line]. 2007. [dostęp 2021-01-05].
  9. ↑ Bahman Zohuri: Inertial Confinement Fusion Driven Thermonuclear Energy. Springer, 2017, s. 190. ISBN 3-319-50907-1.

Bibliografia

  • William Thomson (Lord Kelvin). Hydrokinetic solutions and observations. „Philosophical Magazine”. 42, s. 362–377, 1871 (ang.). 
  • Hermann von Helmholtz. Über discontinuierliche Flüssigkeits-Bewegungen. „Monatsberichte der Königlichen Preussische Akademie der Wissenschaften zu Berlin”. 23, s. 215–228, 1868 (niem.). 

Media użyte na tej stronie

Wavecloudsduval.jpg
(c) GRAHAMUK z angielskojęzycznej Wikipedii, CC-BY-SA-3.0
Wave clouds forming over Mount Duval, NSW. Photograph by the author, donated to WP.
Deep Oceanic Kelvin-Helmholtz billows.jpg
Autor: Lgostiau, Licencja: CC BY-SA 3.0
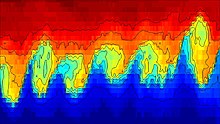
Temperature measured 530m deep, 15m off the bottom of the Great Meteor Seamount, North Atlantic Ocean, 2006

Horizontal scale (time) : 300s Vertical scale :13m

Color scale : 12.75-13.25 degree Celsius
Kelvin-Helmholtz Instability.ogv
Numerical Simulation of Kelvin-Helmholtz instability found in nature, fluid dynamics, physics, etc. Turbulent mixing of two different density fluids is caused by a velocity difference or shearing at the interface between the two.
Saturn Kelvin Helmholtz.jpg
A Kelvin-Helmholtz instability on Saturn, caused by the interaction between two bands of the planet's atmosphere. Image from the Cassini probe. Caption from NASA's press release: This turbulent boundary between two latitudinal bands in Saturn's atmosphere curls repeatedly along its edge in this Cassini image. This pattern is an example of a Kelvin-Helmholtz instability, which occurs when two fluids of different density flow past each other at different speeds. This type of phenomenon should be fairly common on the gas giant planets given their alternating jets and the different temperatures in their belts and zones. The image was taken with the Cassini spacecraft narrow angle camera on October 9, 2004, at a distance of 5.9 million kilometers (3.7 million miles) from Saturn through a filter sensitive to wavelengths of infrared light centered at 889 nanometers. The image scale is 69 kilometers (43 miles) per pixel.