Okno czasowe

Okno czasowe – funkcja opisująca sposób pobierania próbek z sygnału. Zakładając, że obserwowany jest pewien sygnał ${\displaystyle u(n)}$ w skończonym przedziale czasu, wtedy wynikiem tej obserwacji będzie sygnał:

${\displaystyle g(n)=u(n)w(n),\ -\infty <n<\infty ,}$

gdzie ${\displaystyle w(n)}$ jest właśnie funkcją okna.

Od postaci funkcji okna zależą różnice pomiędzy widmem sygnału obserwowanego ${\displaystyle u(n),}$ a widmem wyniku obserwacji ${\displaystyle g(n).}$ Istnieje wiele zdefiniowanych funkcji okna, kilka przykładowych przedstawiono poniżej.

Okna o wysokiej i umiarkowanie wysokiej rozdzielczości

Okno prostokątne

Okno prostokątne; B = 1,00

${\displaystyle w(n)=1}$

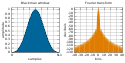
Okno Gaussa

Okno Gaussa; σ = 0,4; B = 1,45

${\displaystyle w(n)=e^{-{\frac {1}{2}}\left({\frac {n-(N-1)/2}{\sigma (N-1)/2}}\right)^{2}}}$

${\displaystyle \sigma \leqslant 0{,}5}$

Okno Hamminga

Okno Hamminga; α = 0,53836; β = 0,46164; B = 1,37

${\displaystyle w(n)=\alpha -\beta \;\cos \left({\frac {2\pi n}{N-1}}\right)}$

${\displaystyle w(n)=0{,}53836-0{,}46164\;\cos \left({\frac {2\pi n}{N-1}}\right)}$

Okno Hanna (Hanninga)

Okno Hanna (Hanninga); B = 1,50

${\displaystyle w(n)=0{,}5\left(1-\cos \left({\frac {2\pi n}{N-1}}\right)\right)}$

Okno Bartletta

Okno posiada zerowe wartości skrajnych elementów.

Okno Bartletta; L = N-1; B = 1,33

${\displaystyle w(n)=1-\left|{\frac {n-{\frac {N-1}{2}}}{\frac {L}{2}}}\right|}$

${\displaystyle L=N-1}$

${\displaystyle w(n)=1-\left|{\frac {n-{\frac {N-1}{2}}}{\frac {N-1}{2}}}\right|}$

Okno Trójkątne

Okno posiada niezerowe wartości skrajnych elementów.

Okno Trójkątne; L = N; B = 1,33

${\displaystyle w(n)=1-\left|{\frac {n-{\frac {N-1}{2}}}{\frac {L}{2}}}\right|}$

${\displaystyle L=N}$

${\displaystyle w(n)=1-\left|{\frac {n-{\frac {N-1}{2}}}{\frac {N}{2}}}\right|}$

Okno Bartletta-Hanna

Okno Bartletta-Hanna; B = 1,46

${\displaystyle w(n)=a_{0}-a_{1}\left|{\frac {n}{N-1}}-{\frac {1}{2}}\right|-a_{2}\cos \left({\frac {2\pi n}{N-1}}\right)}$

${\displaystyle a_{0}=0{,}62;\quad a_{1}=0{,}48;\quad a_{2}=0{,}38}$

Okno Blackmana

Okno Blackmana; α = 0,16; B = 1,73

${\displaystyle w(n)=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N-1}}\right)+a_{2}\cos \left({\frac {4\pi n}{N-1}}\right)}$

${\displaystyle a_{0}={\frac {1-\alpha }{2}};\quad a_{1}={\frac {1}{2}};\quad a_{2}={\frac {\alpha }{2}}}$

${\displaystyle \alpha =0{,}16}$

${\displaystyle a_{0}=0{,}42;\quad a_{1}=0{,}5;\quad a_{2}=0{,}08}$

Okno Kaisera

Okno Kaisera; α = 2; B = 1,7952

${\displaystyle w(n)={\frac {I_{0}{\Bigg (}\pi \alpha {\sqrt {1-({\tfrac {2n}{N-1}}-1)^{2}}}{\Bigg )}}{I_{0}(\pi \alpha )}}}$

Okna o niskiej rozdzielczości (ale o dużej dynamice)

Okno Nuttalla

Okno Nuttalla; z ciągłą pierwszą pochodna; B = 2,02

${\displaystyle w(n)=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N-1}}\right)+a_{2}\cos \left({\frac {4\pi n}{N-1}}\right)-a_{3}\cos \left({\frac {6\pi n}{N-1}}\right)}$

${\displaystyle a_{0}=0{,}355768;\quad a_{1}=0{,}487396;\quad a_{2}=0{,}144232;\quad a_{3}=0{,}012604}$

Okno Blackmana-Harrisa

Okno Blackmana-Harrisa; B = 2,0044

${\displaystyle w(n)=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N-1}}\right)+a_{2}\cos \left({\frac {4\pi n}{N-1}}\right)-a_{3}\cos \left({\frac {6\pi n}{N-1}}\right)}$

${\displaystyle a_{0}=0{,}35875;\quad a_{1}=0{,}48829;\quad a_{2}=0{,}14128;\quad a_{3}=0{,}01168}$

Okno Blackmana-Nuttalla

Okno Blackmana-Nuttalla; B = 1,9761

${\displaystyle w(n)=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N-1}}\right)+a_{2}\cos \left({\frac {4\pi n}{N-1}}\right)-a_{3}\cos \left({\frac {6\pi n}{N-1}}\right)}$

${\displaystyle a_{0}=0{,}3635819;\quad a_{1}=0{,}4891775;\quad a_{2}=0{,}1365995;\quad a_{3}=0{,}0106411}$

Okno Flat top

Ten rodzaj okna posiada najlepszą (w porównaniu z przedstawionymi wyżej funkcjami okna) dokładność odzwierciedlania amplitudy.

Okno Flat top; B = 3,7702

${\displaystyle w(n)=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N-1}}\right)+a_{2}\cos \left({\frac {4\pi n}{N-1}}\right)-a_{3}\cos \left({\frac {6\pi n}{N-1}}\right)+a_{4}\cos \left({\frac {8\pi n}{N-1}}\right)}$

${\displaystyle a_{0}=1;\quad a_{1}=1{,}93;\quad a_{2}=1{,}29;\quad a_{3}=0{,}388;\quad a_{4}=0{,}028}$