Oscylator anharmoniczny

Oscylator anharmoniczny – oscylator, którego okres drgań (w przeciwieństwie do oscylatora harmonicznego) zależy od jego amplitudy. W oscylatorze anharmonicznym, zależność energii potencjalnej od wychylenia z pozycji równowagi jest opisywana funkcją inną niż kwadratowa.

W mechanice klasycznej przykładem oscylatora anharmonicznego może być zwykłe wahadło fizyczne lub matematyczne, jednak dla małych wychyleń zachowują się one jak oscylatory harmoniczne.

W przypadku układów kwantowomechanicznych o oscylatorze anharmonicznym mówi się w sytuacjach, gdy do opisu danego stanu związanego nie wystarcza model oscylatora harmonicznego. W szczególności, oscylatorem anharmonicznym jest drgająca cząsteczka, zwłaszcza gdy rozważany zakres stanów energetycznych związanych z drganiami jest bliski energii dysocjacji. Intuicyjne zrozumienie przyczyn, dla których drgająca z dużą amplitudą cząsteczka nie może być oscylatorem harmonicznym, można osiągnąć odwołując się do najprostszego mechanicznego modelu cząsteczki, jakim jest układ dwóch kul połączonych sprężyną. Przy dużych odchyleniach od spoczynkowej długości sprężyny może nastąpić zetknięcie kulek (jeśli sprężyna jest skracana) lub rozerwanie sprężyny (jeśli jest ona rozciągana). Analogicznie, zbyt mała odległość jąder atomów w cząsteczce powoduje, że ich wzajemne siły odpychania są większe, niż gdyby utworzone przez te atomy wiązanie chemiczne było oscylatorem harmonicznym, zaś zbyt duża odległość jąder spowoduje dysocjację cząsteczki. Do matematycznego opisu oddziaływań międzyatomowych używa się m.in. potencjału Morse’a lub potencjału Lennarda-Jonesa.

Potencjał Morse’a

Porównanie potencjału Morse’a (niebieski) i potencjału oscylatora harmonicznego (zielony). Oscylator Morse’a odwzorowuje zmniejszanie się różnic energii między kolejnymi poziomami energii. Energia wiązania ${\displaystyle D_{e}}$ jest większa niż energia dysocjacji ${\displaystyle D_{0}}$ ze względu na niezerową energię poziomu zerowego drgań.

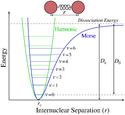
Jednym z przybliżeń anharmonicznego zachowania się oscylującego układu jest opisanie go za pomocą potencjału zaproponowanego przez Philipa Morse’a:

${\displaystyle V(r)=D_{e}(1-e^{-\alpha (r-r_{0})})^{2}+V(r_{0}),}$

gdzie:

${\displaystyle r_{0}}$ – odległość atomów molekuły w stanie równowagi,

${\displaystyle r}$ – odległość atomów molekuły po wychyleniu z położenia równowagi,

${\displaystyle D_{e}}$ – energia wiązania (głębokość "studni" wykresu V(r)),

${\displaystyle \alpha }$ – parametr opisujący szerokość "studni".

Oscylatora Morse’a używa się zazwyczaj do opisu molekuł. Dzięki takiemu podejściu możliwe staje się uwzględnienie procesu dysocjacji wiązania, gdyż wraz ze zwiększaniem się odległości atomów energia oddziaływania zbliża się asymptotycznie do zera. Model ten oddaje także zmniejszanie się różnic między kolejnymi poziomami energetycznymi molekuły w opisie kwantowym:

${\displaystyle E(v)=h\nu _{0}(v+1/2)-x_{e}h\nu _{0}(v+1/2)^{2},}$

gdzie:

${\displaystyle v}$ – kwantowa liczba oscylacji,

${\displaystyle \nu _{0}}$ – częstotliwość oscylatora harmonicznego,

${\displaystyle x_{e}}$ – stała anharmoniczności.

Stała anharmoniczności dana jest w przybliżeniu wzorem:

${\displaystyle x_{e}={\frac {\alpha ^{2}h}{2\mu \nu _{0}}}={\frac {h\nu _{0}}{4D_{e}}},}$

gdzie:

${\displaystyle \mu }$ – masa zredukowana cząsteczki

Potencjał Lennarda-Jonesa

Potencjał Lennarda-Jonesa dla dimeru argonu

Innym prostym modelem wprowadzającym możliwość dysocjacji wiązania jest potencjał wprowadzony przez Johna Lennarda-Jonesa. Dopuszcza on możliwość dysocjacji wiązania, wprowadza też odpychanie na małych odległościach. Składa się on z części repulsywnej ${\displaystyle \left({\frac {1}{r}}\right)^{12}}$ i atraktywnej ${\displaystyle \left({\frac {1}{r}}\right)^{6},}$ dając razem:

${\displaystyle V(r)=4\epsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right],}$

gdzie:

${\displaystyle \epsilon ,\sigma }$ ${\displaystyle \sigma }$ – parametry dobierane tak, aby kształt krzywej jak najbardziej odpowiadał modelowanemu układowi.

Zastosowania

Modele oscylatorów anharmonicznych używane są przy analizie widm oscylacyjnych (spektroskopia IR, spektroskopia Ramana), modelowaniu molekularnym, czy też opisie oscylatorów makroskopowych, gdzie stosowanie przybliżenia oscylatora harmonicznego byłoby niedopuszczalne.

Bibliografia

• Lucjan Piela: Idee Chemii Kwantowej. Warszawa: Wydawnictwo Naukowe PWN, 2003. ISBN 83-01-14000-3.

• Joanna Sadlej: Spektroskopia Molekularna. Warszawa: Wydawnictwa Naukowo-Techniczne, 2002. ISBN 83-204-2705-3.