Paradoks hydrostatyczny
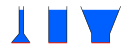
Paradoks hydrostatyczny – paradoks związany z mechaniką płynów, polegający na tym, że ciśnienie na dnie naczynia nie zależy wprost od ciężaru cieczy zawartej w naczyniu, a zależy od wysokości słupa cieczy nad dnem. Natomiast parcie cieczy na dno naczynia zależy od pola powierzchni dna, wysokości słupa cieczy i ciężaru właściwego cieczy. Wynika z tego, że parcie cieczy na dno w naczyniach o różnych kształtach będzie takie samo, jeżeli pole powierzchni dna każdego z tych naczyń i wysokość słupa cieczy w tych naczyniach będą równe.
Fakt ten, stwierdzony po raz pierwszy przez holenderskiego uczonego Simona Stevina w XVI w.[1][2], wydawał się wówczas paradoksalny, dlatego i dziś często nazywany jest paradoksem. Nazywany bywa także paradoksem Pascala, ponieważ Blaise Pascal w roku 1648 spopularyzował go demonstrując publicznie rozsadzenie beczki niewielką ilością wody. Doświadczenie to ilustrowało równocześnie prawo odkryte przez Pascala i nazwane jego imieniem[3][4].
Zobacz też
Przypisy
- ↑ Stevin Simon, Wisconstighe gedachtenissen. Deel 4: van de weeghconst, DBNL, 1605 [dostęp 2020-03-22].
- ↑ Simon Stevin, De beghinselen des waterwichts, Inde druckerye van Christoffel Plantijn, by Françoys van Raphelinghen, 1586 [dostęp 2020-03-22] (niderl.).
- ↑ Pascal B., Traitez de l'équilibre des liqueurs et de la pesanteur de la masse de l'air, Guillaume Desprez, 1663 [dostęp 2020-03-22].
- ↑ Pascal B., Traitez de l'équilibre des liqueurs, et de la pesanteur de la masse de l'air - Wielkopolska Biblioteka Cyfrowa, www.wbc.poznan.pl, 1698 [dostęp 2020-03-22].
Media użyte na tej stronie
Illustration zum "Hydrostatisches Paradoxon"
Illustration zum "Hydrostatisches Paradoxon"