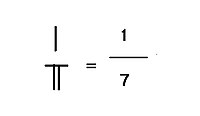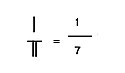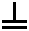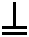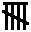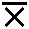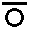Patyczki liczbowe
Patyczki do liczenia (chiń. upr. 籌; chiń. trad. 筹; pinyin chóu; jap. 算木, sangi) to małe pręciki, zwykle mające 3–14 cm długości, używane przez matematyków w Chinach, Japonii, Korei i Wietnamie. Są one rozkładane poziomo lub pionowo, aby przedstawić dowolną liczbę lub ułamek.
Zapis bazujący na ich ułożeniu nazywa się patyczki liczbowe. Jest to prawdziwie pozycyjny system liczbowy z cyframi od 1 do 9, a później także i 0.
Historia
Patyczki do liczenia były używane przez starożytnych Chińczyków od ponad dwóch tysięcy lat. W 1954 odnaleziono 40 patyczków z Okresu Walczących Królestw w Zuojiagongshan (左家公山) w Changsha w prowincji Hunan[1].
W 1973 archeolodzy odkryli kilka drewnianych skryptów w grobie z czasów dynastii Han w Hubei, na jednym z nich znajdowała się inskrypcja: „当利二月定算
”, jest to jeden z najwcześniejszych przykładów stosowania patyczków liczbowych w zapisie.
W 1976, pakiet kościanych patyczków z czasów Dynastii Han został odkryty w powiecie Qianyang w Shanxi.[2] Oznacza to, że patyczki musiały być używane także wcześniej; Laozi, w tekście z Okresu Walczących Królestw, powiedział „dobry kalkulator nie korzysta z patyczków”[3].
Gdy rozkwitła era abakusa, patyczki zostały porzucone, z wyjątkiem Japonii, gdzie rozwinięto z nich symboliczny zapis do algebry.
Sposób użycia
Patyczki liczbowe przedstawiają cyfry za pomocą ilości patyczków, przy czym prostopadłe patyczki oznaczają pięć. Aby uniknąć nieporozumień, poziome i pionowe formy są używane zamiennie. W ogólności, pionowe pręciki przedstawiają jednostki, setki, dziesiątki tysięcy, itd. Natomiast poziome oznaczają dziesiątki, tysiące, setki tysięcy itd. Sun Zi napisał, że „jeden jest pionowe, dziesięć jest poziome”[4][5]. Później kamień do gry w go był czasem używany do przedstawienia 0.
Zamienność form pionowych i poziomych jest bardzo istotna aby prawidłowo zrozumieć inskrypcje w rękopisach. Na przykład, w Licheng suanjin, 81 zapisano jako 
, a 108 zapisano jako 
; jasne jest, że na drugim umieszczono puste zero na „planszy do liczenia” (np.: podłodze lub macie), nawet jeśli w zapisie nie było odstępu. W tym samym rękopisie, 405 zapisano jako 
, z odstępem z oczywistych powodów, a nie ma sposobu, aby odczytać to jako „45” 
. Innymi słowy, zapisywane cyfry patyczkowe niekoniecznie muszą być pozycyjne, lecz na planszy do liczenia z pewnością są. jest dokładnym obrazem liczby patyczkowej na planszy.
Matematyk dynastii Song Jia Xian stosował ręcznie zapisane kolejno chińskie potęgi dziesiątki 步十百千万 jako wartość cyfry patyczkowej na zadanej pozycji, jak to wynika ze szkicu na stronie w Encyklopedii Cesarza Yongle. Ułożył on 七万一千八百二十四 (7 10000 1 1000 8 100 2 10 4) jako
七一八二四 7 1 8 2 4 万千百十步 10000 1000 100 10 krok
Potraktował on chińskie potęgi dziesiątki jako znaczniki pozycji, a 七一八二四 stały się pozycyjnymi cyframi dziesiętnymi. Następnie zapisał cyfry patyczkowe na pozycyjnych cyfrach dziesiętnych:
| 七 | 一 | 八 | 二 | 四 |
|---|---|---|---|---|
| 万 | 千 | 百 | 十 | 步 |
 |  |  |  |  |
W Japonii, matematycy umieszczali patyczki liczbowe na planszy do liczenia, arkuszu materiału z siatką, i używali jedynie pionowych form w oparciu o siatkę.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Pionowe |  |  |  |  |  |  |  |  |  | |
| Poziome |  |  |  |  |  |  |  |  |  |
| 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Pionowe | |  |  | | |  |  | |  | |
| Poziome |  |  |  | |  |  |  | |  |
Przykłady:
| 231 | | | | |
|---|---|---|---|---|
| 5089 | | | | |
| -407 | | | ||
| -6720 | | | |
Liczby patyczkowe
Liczby patyczkowe to pozycyjny system liczbowy utworzony z kształtów patyczków liczbowych. Liczby dodatnie zapisujemy wprost a ujemne z ukośnym słupkiem na ostatniej cyfrze. Pionowy słupek w poziomych formach 6–9 jest krótszy, aby zachować tę samą wysokość wszystkich znaków.
Okrąg (〇) reprezentuje 0. Wielu historyków myśli, że Gautama Siddha zapożyczył go od cyfr indyjskich w 718[4], lecz inni sądzą, że został utworzony od chińskiego wypełniacza miejsca na tekst „□”[6].
W XIII wieku matematycy Dynastii Song zmienili zapis cyfr dla 4, 5 i 9, aby zredukować liczbę kresek[6]. Nowa pozioma forma ostatecznie przekształciła się w cyfry Suzhou. Japończycy kontynuowali użycie form tradycyjnych.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Pionowe |  | | | | | | | | | |
| Poziome | | | | | | | |  |  |  |
| -0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Pionowe |  |  |  |  |  |  |  |  |  |  |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Pionowe | | | | |  |  | | | |  |
| Poziome | | | | | |  | | | |  |
Przykłady:
| Tradycyjny | Dynastia Song | |
|---|---|---|
| 231 | | |
| 5089 | | |
| -407 | | |
| -6720 | | |
Ułamki
Ułamki liczb patyczkowych są wyrażane jako dwie liczby patyczkowe jedna nad drugą (bez żadnych dodatkowych symboli jak współczesna kreska ułamkowa).
Unicode
Unicode 5.0 zawiera cyfry dla liczb patyczkowych w zarezerwowanym dla nich obszarze Supplementary Multilingual Plane (SMP) od U+1D360 do U+1D37F. Kody znaków dla cyfr poziomych 1-9 są w obszarze od U+1D360 do U+1D368, a ich odpowiedniki pionowe od U+1D369 do U+1D371. Te pierwsze to tzw. jednostki, a drugie dziesiątki[7], co jest sprzeczne z zasadami opisanymi wyżej. Zero należy przedstawiać za pomocą U+3007 (〇, ideographic number zero), a znak negacji jako U+20E5 (combining reverse solidus overlay)[8]. Jako że znaki te zostały umieszczone w zbiorze Unicode niedawno oraz z uwagi na to, że są dodane do SMP, ich dostępność w czcionkach może być mocno ograniczona. Szare obszary oznaczają kody nieprzypisane.
| Cyfry dla liczb patyczkowych diagram Unicode.org (PDF) | ||||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | |
| U+1D36x | 퍠 | 퍡 | 퍢 | 퍣 | 퍤 | 퍥 | 퍦 | 퍧 | 퍨 | 퍩 | 퍪 | 퍫 | 퍬 | 퍭 | 퍮 | 퍯 |
| U+1D37x | 퍰 | 퍱 | ||||||||||||||
Przypisy
- ↑ 中国独特的计算工具. [dostęp 2007-12-16]. [zarchiwizowane z tego adresu (2008-08-23)].
- ↑ Wu Wenjun ed, Grand Series of History of Chinese Mathematics, vol 1, p371
- ↑ 老子: 善數者不用籌策。
- ↑ a b Qīngxiáng Wáng: Sangi o koeta otoko (The man who exceeded counting rods). Tokyo: Tōyō Shoten, 1999. ISBN 4-88595-226-3.
- ↑ Chińskie Wikiźródło 正負術曰: 同名相除，異名相益，正無入負之，負無入正之。其異名相除，同名相益，正無入正之，負無入負之。
- ↑ a b Baocong Qian: Zhongguo Shuxue Shi (The history of Chinese mathematics). Beijing: Kexue Chubanshe, 1964.
- ↑ The Unicode Standard, Version 5.0 - Electronic edition. Unicode, Inc., 2006. s. 558.
- ↑ The Unicode Standard, Version 5.0 - Electronic edition. Unicode, Inc., 2006. s. 499–500.
Media użyte na tej stronie
Diagram of counting board in a Japanese drawing
An excerpt showing an example of counting rods for the number 71,824 by showing the Chinese numerals 七一八二四 and their respective place values 萬千百十步 above the number represented in counting rods.
This is a facsimile of the pages from the Katsuyo Sampo of en:Seki Kowa that tabulate the binomial coefficients and the Bernoulli numbers. Seki died in 1708, and the work was published in 1712, so it is in the public domain.
I obtained the file itself from the the web site of the Mathematical Association of America, here, then converted it from TIFF to PNG format.
The main portion of the table displays the binomial coefficients arranged in Pascal's triangle. The coefficients are written using rod numerals.
The bottommost row tabulates the Bernoulli numbers. The rightmost value is a special case, 全 ("everything"). Each of the other entries is either 空 (zero, literally, "empty") or a fraction n/d in the form d分之n. (See en:Chinese_numerals#Fractional_values for an elaboration of this notation.) There is a small double mark 二 in the margin before the denominatord and a small single mark 一 in the margin after the numerator n. So for example the fraction in the third column from the right (representing ) is written as 六分之一, which means 1/6; the fraction in the seventh column () is written 四十二分之一, which means 1/42. The sign is given by the characters under the marginal 一 mark, with 爲加 ("add") indicating positive values, and 爲減 ("reduce") indicating negative values.
The complete reading of the bottom row, right to left, is: "everything", 1/2, 1/6, 0, -1/30, 0, 1/42, 0, -1/30, 0, 5/66, 0.
—Dominus
Drawing of en:Pascal's Triangle published in 1303 by en:Zhu Shijie (1260-1320), in his Si Yuan Yu Jian. It was called Jia Xian triangle or Yanghui Triangle by the Chinese, after the mathematician en:Jia Xian and en:Yang Hui.
The fourth entry from the left in the second row from the bottom appears to be a typo (34 instead of 35, correctly given in the fifth entry in the same row).
