Pochodna cząstkowa

Pochodna cząstkowa – dla danej funkcji wielu zmiennych pochodna względem jednej z jej zmiennych przy ustaleniu pozostałych (w przeciwieństwie do pochodnej zupełnej, w której zmieniać się mogą wszystkie zmienne). Pochodne cząstkowe znajdują zastosowanie np. w rachunku wektorowym oraz geometrii różniczkowej.

Pochodne cząstkowe funkcji ${\displaystyle f}$ względem zmiennej ${\displaystyle x}$ oznacza się symbolami

${\displaystyle {\frac {\partial f}{\partial x}},\;f'_{x},\;f_{x}{\text{ lub }}\partial _{x}f.}$

Symbol pochodnej cząstkowej ∂^[a] ma wygląd zaokrąglonej litery „d”. Notacja ta, użyta po raz pierwszy przez Adriena-Marie Legendre’a, stała się powszechna po jej ponownym wprowadzeniu przez Carla Gustava Jakoba Jacobiego; z tej przyczyny bywa określana jako „delta Jacobiego”^[1].

Tradycyjnie mówi się, że notacja ${\displaystyle {\tfrac {\partial f}{\partial x}}}$ pochodzi od Gottfrieda Wilhelma Leibniza, zaś ${\displaystyle f'_{x}}$ to symbolika zaczerpnięta od Josepha Louisa Lagrange’a.

Wprowadzenie

Wykres funkcji ${\displaystyle z=f(x,y)=x^{2}+xy+y^{2}}$

Wartość z w zależności od x, dla y=1 ${\displaystyle (z=f(x)=x^{2}+x+1)}$

Niech ${\displaystyle f}$ będzie funkcją więcej niż jednej zmiennej. Przykładowo

${\displaystyle z=f(x,y)=x^{2}+xy+y^{2}.}$

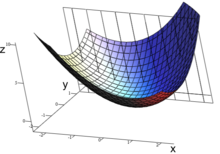
Wykres tej funkcji określa powierzchnię w przestrzeni euklidesowej. Istnieje nieskończenie wiele stycznych do każdego punktu tej powierzchni. Różniczkowanie cząstkowe polega na wybraniu jednej z tych prostych i uzyskaniu jej nachylenia. Zwykle najbardziej interesujące są proste, które są równoległe do płaszczyzny ${\displaystyle xz}$ czy ${\displaystyle yz.}$

Aby znaleźć nachylenie prostej stycznej do funkcji w ${\displaystyle (1,1,3),}$ która jest równoległa do płaszczyzny ${\displaystyle xz}$ należy traktować zmienną ${\displaystyle y}$ jak stałą. Wykres i wspomnianą płaszczyznę przedstawiono na rys. 1. Z kolei rys. 2. przedstawia wykres funkcji na płaszczyźnie ${\displaystyle y=1.}$ Szukając pochodnej wspomnianego równania przy założeniu, że ${\displaystyle y}$ jest stała, uzyskuje się nachylenie funkcji ${\displaystyle f}$ w punkcie ${\displaystyle (x,y,z),}$ którym jest

${\displaystyle {\frac {\partial z}{\partial x}}=2x+y.}$

W ten sposób okazuje się, poprzez podstawienie, że nachylenie w punkcie ${\displaystyle (1,1,3)}$ wynosi ${\displaystyle 3.}$ Dlatego

${\displaystyle {\frac {\partial z}{\partial x}}=3}$

w punkcie ${\displaystyle (1,1,3).}$ Innymi słowy pochodna cząstkowa ${\displaystyle z}$ względem ${\displaystyle x}$ w punkcie ${\displaystyle (1,1,3)}$ jest równa ${\displaystyle 3.}$

Definicja

Niech ${\displaystyle U}$ będzie otwartym podzbiorem przestrzeni euklidesowej ${\displaystyle \mathbb {R} ^{n}}$ i dane będą punkt ${\displaystyle \mathrm {a} =(a_{1},\dots ,a_{n})}$ oraz funkcja ${\displaystyle f\colon U\to \mathbb {R} .}$

Jeżeli istnieje skończona granica

${\displaystyle \lim _{h\to 0}{\frac {f(a_{1},\dots ,a_{k}+h,\dots ,a_{n})-f(a_{1},\dots ,a_{k},\dots ,a_{n})}{h}},}$

to nazywa się ją pochodną cząstkową funkcji ${\displaystyle f}$ w punkcie ${\displaystyle \mathrm {a} }$ względem zmiennej ${\displaystyle a_{k}}$ i oznacza jednym z wyżej wymienionych symboli.

Związek z pochodną zupełną

Jeżeli oznaczyć ${\displaystyle g(a_{k})=f(a_{1},\dots ,a_{k},\dots ,a_{n}),}$ to

${\displaystyle f'_{x}(a_{1},\dots ,a_{k},\dots ,a_{n})=\lim _{h\to 0}{\frac {g(a_{k}+h)-g(a_{k})}{h}}}$

jest po prostu pochodną ${\displaystyle g'(a_{k})}$ funkcji ${\displaystyle g.}$

Na przykład dla funkcji

${\displaystyle f(x,y)=x^{3}+3xy-y^{2}}$

można obliczyć pochodne cząstkowe względem zmiennych x i y:

${\displaystyle {\frac {\partial f}{\partial x}}(x,y)=f'_{x}(x,y)=3x^{2}+3y}$

${\displaystyle {\frac {\partial f}{\partial y}}(x,y)=f'_{y}(x,y)=3x-2y}$

Pochodne wyższych rzędów

Pochodne wyższych rzędów oblicza się, różniczkując znów po dowolnych zmiennych. Pochodne wyższych rzędów obliczane względem zmiennych różnych niż wybrana początkowo są znane jako pochodne mieszane^[2].

Pochodne czyste

${\displaystyle {\frac {\partial ^{2}f}{\partial x^{2}}}(x,y)=f''_{xx}(x,y)={\frac {\partial }{\partial x}}(3x^{2}+3y)=6x}$

${\displaystyle {\frac {\partial ^{2}f}{\partial y^{2}}}(x,y)=f''_{yy}(x,y)={\frac {\partial }{\partial y}}(3x-2y)=-2}$

i pochodne mieszane (różniczkowania zależnie od umowy należy wykonywać, tak jak w tym artykule, od lewej strony do prawej; bądź też, podobnie jak przy składaniu funkcji, od prawej do lewej)

${\displaystyle {\frac {\partial ^{2}f}{\partial x\partial y}}(x,y)=f''_{yx}(x,y)={\frac {\partial }{\partial x}}(3x-2y)=3}$

${\displaystyle {\frac {\partial ^{2}f}{\partial y\partial x}}(x,y)=f''_{xy}(x,y)={\frac {\partial }{\partial y}}(3x^{2}+3y)=3}$

Uogólnione twierdzenie Schwarza mówi, że jeśli wszystkie pochodne mieszane względem pewnych zmiennych są ciągłe w danym punkcie, ich wartość zależy wyłącznie od tego, względem których zmiennych różniczkujemy i ilekrotnie, natomiast nie zależy od kolejności w jakiej przeprowadza się różniczkowania.

Liczbę zastosowanych różniczkowań nazywamy rzędem pochodnej cząstkowej. Na przykład

${\displaystyle {\frac {\partial ^{2}f}{\partial x{}\partial y}}{(x,y)}}$

jest pochodną rzędu ${\displaystyle 2.}$

Pochodne cząstkowe wyższych rzędów zapisuje się także z użyciem notacji wielowskaźnikowej. Wtedy przez ${\displaystyle D^{\alpha }f,}$ gdzie ${\displaystyle \alpha =(\alpha _{1},\dots ,\alpha _{n})}$ jest wielowskaźnikiem rozumie się

${\displaystyle D^{\alpha }f(x_{1},\dots ,x_{n})={\frac {\partial ^{\alpha _{1}}}{\partial x_{1}}}\ldots {\frac {\partial ^{\alpha _{n}}}{\partial x_{n}}}f(x_{1},\dots ,x_{n}).}$

Rząd tej pochodnej cząstkowej wynosi oczywiście ${\displaystyle |\alpha |=\alpha _{1}+\ldots +\alpha _{n}.}$

Zobacz też

• dywergencja, rotacja
• gradient
• macierz Jacobiego
• operator Laplace’a
• operator d’Alemberta
• pochodna kierunkowa
• pochodna zewnętrzna
• pochodna zupełna

Uwagi

Przypisy

Bibliografia

• Witold Pogorzelski: Analiza matematyczna. T. II. Warszawa: Państwowe Wydawnictwo Naukowe, 1953, s. 10.