Prędkość

	Prędkość
	Prędkość
Rodzaj wielkości	wektorowa lub skalarna
Symbol
Jednostka SI	m/s
W podstawowych jednostkach SI
Inne jednostki	km/h, mph, ft/s
Wymiar

Prędkość – wielkość fizyczna opisująca szybkość zmiany położenia ciała względem układu odniesienia. Prędkość jest podstawową koncepcją kinematyki, gałęzi mechaniki klasycznej opisującej ruch ciał.

Prędkość może określać:

wektorową wielkość fizyczną wyrażająca zmianę wektora położenia w jednostce czasu,
skalarną wielkość oznaczającą przebytą drogę w jednostce czasu zwaną szybkością.

Jednostką prędkości w układzie SI jest metr na sekundę (m/s).

Definicje prędkości

Prędkość w ruchu prostoliniowym

Dla ruchu wzdłuż prostej prędkość definiuje się jako pochodną przesunięcia po czasie, czyli granicę przyrostów przesunięcia do przyrostu czasu w jakim nastąpił ten przyrost, dla nieskończenie małego przyrostu czasu:

v={\frac {\mathrm {d} x}{\mathrm {d} t}}=\lim _{\Delta t\to 0}{\frac {\Delta x}{\Delta t}}.

Prędkość ta zwana jest prędkością chwilową, w przeciwieństwie do prędkości średniej wyznaczonej dla dłuższego odcinka.

Prędkość wektorowa

Zmiana wektora położenia i tor ruchu

Zależności między wielkościami kinematycznymi

Prędkość wektorowa średnia określana jest jako iloraz zmiany wektora położenia do czasu, w jakim ta zmiana nastąpiła, co można określić wzorem^[1]:

\Delta {\vec {r}}={\vec {r}}_{B}-{\vec {r}}_{A},

{\vec {v}}_{s}={\frac {\Delta {\vec {r}}}{\Delta t}}.

Wynikającą z tego zmianę położenia określa wzór:

\Delta {\vec {r}}={\vec {v}}_{s}\cdot \Delta t.

Gdy odstęp czasu, w którym wyznacza się prędkość średnią, zmniejsza się, iloraz wektora zmiany położenia do czasu, w którym ta zmiana nastąpiła, dąży do pewnego wektora granicznego zwanego prędkością ciała w danym punkcie lub prędkością chwilową. Definicję tę można wyrazić wzorem^[1]:

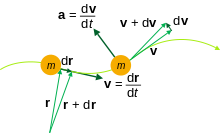
{\vec {v}}=\lim _{\Delta t\to 0}{\frac {\Delta {\vec {r}}}{\Delta t}}={\frac {d{\boldsymbol {r}}}{dt}}.

Prędkość jest pochodną wektora położenia względem czasu i jest wielkością wektorową, może być rozłożona na składowe, mające kierunek osi współrzędnych, podobnie wektor elementarnej zmiany położenia może być rozłożony na współrzędne^[1]

{\vec {v}}={\vec {v}}_{x}+{\vec {v}}_{y}+{\vec {v}}_{z}={\frac {d{\vec {x}}}{dt}}+{\frac {d{\vec {y}}}{dt}}+{\frac {d{\vec {z}}}{dt}}.

Wektor prędkości chwilowej jest równoległy do wektora zmiany położenia, przez co wektor prędkości chwilowej jest styczny do toru ruchu ciała^[1].

Prędkość jako wielkość niewektorowa

W wielu przypadkach prędkość rozumiana jest jako stosunek drogi do czasu jej przebycia. Tak jest rozumiana intuicyjnie, a także w wielu problemach fizycznych^[1]

v_{s}={\frac {\Delta s}{\Delta t}}.

Przy czym droga $s$ jest rozumiana jako długość odcinka krzywej (toru), po której porusza się ciało, od punktu początkowego do końcowego ruchu. Jeżeli prędkość zmienia się, to droga jest równa sumie małych odcinków drogi, na których uznaje się, że prędkość jest stała i jest określana jako prędkość chwilowa^[2]:

v=\lim _{\Delta t\to 0}{\frac {\Delta s}{\Delta t}}={\frac {ds}{dt}}.

Droga przebyta w niewielkim odcinku czasu, w którym prędkość nie zmienia się, jest proporcjonalna do prędkości i czasu. Droga przebyta gdy zmienia się prędkość może być obliczona jako suma, a w granicy jako całka, dróg na odcinkach, na których prędkość nie zmienia się:

S=\int \limits _{t_{0}}^{t_{1}}\;ds(t).

Stąd też prędkość średnia:

v_{s}={\frac {S}{t_{2}-t_{1}}}={\frac {\int \limits _{t_{0}}^{t_{1}}\;ds(t)}{t_{1}-t_{0}}}.

Prędkość chwilowa niewektorowa jest równa modułowi (wartości) prędkości chwilowej wektorowej^[2]

v=|{\vec {v}}|.

Średnia prędkość niewektorowa jest większa lub równa modułowi średniej prędkości wektorowej. Równość zachodzi tylko wtedy, gdy tor jest prostoliniowy

v_{s}={\frac {s}{t}}\geqslant |{\vec {v}}_{s}|.

Prędkość w różnych układach współrzędnych

Układ współrzędnych kartezjańskich

W układzie współrzędnych kartezjańskich trzy składowe prędkości (w przestrzeni) albo dwie (na płaszczyźnie) wyrażone są takimi samymi wzorami jak prędkości w ruchu prostoliniowym, przy czym drogą jest w tym przypadku współrzędna danej osi:

v_{x}={\frac {dx}{dt}}\qquad v_{y}={\frac {dy}{dt}}\qquad v_{z}={\frac {dz}{dt}}.

Prędkość można zapisać jako współrzędne wektora

{\vec {v}}=[v_{x},v_{y},v_{z}]

lub z użyciem wersorów osi

{\vec {v}}=v_{x}\cdot {\vec {i}}_{x}+v_{y}\cdot {\vec {i}}_{y}+v_{z}\cdot {\vec {i}}_{z}.

Wartość prędkości dana jest wzorem:

v={\sqrt {v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}}.

Układ współrzędnych biegunowych

Układ współrzędnych biegunowych na płaszczyźnie są dwie współrzędne, promień wodzący $(r)$ i amplituda punktu $(\varphi ),$ będąca kątem między wybranym kierunkiem a danym.

W układzie tym prędkość można określić poprzez transformację do kartezjańskiego układu współrzędnych o początku będącym początkiem układu biegunowego i zorientowanego względem zerowej amplitudy albo przez wyznaczenie kartezjańskiego układu współrzędnych o kierunku zgodnym z promieniem wodzącym. Transformacje określają wzory^[3]:

prędkość radialna – prędkość zmiany długości promienia wodzącego

v_{r}={\frac {dr}{dt}},

prędkość transwersalna – prędkość zmiany położenia w kierunku prostopadłym do promienia wodzącego

v_{\varphi }=r{\frac {d\varphi }{dt}},

Co można wyrazić przez prędkość kątową

\omega ={\frac {d\varphi }{dt}},

v_{\varphi }=r\omega ,

gdzie $\varphi$ jest kątem mierzonym od ustalonego kierunku.

Prędkość całkowita:

{\vec {v}}=v_{r}\cdot {\vec {i}}_{r}+v_{\varphi }\cdot {\vec {i}}_{\varphi }.

Wartość prędkości całkowitej^[3]:

v={\sqrt {v_{r}^{2}+v_{\varphi }^{2}}}={\sqrt {v_{r}^{2}+(r\omega )^{2}}}.

Układ współrzędnych walcowych

Układ współrzędnych walcowych, jest uogólnieniem układu biegunowego na przestrzeń trójwymiarową poprzez dodanie do współrzędnych biegunowych współrzędnej w kierunku osi z. Współrzędna z jest liniowa, odpowiadająca jej składowa prędkości jest równa:

v_{z}={\frac {dz}{dt}}.

Transformacja do kartezjańskich współrzędnych prędkości określa wzór:

{\vec {v}}=v_{r}\cdot {\vec {i}}_{r}+v_{\varphi }\cdot {\vec {i}}_{\varphi }+v_{z}\cdot {\vec {i}}_{z}.

Wartość prędkości:

v={\sqrt {v_{r}^{2}+v_{\varphi }^{2}+v_{z}^{2}}}.

Układ współrzędnych sferycznych

W układzie współrzędnych sferycznych położenie w przestrzeni opisane jest przez współrzędne: promień wodzący, długość azymutalna i odległość zenitalna $(r,\phi ,\theta ).$ Wprowadzając układ kartezjański o kierunkach osi zgodnych ze zmianami współrzędnych sferycznych, transformacja współrzędnych prędkości wyraża się wzorami:

v_{r}={\frac {dr}{dt}},

v_{\varphi }=r{\frac {d\varphi }{dt}},

v_{\theta }=r\sin \varphi \cdot {\frac {d\theta }{dt}},

gdzie:

\varphi

jest kątem mierzonym od ustalonego kierunku, np. od osi (OZ),

\theta

jest kątem, jaki tworzy rzut wektora wodzącego z ustalonym kierunkiem na płaszczyźnie prostopadłej do kierunku pierwszej osi (OZ). Tym kierunkiem może być oś OX.

Współrzędne prędkości w wyżej opisanym kartezjańskim układzie współrzędnych:

{\vec {v}}=v_{r}\cdot {\vec {i}}_{r}+v_{\varphi }\cdot {\vec {i}}_{\varphi }+v_{\theta }\cdot {\vec {i}}_{\theta }.

Moduł (wartość) prędkości:

v={\sqrt {v_{r}^{2}+v_{\varphi }^{2}+v_{\theta }^{2}}}.

Dowolne współrzędne krzywoliniowe

Z definicji prędkość $\mathbf {v}$ jest równa pochodnej promienia wodzącego $\mathbf {r}$ względem czasu: $\mathbf {v} ={\dot {\mathbf {r} }}.$ Aby wyrazić prędkość we współrzędnych krzywoliniowych, obliczamy tę pochodną według reguły różniczkowania funkcji złożonej, mając na uwadze, że promień wodzący $\mathbf {r}$ poruszającego się punktu można uważać za funkcję współrzędnych krzywoliniowych $q_{1},q_{2},q_{3}$ tego punktu, które z kolei są pewnymi funkcjami czasu t^[4]:

\mathbf {r} =\mathbf {r} (q_{1},q_{2},q_{3}),\quad q_{1}=q_{1}(t),\quad q_{2}=q_{2}(t),\quad q_{3}=q_{3}(t).

(1)

Stąd

\mathbf {v} ={\frac {d\mathbf {r} }{dt}}={\frac {\partial \mathbf {r} }{\partial q_{1}}}{\dot {q}}_{1}+{\frac {\partial \mathbf {r} }{\partial q_{2}}}{\dot {q}}_{2}+{\frac {\partial \mathbf {r} }{\partial q_{3}}}{\dot {q}}_{3}

(2)

oraz

v^{2}=\sum _{\sigma ,\,\rho =1}^{3}{\frac {\partial \mathbf {r} }{\partial q_{\sigma }}}{\frac {\partial \mathbf {r} }{\partial q_{\rho }}}{\dot {q}}_{\sigma }{\dot {q}}_{\rho },

(3)

gdzie wskaźniki $\sigma$ i $\rho$ przebiegają niezależnie od siebie wszystkie wartości od 1 do 3. W przypadku układu ortogonalnego jest^[4]

{\frac {\partial \mathbf {r} }{\partial q_{\sigma }}}{\frac {\partial \mathbf {r} }{\partial q_{\rho }}}=0

dla

q_{\sigma }\neq q_{\rho }

i dzięki temu

v^{2}=\sum _{\sigma =1}^{3}\left({\frac {\partial \mathbf {r} }{\partial q_{\sigma }}}\right)^{2}{\dot {q}}_{\sigma }^{2}.

(4)

Jeżeli promień wodzący $\mathbf {r}$ przedstawiony jest jako funkcja zmiennych $x,\,y,\,z,$ to wzory na prędkość $v^{2}$ przybiorą postać^[4]

v^{2}=\sum _{\sigma ,\,\rho =1}^{3}\left({\frac {\partial x}{\partial q_{\sigma }}}{\frac {\partial x}{\partial q_{\rho }}}+{\frac {\partial y}{\partial q_{\sigma }}}{\frac {\partial y}{\partial q_{\rho }}}+{\frac {\partial z}{\partial q_{\sigma }}}{\frac {\partial z}{\partial q_{\rho }}}\right){\dot {q}}_{\sigma }{\dot {q}}_{\rho },

(5)

v^{2}=\sum _{\sigma =1}^{3}\left[\left({\frac {\partial x}{\partial q_{\sigma }}}\right)^{2}+\left({\frac {\partial y}{\partial q_{\sigma }}}\right)^{2}+\left({\frac {\partial z}{\partial q_{\sigma }}}\right)^{2}\right]{\dot {q}}_{\sigma }^{2}.

(6)

Definicja wersorów: $\mathbf {e} _{1},\mathbf {e} _{2},\mathbf {e} _{3}$ osi $q_{1},q_{2},q_{3}$ wzorem

{\frac {\partial \mathbf {r} }{\partial q_{\sigma }}}=\left|{\frac {\partial \mathbf {r} }{\partial q_{\sigma }}}\right|\mathbf {e} _{\sigma },\quad \sigma =1,2,3.

(7)

Prędkość można teraz zapisać w postaci

\mathbf {v} =\sum _{\sigma =1}^{3}\left|{\frac {\partial \mathbf {r} }{\partial q_{\sigma }}}\right|{\dot {q}}_{\sigma }\mathbf {e} _{\sigma },

(8)

w której $|\partial \mathbf {r} /\partial q_{\sigma }|{\dot {q}}_{\sigma }$ jest składową prędkości $\mathbf {v}$ wzdłuż osi $q_{\sigma }.$

Prostopadły rzut prędkości $\mathbf {v}$ na oś $q_{\sigma }$ jest równy

v_{q_{\sigma }}^{ort}=\mathbf {v} \mathbf {e} _{\sigma }=\mathbf {v} {\frac {\partial \mathbf {r} /\partial q_{\sigma }}{|\partial \mathbf {r} /\partial q_{\sigma }|}}.

(8)

Ze wzoru (3) wynika równość

{\frac {\partial \mathbf {r} }{\partial q_{\sigma }}}={\frac {\partial \mathbf {v} }{\partial {\dot {q}}_{\sigma }}},

skąd wynika, że

\mathbf {v} {\frac {\partial \mathbf {r} }{\partial q_{\sigma }}}=\mathbf {v} {\frac {\partial \mathbf {v} }{\partial {\dot {q}}_{\sigma }}}={\frac {\partial (v^{2}/2)}{\partial {\dot {q}}_{\sigma }}}.

Rzut prostopadły prędkości określa wzór^[4]

v_{q_{\sigma }}^{ort}={\frac {\frac {\partial (v^{2}/2)}{\partial {\dot {q}}_{\sigma }}}{|\partial \mathbf {r} /\partial q_{\sigma }|}},\quad \sigma =1,2,3.

(9)

Związek z przyspieszeniem

Graficzna interpretacja zależności drogi i przyspieszenia od prędkości na wykresie prędkości od czasu.

Szybkość zmiany prędkości to przyspieszenie:

{\boldsymbol {a}}={\frac {d{\boldsymbol {v}}}{dt}}

Z zależności tej wynika wyrażenie na prędkość w zależności od przyspieszenia:

{\boldsymbol {v}}={\boldsymbol {v_{0}}}+\int {\boldsymbol {a}}\ dt

W ruchu prostoliniowym:

v=v_{0}+\int \limits _{t_{0}}^{t_{1}}a(t)dt

Na wykresie zależności prędkości od czasu chwilowe przyspieszenie ciała w danym momencie jest równe nachyleniu linii stycznej do krzywej w tym punkcie.

Prędkość kątowa

W ruchach krzywoliniowych definiowana jest prędkość kątowa

\omega ={\frac {d\varphi }{dt}},

gdzie $\varphi$ jest kątem obrotu wokół pewnej osi ustalonej osi. Traktując $\varphi$ jako kąt skierowany, można przypisać prędkości kątowej kierunek osi obrotu i zwrot zgodny z regułą śruby prawoskrętnej

{\vec {\omega }}={\frac {d{\vec {\varphi }}}{dt}}.

Tak zdefiniowana prędkość kątowa jest pseudowektorem. Pomiędzy prędkością kątową a prędkością transwersalną zachodzi następujący związek

{\vec {v}}_{\varphi }={\vec {\omega }}\times {\vec {r}}.

Przykłady prędkości w różnych rodzajach ruchów

Zmiany prędkości są podstawą klasyfikacji ruchów w fizyce.

Prędkość liniowa w ruchu jednostajnym prostoliniowym

Prędkość w ruchu jednostajnym prostoliniowym jest stała (zarówno jej kierunek i wartość). Przyjmuje się odtąd, że do położenia ciała wystarczy jedna współrzędna $x.$ Każdy ruch prostoliniowy można przez odpowiednie obroty układu współrzędnych, sprowadzić do przypadku jednowymiarowego. Prędkość w ruchu jednostajnym prostoliniowym określa więc następująca zależność:

{\vec {v}}={\frac {\Delta {\vec {r}}}{\Delta t}}={\frac {x(T)-x(0)}{T}}{\vec {i}}_{x},

|{\vec {v}}|={\frac {x(T)-x(0)}{T}}={\frac {S}{T}}={\textrm {const}},

gdzie:

{\vec {r}}(t)

– wektor położenia jako funkcja czasu

t,

S

– przebyta droga,

T

– czas trwania ruchu,

x(t)

– funkcja położenia (skalar) od czasu.

Prędkość liniowa w ruchu jednostajnie przyspieszonym

Przyspieszenie ${\vec {a}}$ jest stałe i niezerowe, więc prędkość ${\vec {v}}$ zmienia się. W ruchu tym także można ograniczyć się do rozpatrywania jednej współrzędnej.

{\vec {a}}={\frac {\Delta {\vec {v}}}{\Delta t}}\quad \to \quad \Delta {\vec {v}}={\vec {a}}\Delta t,

{\vec {v}}(T)-{\vec {v}}(0)={\vec {a}}T\quad \to \quad {\vec {v}}(T)={\vec {v}}(0)+{\vec {a}}T,

gdzie:

T

– całkowity czas ruchu,

{\vec {v}}(t)

– wektor prędkości jako funkcja czasu.

Czasem (zazwyczaj z powodów dydaktycznych) wyróżnia się specjalny przypadek ruchu jednostajnie przyspieszonego prostoliniowego – ruch jednostajnie opóźniony prostoliniowy. W ruchu tym wektor przyspieszenia ${\vec {a}}$ jest stały i skierowany przeciwnie do wektora prędkości ${\vec {v}}(t).$

Ruch jednostajny po okręgu (prędkość kątowa)

W tym ruchu wektor prędkości kątowej ${\vec {\omega }}$ jest stały i jego wartość wyraża się wzorem:

\omega ={\frac {\Delta \phi }{t}}.

Prędkość w ruchu po okręgu też jest stała i wiąże się z prędkością kątową wzorem

v=\omega r.

Znajomość prędkości kątowej umożliwia zapisanie równań ruchu po okręgu we współrzędnych kartezjańskich

x(t)=r\cos \omega t,

y(t)=r\sin \omega t.

Zobacz też

Przypisy

↑ ^a ^b ^c ^d ^e Wróblewski i Zakrzewski 1984 ↓, s. 84.
↑ ^a ^b Wróblewski i Zakrzewski 1984 ↓, s. 84–86.
↑ ^a ^b JerzyJ. Kwela JerzyJ., Mechanika klasyczna i relatywistyczna, Gdańsk: Wydawnictwo Uniwersytetu Gdańskiego, 2010, ISBN 978-83-7326-703-9 [dostęp 2019-08-19] [zarchiwizowane z adresu 2019-08-19] .
↑ ^a ^b ^c ^d G.K. Susłow, Mechanika teoretyczna, PWN, Warszawa 1960.

Bibliografia

Andrzej Kajetan Wróblewski, Janusz A. Zakrzewski: Wstęp do fizyki. Warszawa: Państwowe Wydawnictwo Naukowe, 1984. ISBN 83-01-01359-1.

[CITEREFWróblewskiZakrzewski198484-1] Wróblewski i Zakrzewski 1984 ↓, s. 84.

[CITEREFWróblewskiZakrzewski198484–86-2] Wróblewski i Zakrzewski 1984 ↓, s. 84–86.

[kwela-3] JerzyJ. Kwela JerzyJ., Mechanika klasyczna i relatywistyczna, Gdańsk: Wydawnictwo Uniwersytetu Gdańskiego, 2010, ISBN 978-83-7326-703-9 [dostęp 2019-08-19] [zarchiwizowane z adresu 2019-08-19] .

[Sus-4] G.K. Susłow, Mechanika teoretyczna, PWN, Warszawa 1960.

[1]

[2]

[3]

[4]

Działy	Dynamika Kinematyka Mechanika nieba Mechanika ośrodków ciągłych Mechanika statystyczna Mechanika stosowana Statyka
Sformułowania	Formalizm Hamiltona Formalizm Lagrange’a Mechanika newtonowska
Koncepcje podstawowe	Bezwładność Czas Energia Energia kinetyczna Energia potencjalna Grawitacja Masa Moc Moment bezwładności Moment pędu Moment siły / Moment / Para sił Popęd Praca Praca wirtualna Przestrzeń Przyspieszenie Prędkość Pęd Siła Szybkość Układ odniesienia Zasada d’Alemberta
Podstawowe zagadnienia	Bryła sztywna Dynamika bryły sztywnej Siła Coriolisa Kinematyczne równanie ruchu Oscylator harmoniczny Nieinercjalny układ odniesienia Oś obrotu Prawo powszechnego ciążenia Przemieszczenie Przyspieszenie kątowe Prędkość kątowa Prędkość obrotowa Pulsacja Ruch Ruch harmoniczny Ruch jednostajny prostoliniowy Ruch obrotowy Równania Eulera (dynamika bryły sztywnej) Siła bezwładności Siła dośrodkowa Siła odśrodkowa Tarcie Tłumienie Inercjalny układ odniesienia Wahadło Wibracje Zasady dynamiki Newtona
Znani uczeni	Jean le Rond d’Alembert Alexis Clairaut Leonhard Euler Galileusz William Rowan Hamilton Jeremiah Horrocks Joseph Louis Lagrange Pierre Simon de Laplace Pierre Louis Maupertuis Isaac Newton Henri Poincaré Siméon Denis Poisson

Navigation

Nawigacja

Portale tematyczne

Prędkość

Spis treści

Definicje prędkości

Prędkość w ruchu prostoliniowym

Prędkość wektorowa

Prędkość jako wielkość niewektorowa

Prędkość w różnych układach współrzędnych

Układ współrzędnych kartezjańskich

Układ współrzędnych biegunowych

Układ współrzędnych walcowych

Układ współrzędnych sferycznych

Dowolne współrzędne krzywoliniowe

Związek z przyspieszeniem

Prędkość kątowa

Przykłady prędkości w różnych rodzajach ruchów

Prędkość liniowa w ruchu jednostajnym prostoliniowym

Prędkość liniowa w ruchu jednostajnie przyspieszonym

Ruch jednostajny po okręgu (prędkość kątowa)

Zobacz też

Przypisy

Bibliografia

Media użyte na tej stronie