Przeniesienie równoległe

Przeniesienie równoległe wektora po sferze wzdłuż trójkąta geodezyjnego. Długość i kąt jaki wektor tworzy z każdym z odcinków pozostają stałe podczas przenoszenia. kąt skręcenia wektora ${\displaystyle \alpha }$ jest proporcjonalny do pola trójkąta.

Przeniesienie równoległe (transport równoległy) – przeniesienie wielkości geometrycznych (wektorów, w ogólności tensorów) wzdłuż krzywej regularnej na danej rozmaitości. Zakłada się, że wektor jest przenoszony równolegle, jeżeli zachowuje stały kąt względem linii geodezyjnej na danej rozmaitości. Warunkiem koniecznym i dostatecznym tak pojętego przenoszenia równoległego jest zerowanie się pochodnej kowariantnej przenoszonego wektora, liczonej wzdłuż krzywej, wzdłuż której wektor jest przenoszony.

Wprowadzenie pojęcia przeniesienia równoległego wektorów stycznych do krzywej stanowiło ważny etap w rozwoju geometrii różniczkowej, który wniósł Levi-Civita.

Przeniesienie równoległe wektora

Mając daną krzywą można przenosić wzdłuż niej wektory w różny sposób – zależy to od założonego rodzaju przestrzeni, do której należy krzywa, a tym samym od postaci tensora metrycznego tej przestrzeni. Postać tensora metrycznego implikuje bowiem równania linii geodezyjnych w danej rozmaitości.

Przestrzeń euklidesowa

• W przestrzeni euklidesowej liniami geodezyjnymi są proste euklidesowe – przeniesienie równoległe wektora odbywa się wzdłuż linii prostej lub łamanej, złożonej z odcinków prostej i polega na przesuwaniu wektora z zachowaniem jego długości oraz kąta nachylenia do prostej do kolejno pokonywanych odcinków łamanej.
• Jeżeli przenoszenie odbywa się wzdłuż innej krzywej, np. wzdłuż okręgu, to trzeba krzywą przybliżyć łamaną o bardzo małych odcinkach prostoliniowych – i postępować jak omówiono wyżej.

Dowolna rozmaitość

Rozważmy dowolną rozmaitość riemannowską (np. na powierzchnię sfery, torus itd.). Geodezyjne pełnią tu tę samą rolę, jak proste na płaszczyźnie euklidesowej czy w przestrzeni euklidesowej, tj. są najkrótszymi liniami, łączącymi dane dwa punkty. Przeniesienie równoległe wzdłuż linii geodezyjnej można opisać w analogii do przeniesienia równoległego wektora na płaszczyźnie euklidesowej.

• Jeżeli przenoszenie wektora odbywa się wzdłuż krzywej geodezyjnej właściwej dla danej powierzchni lub wzdłuż łamanej, złożonej z fragmentów krzywych geodezyjnych, to zasady przenoszenia są identyczne jak w przestrzeni euklidesowej – geodezyjne są „prostymi” na powierzchniach analogicznymi do prostych w płaszczyźnie euklidesowej; zatem wektor jest przenoszony równoległe z zachowaniem stałej długości i stałego kąta nachylenia do wektora stycznego do geodezyjnej lub do kolejnych odcinków łamanej geodezyjnej.
• Dla dowolnej krzywej, która nie jest geodezyjną, proces transportu musi być zmodyfikowany poprzez przybliżenie krzywej łamaną geodezyjną.

Przenoszenie równoległe a metryka

Przesuwanie równoległe wektora według procedury Leviego-Civity

Transport zadany metryką ${\displaystyle ds^{2}=dr^{2}+d\varphi ^{2}.}$

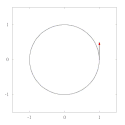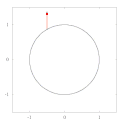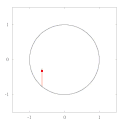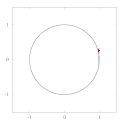
Rysunki obok pokazują transport równoległy Leviego-Civity dla dwóch różnych 2-wymiarowych przestrzeni Riemanna, które są zdefiniowane pokazanymi tam różnymi metrykami.

(1) Na pierwszym rysunku zadana jest metryka

${\displaystyle ds^{2}=dr^{2}+d\varphi ^{2}.}$

Metryka ta implikuje, iż liniami geodezyjnymi są okręgi; dlatego wektor przenoszony równolegle zachowuje stały kąt względem okręgu. Rozmaitość ta nie jest więc rozmaitością euklidesową.

(2) Na drugim rysunku zadana jest metryka

${\displaystyle ds^{2}=dr^{2}+r^{2}d\varphi ^{2}.}$

Jest to metryka indukowana przez układ współrzędnych biegunowych, wprowadzonych na płaszczyźnie euklidesowej. Mimo że współrzędne są krzywoliniowe, to metryka ta implikuje, iż geodezyjne są prostymi euklidesowymi. Dlatego wektor przenoszony równolegle zachowuje stały kąt względem każdej prostej euklidesowej (np. względem linii pionowej).

Przesuwanie równoległe wektora według procedury Leviego-Civity

Transport zadany metryką ${\displaystyle ds^{2}=dr^{2}+r^{2}d\varphi ^{2}.}$

Mając daną krzywą można więc przenosić wzdłuż niej wektory w różny sposób – zależnie od założonej postaci przestrzeni, do której należy krzywa, a tym samym od postaci założonego tensora metrycznego. Mianowicie:

(1) jeżeli daną krzywą traktuje się jako rozmaitość 1-wymiarową, to tensor metryczny jest zadany macierzą 1 × 1,

(2) jeżeli zakłada się, iż dana krzywa należy do powierzchni 2-wymiarowej, to tensor metryczny jest zadany macierzą 2 × 2,

(3) jeżeli zakłada się, iż dana krzywa należy do przestrzeni 3-wymiarowej, to tensor metryczny jest zadany macierzą 3 × 3,

(4) jeżeli zakłada się, iż dana krzywa należy do przestrzeni 4-wymiarowej, to tensor metryczny jest zadany macierzą 4 × 4 (np. linia świata cząstki w przestrzeni pseudoeuklidesowej 4-wymiarowej, opisanej tensorem metrycznym Minkowskiego).

Wybór metryki a opis ruchu ciał

Jeżeli chce się opisać rzeczywisty ruch ciał, to równania ruchu muszą uwzględniać faktyczną postać tensora metrycznego czasoprzestrzeni. Dlatego np. ogólna teoria względności formułuje równania ruchu ciał zakładając, że ciała poruszają się po liniach geodezyjnych, wyznaczonych przez przeniesienie równoległe właściwe dla metryki, która zależy m.in. od rozkładu materii i energii w przestrzeni (por. równania Einsteina).

Definicja formalna przeniesienia

Dokładniej proces transportu można opisać odwołując się do krzywizny geodezyjnej, która mierzy, jak bardzo krzywa odchyla się od geodezyjnej. Mianowicie, pole wektorowe ${\displaystyle v(t)}$ krzywej ${\displaystyle c(t)}$ o jednostkowej prędkości, z krzywizną geodezyjną ${\displaystyle k_{g}(t),}$ jest równoległe wzdłuż krzywej jeżeli

• pole to ma stałą długość
• kąt ${\displaystyle \theta (t)}$ jaki pole tworzy z wektorem prędkości ${\displaystyle c(t)}$ spełnia warunek

  ${\displaystyle {\dot {\theta }}(t)=-k_{g}(t).}$

Niech ${\displaystyle \nabla }$ będzie pochodną kowariantną na rozmaitości ${\displaystyle M,}$ zaś ${\displaystyle \gamma :[a,b]\to M}$ krzywą gładką. Pole wektorowe ${\displaystyle X}$ wzdłuż krzywej ${\displaystyle \gamma (t)}$ nazywamy równoległym, gdy znika pochodna kowariantna

${\displaystyle \nabla _{d/dt}X=0.}$

Z teorii układów równań różniczkowych zwyczajnych wynika, że dla każdego wektora ${\displaystyle v\in T_{\gamma (a)}M}$ istnieje dokładnie jedno pole ${\displaystyle X_{v}}$ wzdłuż ${\displaystyle \gamma ,}$ równoległe i takie, że ${\displaystyle X_{v}(a)=v.}$ Oczywistym jest, że pole zerowe jest równoległe i liniowa kombinacja (o stałych współczynnikach) pól równoległych jest polem równoległym.

Zobacz też

• pochodna kowariantna
• połączenie Leviego-Civity

Bibliografia

• L.D. Landau, E.M. Lifszyc: Teoria pola. Warszawa: PWN, 2009.
• P.W. Walczak, Wstęp do geometrii różniczkowej, 2004, dostęp 2012-06-28.

Linki zewnętrzne

• Lecture 8: Parallel Transport & Curvature (International Winter School on Gravity and Light 2015):