Przestrzeń fazowa
Przestrzeń fazowa (przestrzeń stanów) – przestrzeń przypisana do danego układu dynamicznego; osie współrzędnych reprezentują różne wielkości fizyczne (w ogólności np. współrzędne uogólnione i pędy uogólnione), pozwalające jednoznacznie opisać stanu tego układu, tzn. każdy punkt przestrzeni fazowej przedstawia jeden możliwy stan układu.
W mechanice klasycznej przestrzeń stanów układu cząstek materialnych jest reprezentowana przez położenia i pędy poszczególnych cząstek. Np. stan jednej cząstki w przestrzeni jest określony w pełni, jeżeli są dane współrzędne położenia i współrzędne pędu cząstki, tj..
W termodynamice przestrzeń stanów stałej porcji substancji jest reprezentowana przez ciśnienie i temperaturę (lub ciśnienie i objętość, itd.).
Koncepcja przestrzeni stanów rozwinęli w późnych latach XIX-tego wieku Ludwig Boltzmann, Henri Poincaré oraz Josiah Willard Gibbs.
Jeżeli układ zmienia swój stan w czasie, to kreśli w przestrzeni stanów krzywą zwaną trajektorią, krzywą fazową lub orbitą.
Liczba wymiarów przestrzeni stanów
Przestrzeń stanów jest wielowymiarowa:
- każdy stopień swobody układu mechanicznego jest opisywany za pomocą współrzędnej kartezjańskiej lub współrzędnej uogólnionej; każdej współrzędnej odpowiada osobny wymiar przestrzeni,
- ponadto dochodzą wymiary związane z prędkościami lub prędkościami uogólnionymi (czyli zmianami współrzędnych uogólnionych w czasie); zamiast prędkości używa się też pędów.
Przykłady
- Dla cząstki poruszającej się w jednym kierunku przestrzeń stanów ma dwa wymiary, odpowiadające położeniu i prędkości cząstki.
- Dla 1 mola gazu rzeczywistego wymiar przestrzeni stanów możemy oszacować w następujący sposób: przy 1 molu gazu (w przybliżeniu 6×1023 cząstek), zadając dla każdej cząstki kolejno 3 wymiary związane z jej położeniem, 3 ze składowymi prędkości wzdłuż każdej osi, a także wymiary związane z drganiami cząsteczki, jej obrotami w przestrzeni jak i obrotami składowych elementów cząstki wokół osi wiązania, otrzymujemy zestaw wymiarów w przestrzeni rzędu 1024 - 1025.
Przestrzeń stanów w fizyce klasycznej
W fizyce klasycznej ze znajomości położenia i prędkości układu można wyliczyć stan układu w dowolnej chwili w przyszłości i przeszłości. Oznacza to, że ewolucja układu jest w pełni zdeterminowana. Ruchowi takiego układu odpowiada w przestrzeni fazowej trajektoria złożona z kolejnych stanów, jakie układ zajmował lub będzie zajmował z upływem czasu. Z kształtu trajektorii można poznać różne własności układu, co jest szczególnie przydatne w analizie układów złożonych. Własnością trajektorii deterministycznych jest, że wzajemnie się nie przecinają.
Gdy stan układu jest opisany za pomocą współrzędnych położenia i prędkości, to trajektorie w przestrzeni fazowej spełniają twierdzenie Liouville’a, mówiące że objętość dowolnego regionu przestrzeni nie zmienia się w trakcie jego ewolucji (o ile nie następują straty energii).
W termodynamice i mechanice statystycznej opisywanie położenia i prędkości każdej cząstki jest niewykonalne, dlatego używa się przestrzeni definiowanej przez makroskopowe parametry układu, takie jak ciśnienie i temperatura. Punkt takiej przestrzeni określa się jako makrostan.
Przestrzeń fazowa w fizyce kwantowej
W fizyce kwantowej w ujęciu kopenhaskim nie przypisuje się układom fizycznym żadnych trajektorii, co prowadzi do paradoksu pomiaru.
W teorii fali pilotującej de Broglie'a – Bohma układom kwantowym przypisuje się trajektorie deterministyczne: trajektorie te różnią się od trajektorii przewidywanych przez fizykę klasyczną wtedy, gdy pojawiają się efekty kwantowe, takie jak interferencja.
Zobacz też
- płaszczyzna fazowa
- przestrzeń konfiguracyjna
- układ dynamiczny
- dynamika molekularna
- wiązka kostyczna
- rozmaitość symplektyczna
- chaos deterministyczny
- atraktor
- układ Lorentza
Bibliografia
- G. Białkowski, Mechanika klasyczna, Warszawa: PWN, 1975, str. 429-487.
- Wojciech Królikowski, Wojciech Rubinowicz, Mechanika teoretyczna, PWN, Warszawa 2012.
- F. Reif, Fizyka statystyczna, Warszawa: PWN, 1973.
Media użyte na tej stronie
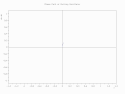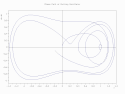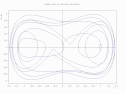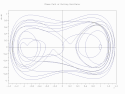
Dwuwymiarowa przestrzeń stanów układu poruszającego się w jednym wymiarze. Na osi pionowej jest prędkość układu, na osi poziomej jego położenie. Układ zaczyna ruch od położenia x=0,71 i prędkości v=0,02. Trajektoria ma postać rozbieżnej spirali.
Autor: Pasimi, Licencja: CC BY-SA 4.0
Phase path of Duffing oscillator plotted as comet plot - plot done with D_2D & D_3D [1]