Przestrzeń jednospójna

(c) Salix alba z angielskiej Wikipedii, CC BY 2.5

Sfera jest jednospójna, gdyż każda pętla może być ściągnieta do punktu tak, że podczas ściągania pętla jest stale zawarta w sferze.

Torus jest spójny, ale nie jest jednospójny, gdyż żadna z kolorowych pętli nie może być ściągnięta do punktu.

Przestrzeń jednospójna – łukowo spójna przestrzeń topologiczna o trywialnej grupie podstawowej.

Innymi słowy jest to przestrzeń topologiczna ${\displaystyle X}$ spełniająca następujące warunkiː

1. dowolne dwa punkty można połączyć drogą (${\displaystyle X}$ jest łukowo spójna),
2. dowolną taką krzywą można przekształcić w sposób ciągły, używając tylko punktów należących do tego obiektu, w dowolną inną krzywą łączącą te punkty (każde dwie drogi łączące ${\displaystyle x\in X}$ oraz ${\displaystyle y\in X}$ są homotopijne).

Zbiór jednospójny – to zbiór ze strukturą topologiczną, który potraktowany jako przestrzeń topologiczna jest przestrzenią jednospójną.

Twierdzenia

Tw. 1 Przestrzeń topologiczna jest jednospójna wtedy i tylko wtedy, gdy jest łukowo spójna i każdą zawartą w niej pętlę da się ściągnąć do punktu, przy czym podczas ściągania pętla musi być zawarta w przestrzeni.

Tw. 2 Przestrzeń topologiczna jest jednospójna wtedy i tylko wtedy, gdy jest łukowo spójna i posiada genus zero (tzn. nie ma otworów).

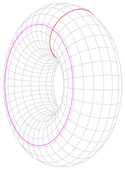
Zbiory z otworem lub otworami (np. torus, okrąg) nie są jednospójne właśnie ze względu na te otwory, które sprawiają, że np. równoleżnika w torusie nie można w sposób ciągły zmniejszyć do punktu^[1].

Przykłady

Przestrzeń niejednospójna, ponieważ pętli okrążających dziury nie da się ściągnąć do punktu.

Obiekty jednospójne:

• W przestrzeni euklidesowej: odcinek, prosta, koło, kula, sfera n-wymiarowa Sⁿ dla n ≥ 2 (np. sfera w przestrzeni trójwymiarowej).
• Przestrzeń Euklidesowa Rⁿ.
• Gdy n > 2, to Rⁿ bez dowolnej liczby punktów, np. bez punktu (0,0).
• Każdy podzbiór wypukły zawarty w Rⁿ.
• Każda przestrzeń wektorowa, w tym przestrzenie Banacha i Hilberta.
• Specjalna grupa unitarna SU(n).

Wszystkie przestrzenie ściągalne są jednospójne (ponieważ każde dwa przekształcenia w przestrzeń ściągalną są homotopijne), jednak nie odwrotnie - na przykład sfera dwuwymiarowa jest jednospójna, ale nie jest ściągalna.

Obiekty niejednospójne:

• Okrąg, torus, butelka Kleina, walec eliptyczny, wstęga Möbiusa.
• Przestrzeń Euklidesowa R² bez np. punktu (0,0).
• Dla n ≥ 2, specjalna grupa ortogonalna SO(n,R).

Przypisy

Bibliografia

• Fritz Reinhardt, Heinrich Soeder: Atlas matematyki. Warszawa: Prószyński i S-ka, s. 243. ISBN 83-7469-189-1.
• Jerzy Mioduszewski: Wykłady z topologii – Topologia przestrzeni euklidesowych. Katowice: Wydawnictwo Uniwersytetu Śląskiego, 1994, s. 170. ISSN 0239-6432.

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Simply Connected, [w:] MathWorld [online], Wolfram Research  (ang.). [dostęp 2022-10-09].