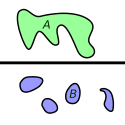
Przestrzeń spójna

Spójne i niespójne podprzestrzenie płaszczyzny euklidesowej: przestrzeń A na górze jest spójna; zacieniowania przestrzeń B na dole nie jest.

Przestrzeń spójna – przestrzeń topologiczna, której nie można rozłożyć na sumę dwóch niepustych, rozłącznych podzbiorów otwartych. Istnieje silniejsze pojęcie przestrzeni spójnej drogowo, w której dowolne dwa punkty dają się połączyć drogą.

Podzbiór przestrzeni topologicznej nazywa się spójnym, jeżeli jest spójny jako podprzestrzeń tej przestrzeni.

Definicja formalna

Niepustą przestrzeń topologiczną ${\displaystyle X}$ nazywa się niespójną, jeżeli jest sumą dwóch niepustych, rozłącznych zbiorów otwartych. W przeciwnym przypadku ${\displaystyle X}$ jest spójna. Podzbiór przestrzeni topologicznej jest spójny, jeśli jest spójny w topologii podprzestrzeni. Dla przestrzeni topologicznej ${\displaystyle X}$ następujące warunki są równoważne:

• ${\displaystyle X}$ jest spójna,
• ${\displaystyle X}$ nie może być rozłożona na dwa rozłączne i niepuste zbiory domknięte^[1],
• jedynymi podzbiorami ${\displaystyle X}$ zarazem otwartymi i domkniętymi (tzw. zbiory otwarto-domknięte) są ${\displaystyle X}$ i zbiór pusty,
• ${\displaystyle X}$ nie daje się przedstawić jako suma dwóch niepustych zbiorów oddzielonych,
• jedynymi funkcjami ciągłymi z ${\displaystyle X}$ w ${\displaystyle \{0,1\}}$ są funkcje stałe.

Spójne składowe

Maksymalne podzbiory spójne dowolnej przestrzeni topologicznej nazywa się spójnymi składowymi lub składowymi spójności tej przestrzeni. Innymi słowy składową zbioru nazywa się taki jego podzbiór spójny, który nie zawiera się w żadnym większym podzbiorze spójnym tego zbioru. Składowe stanowią rozbicie przestrzeni (tzn. są one rozłączne i sumują się do całej przestrzeni). Spójne składowe zbiorów jednopunktowych nazywa się często spójnymi składowymi punktu należącego do takiego zbioru. Każda składowa jest domkniętym podzbiorem oryginalnej przestrzeni. W ogólności składowe nie muszą być otwarte: przykładowo składowymi liczb wymiernych są zbiory jednopunktowe. Jednakże składowe zbiorów otwartych płaszczyzny są otwarte.

Niech ${\displaystyle \Gamma _{x}}$ będzie spójną składową punktu ${\displaystyle x}$ przestrzeni topologicznej ${\displaystyle X,}$ zaś ${\displaystyle \Gamma _{x}'}$ oznacza przekrój wszystkich zbiorów otwarto-domkniętych zawierających ${\displaystyle x}$ (nazywa się go quasi-składową tego punktu). Wówczas ${\displaystyle \Gamma _{x}\subseteq \Gamma '_{x}.}$ Równość zachodzi, jeżeli ${\displaystyle X}$ jest zwartą przestrzenią Hausdorffa bądź jest lokalnie spójna.

Niespójność

(1) Przestrzeń, której wszystkie składowe są zbiorami jednopunktowymi, nazywa się całkowicie niespójną.

Np. przestrzeniami całkowicie niespójnymi są: zbiór liczb naturalnych oraz zbiór liczb wymiernych z naturalną topologią metryczną daną jako wartość bezwzględna różnicy dwóch liczb.

(2) Z całkowitą niespójnością związana jest inna własność - całkowite oddzielenie:

Df. Przestrzeń ${\displaystyle X}$ nazywa się całkowicie oddzieloną, jeżeli dla każdych dwóch elementów ${\displaystyle x,y\in X}$ istnieją rozłączne otoczenia ${\displaystyle U}$ punktu ${\displaystyle x}$ oraz ${\displaystyle V}$ punktu ${\displaystyle y}$ takie, że ${\displaystyle X}$ jest sumą mnogościową ${\displaystyle U}$ oraz ${\displaystyle V}$

Tw. 1 Każda przestrzeń całkowicie oddzielona jest całkowicie niespójna; jednak wynikanie w drugą stronę nie zachodzi. Niech dane będą przykładowo dwa egzemplarze liczb wymiernych ${\displaystyle \mathbb {Q} }$ utożsamione ze sobą w każdym punkcie poza zerem. Otrzymana przestrzeń, z topologią ilorazową, jest całkowicie niespójna. Rozważając jednak dwa egzemplarze zera widać, że przestrzeń nie jest całkowicie oddzielona. Istotnie, nie jest ona nawet Hausdorffa, a warunek całkowitego oddzielenia jest ściśle mocniejszy niż warunek hausdorffowości przestrzeni.

Twierdzenia

Tw. 2 Ciągłe przekształcenia zachowują spójność przestrzeni.

Np. Ciągła funkcja zmiennej rzeczywistej w liczby rzeczywiste odwzorowuje przedział liczbowy w inny przedział.

Twierdzenie to jest równoważne twierdzeniu o wartości pośrednie (tzw. własności Darboux):

Tw. 3 Jeżeli ciągła funkcja rzeczywista przyjmuje jako wartości liczby ${\displaystyle a,b,}$ to przyjmuje także wartość ${\displaystyle c}$ leżącą między nimi.

Tw. 3 Każda ciągła funkcja rzeczywista na przestrzeni spójnej ma własność Darboux.

Tw. 4 Suma dwóch zbiorów spójnych o niepustym przekroju jest zbiorem spójnym.

Tw. 5 Iloczyn kartezjański dowolnej rodziny przestrzeni spójnych jest spójny.

Spójność drogowa i łukowa

Drogowo spójny podzbiór płaszczyzny.

Niech dana będzie przestrzeń topologiczna ${\displaystyle (X,\tau ).}$ Przestrzeń ${\displaystyle X}$ nazywa się drogowo spójną (0-spójną), jeżeli dwa dowolne jej punkty można połączyć drogą, tzn. dla każdych dwóch punktów ${\displaystyle x,y}$ istnieje funkcja ciągła ${\displaystyle f_{x,y}\colon [0,1]\to X}$ taka, że ${\displaystyle f_{x,y}(0)=x}$ oraz ${\displaystyle f_{x,y}(1)=y.}$

Przestrzeń ${\displaystyle X}$ nazywa się łukowo spójną, jeżeli dwa dowolne jej punkty można połączyć łukiem^[2], tzn. istnieje droga ${\displaystyle f}$ będąca homeomorfizmem przedziału jednostkowego ${\displaystyle [0,1]}$ oraz jego obrazu ${\displaystyle f\left([0,1]\right).}$

Zachodzą następujące związki między różnymi rodzajami spójności:

łukowa spójność ${\displaystyle \Rightarrow }$ drogowa spójność ${\displaystyle \Rightarrow }$ spójność;

Przykładem pokazującym, że nie można odwrócić pierwszego wynikania jest przestrzeń Sierpińskiego, a drugiego – sinusoida zagęszczona. Mimo wszystko, jeżeli rozpatrywana przestrzeń jest Hausdorffa, to pojęcia drogowej i łukowej spójności pokrywają się. Podobnie dla otwartych podzbiorów przestrzeni euklidesowej pokrywają się pojęcia łukowej spójności i spójności.

Spójność lokalna

Przestrzeń topologiczną nazywa się lokalnie spójną w punkcie, jeżeli każde otoczenie tego punktu zawiera otwarte otoczenie spójne. Jest ona lokalnie spójna, gdy ma bazę składającą się ze zbiorów spójnych. Można pokazać, że przestrzeń jest lokalnie spójna wtedy i tylko wtedy, gdy każda składowa dowolnego zbioru otwartego tej przestrzeni jest otwarta. Przykładem przestrzeni spójnej, która nie jest lokalnie spójna jest sinusoida zagęszczona.

Podobnie o przestrzeni topologicznej mówi się, że jest lokalnie drogowo spójna, jeżeli jej bazę stanowią zbiory drogowo spójne. Otwarty podzbiór przestrzeni lokalnie drogowo spójnej jest spójny wtedy i tylko wtedy, gdy jest drogowo spójny. Uogólnia to wcześniejsze stwierdzenie o ${\displaystyle \mathbb {R} ^{n}}$ oraz ${\displaystyle \mathbb {C} ^{n},}$ które obie są lokalnie drogowo spójne. Ogólniej: dowolna rozmaitość topologiczna jest lokalnie drogowo spójna.

Dla przestrzeni lokalnie spójnej (np. płaszczyzny) rozbicie podzbiorów otwartych na składowe jest identyczne z rozbiciem na obszary.

Continuum

Continuum to spójna przestrzeń zwarta^[3]. Przykładami continuów są: odcinek domknięty, koło, okrąg, kwadrat, sześcian (wszystkie z brzegiem) oraz pseudołuk.

Ponieważ przekształcenia ciągłe zachowują zwartość, jak i spójność, więc obrazem continuum przez dowolną funkcję ciągłą jest continuum.

Każde continuum będące przestrzenią metryczną lokalnie łukowo spójną jest obrazem odcinka ${\displaystyle [0,1]}$ w pewnej funkcji ciągłej. Wynika stąd, że istnieje funkcja ciągła z odcinka ${\displaystyle [0,1],}$ której obrazem jest dowolny kwadrat na płaszczyźnie (wraz z brzegiem); funkcję taką można skonstruować nie korzystając z tego twierdzenia – zob. krzywa Peana.

Przykłady

Każda przestrzeń, zatem także przestrzenie liczb rzeczywistych ${\displaystyle \mathbb {R} ,}$ zespolonych ${\displaystyle \mathbb {C} ,}$ czy przestrzeń euklidesowa ${\displaystyle \mathbb {R} ^{n}}$ dowolnego wymiaru ${\displaystyle n,}$ jest spójna. Każdy przedział liczbowy jest przestrzenią spójną. Torus oraz sfera są zbiorami spójnymi.

Przestrzeń otrzymana z usunięcia prostej z płaszczyzny nie jest spójna. Niespójne są również płaszczyzna z usuniętym pierścieniem kołowym, czy suma dwóch rozłącznych kół dwuwymiarowej przestrzeni euklidesowej.

Zobacz też

• przestrzeń jednospójna i wielospójna

Przypisy

Bibliografia

• Jerzy Mioduszewski: Wykłady z topologii. Topologia przestrzeni euklidesowych. Katowice: Wydawnictwo Uniwersytetu Śląskiego, 1994. ISSN 0239-6432.

Linki zewnętrzne

• AgnieszkaA. Bojanowska AgnieszkaA., Przestrzeń spójna, [w:] pismo „Delta” [online], deltami.edu.pl, kwiecień 2019, ISSN 0137-3005 [dostęp 2022-07-19]  (pol.).
• Eric W.E.W. Weisstein Eric W.E.W., Connected Set, [w:] MathWorld [online], Wolfram Research  (ang.). [dostęp 2022-10-09].