Punkt przegięcia

Niektóre z zamieszczonych tu informacji wymagają weryfikacji. Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tego artykułu. Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tego artykułu.

Przykładowy wykres funkcji zawierającej punkt przegięcia (w); styczna w tym punkcie została zaznaczona na czerwono.

Punkt przegięcia – niejednoznaczne pojęcie matematyczne, definiowane inaczej – i nierównoważnie – w analizie oraz geometrii. W obu dyscyplinach występują różne konwencje znaczeń:

• dla funkcji rzeczywistej o zmiennej rzeczywistej jest to pewien punkt w jej dziedzinie lub na wykresie. Zachodzi w nim zmiana wypukłości, tj. po jednej stronie przegięcia funkcja jest wypukła, a po drugiej – wklęsła^[1][2]. Ta definicja jest niejednoznaczna przez różne użycie nazw „wypukłość” i „wklęsłość”; oprócz tego bywa zawężana dodatkowymi warunkami na zachowanie funkcji w tym miejscu. Przy niektórych z tych zawężeń – oraz innych definicjach, nieodwołujących się do wypukłości – punkt przegięcia wykresu staje się szczególnym przypadkiem sensu geometrycznego:
• dla ogólnych krzywych płaskich punkt przegięcia to taki, w którym istnieje styczna i „przechodzi” ona z jednej strony krzywej na drugą^[3][4]. W sensie ścisłym i węższym^[5]: w pewnym sąsiedztwie przegięcia krzywa zawiera się we wnętrzu kątów wierzchołkowych utworzonych przez styczną i normalną^[6]. Można to też formalizować przez zmianę znaku krzywizny^[7], choć wymaga to innych założeń o własnościach krzywej.

Oprócz tego znaczenia z pierwszej grupy mają swoje warunki wystarczające jak:

• ekstremum pierwszej pochodnej we wnętrzu dziedziny^[8],
• zmiana znaku drugiej pochodnej^[9][10],
• zmiana znaku pewnych wyrażeń z pierwszą lub drugą pochodną w przegięciu,
• zerowanie się pochodnych kolejnych rzędów między pierwszym a pewnym rzędem nieparzystym, dla którego wartość pochodnej jest niezerowa^[11][12]:

${\displaystyle \mathop {\exists } \limits _{k\in \mathbb {N} _{+}}{\Big (}f^{(2k+1)}(x_{0})\neq 0\wedge \mathop {\forall } \limits _{n\in \mathbb {N} }1<n<2k+1\Rightarrow f^{(n)}(x_{0})=0{\Big )}.}$

Kryteria te istnieją dzięki twierdzeniom o różniczkowalnych funkcjach wypukłych i wklęsłych. Przy pewnym zawężeniu pojęć te warunki wystarczające stają się równoważnymi; bywają wręcz używane jako definicje^[11].

Pojęcie to wprowadził do matematyki prawdopodobnie Gilles de Roberval; posłużył się nim w 1636 roku, w liście do Pierre’a Fermata. O przegięciach pod innymi nazwami wspominali potem między innymi Gottfried Wilhelm Leibniz i Isaac Newton^[13].

Przegięcia funkcji rzeczywistych

Wykres funkcji trzeciego stopnia ${\displaystyle y\!=\!x^{3}}$ (sześcianu), czasem nazywany parabolą sześcienną. Punktem przegięcia jest tu początek układu współrzędnych^[14] (0,0), z obu perspektyw^[a]: 1) dla argumentów ujemnych ${\displaystyle (x\!<\!0)}$ funkcja jest ściśle wklęsła, a dla dodatnich ${\displaystyle (x\!>\!0)}$ – ściśle wypukła; 2) styczną jest tu oś pozioma (Ox), normalną – oś pionowa (Oy), a cały wykres znajduje się w przeciwległych ćwiartkach układu (pierwszej i trzeciej).

Tangensoida – wykres funkcji tangens ${\displaystyle y\!=\!\operatorname {tg} x.}$ Jej miejsca zerowe to wielokrotności 90° lub pi ${\displaystyle (\pi )}$ radianów: ${\displaystyle x\!=\!k\pi .}$ Punkty te są zarazem przegięciami^[2]; prostych stycznych ani normalnych tu nie przedstawiono.

Wykres pierwiastka sześciennego ${\displaystyle y\!=\!{\sqrt[{3}]{x}}.}$ To przykład funkcji, która ma punkt przegięcia ${\displaystyle (x_{0}\!=\!0),}$ ale druga pochodna ${\displaystyle (y'')}$ się w nim nie zeruje i w dodatku nie istnieje. W tym miejscu nie ma nawet właściwej pierwszej pochodnej; dąży tam ona do nieskończoności: ${\displaystyle y'\!\rightarrow \!+\infty }$ przy ${\displaystyle x\!\rightarrow \!0.}$

Wykres funkcji wymiernej ${\displaystyle y=1/x}$ – przykład hiperboli. Początek układu współrzędnych (0,0) rozdziela tu przedział ścisłej wklęsłości ${\displaystyle (x\!<\!0)}$ od przedziału ścisłej wypukłości ${\displaystyle (x\!>\!0).}$ Mimo to punkt ${\displaystyle x\!=\!0}$ zwykle nie jest uznawany za przegięcie – jako liczba spoza dziedziny tej funkcji^[14].

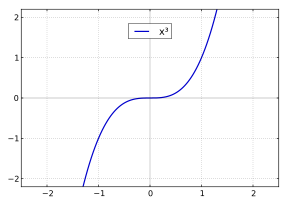
Szeroka definicja przez wypukłość

Niech ${\displaystyle f}$ będzie funkcją zmiennej rzeczywistej o wartościach rzeczywistych: ${\displaystyle f\colon X\to Y,}$ gdzie ${\displaystyle X,Y\subseteq \mathbb {R} .}$ Wtedy mówi się, że ${\displaystyle f}$ ma punkt przegięcia w ${\displaystyle x=x_{0}}$ wtedy i tylko wtedy, gdy w pewnym otoczeniu punktu ${\displaystyle x_{0}}$ jest po jednej z jego stron ściśle wypukła, a po drugiej – ściśle wklęsła^[14]. Formalnie oznacza to, że istnieje liczba ${\displaystyle r\in \mathbb {R} _{+},}$ dla której funkcja ${\displaystyle f{:}}$

a) jest ściśle wklęsła na przedziale ${\displaystyle (x_{0}-r,x_{0})}$ i ściśle wypukła na przedziale ${\displaystyle (x_{0},x_{0}+r);}$

b) odwrotnie – jest ona ściśle wypukła na ${\displaystyle (x_{0}-r,x_{0})}$ i ściśle wklęsła na ${\displaystyle (x_{0},x_{0}+r).}$

Wypukłość i wklęsłość są definiowane różnie – i nierównoważnie – przez różnych autorów. W ogólności funkcja ${\displaystyle f{:}}$

• jest ściśle wklęsła na przedziale ${\displaystyle [u,v]\subseteq X}$ wtedy i tylko wtedy, gdy jest ciągła na przedziale ${\displaystyle (u,v)}$ i:

${\displaystyle \forall {u\leqslant a<b<c\leqslant v}:{\frac {f(b)-f(a)}{b-a}}>{\frac {f(c)-f(b)}{c-b}}}$

lub (równoważna definicja):

${\displaystyle \forall {u\leqslant a<b\leqslant v}:f\left({\frac {a+b}{2}}\right)>{\frac {f(a)+f(b)}{2}}.}$

• Podobnie funkcja jest ściśle wypukła na tym przedziale wtedy i tylko wtedy, gdy jest ciągła na tym przedziale i:

${\displaystyle \forall {u\leqslant a<b<c\leqslant v}:{\frac {f(b)-f(a)}{b-a}}<{\frac {f(c)-f(b)}{c-b}}}$

lub (równoważna definicja):

${\displaystyle \forall {u\leqslant a<b\leqslant v}:f\left({\frac {a+b}{2}}\right)<{\frac {f(a)+f(b)}{2}}.}$

Inne definicje

Wśród funkcji nieróżniczkowalnych istnieją takie, które w punkcie nieróżniczkowalności mają styczną pionową (tu ${\displaystyle x\!=\!0).}$ Takie funkcje mogą ją przecinać, nie zmieniając przy tym wypukłości – przez co punkty te nie są zaliczane do przegięć^[5]. Wykresy takich funkcji nie spełniają też ścisłej geometrycznej definicji przegięcia, opartej na kątach wierzchołkowych między styczną a normalną.

Niektórzy matematycy definiują punkty przegięcia funkcji przez wypukłość i wklęsłość w sąsiedztwie, ale określone inaczej – za pomocą stycznych^[1][15]. Wymaga to wzmocnienia założenia ciągłości o różniczkowalność^[16]. Zdarza się też dodatkowy wymóg, by w tym sąsiedztwie przegięcia istniała także druga pochodna i to ciągła^[17]; takie funkcje bywają nazywane klasą ${\displaystyle {\mathcal {C}}^{2}}$.

Nierzadko zakłada się też dodatkowe własności funkcji ${\displaystyle f}$ w samym punkcie ${\displaystyle x_{0}}$ jak:

• określoność w tym punkcie^[14] (przyjmowanie w nim jakiejś wartości: ${\displaystyle x_{0}\in X}$);
• ciągłość^[b]: ${\displaystyle f\in {\mathcal {C}};}$
• istnienie w nim pochodnych jednostronnych ${\displaystyle (f'_{\pm })}$ spełniających pewne nierówności^[2];
• istnienie w nim stycznej^[18], czyli spełnianie jednego z dwóch warunków^[19]:
  • istnienie pochodnej właściwej lub niewłaściwej (tj. nieskończonej)^[20]: ${\displaystyle f'(x_{0})\in {\overline {\mathbb {R} }};}$
  • istnienie jednostronnych pochodnych niewłaściwych: ${\displaystyle f'_{+}(x_{0}),f'_{-}(x_{0})\in \{\pm \infty \};}$
• różniczkowalność^[16] – istnienie pochodnej właściwej (tj. skończonej): ${\displaystyle f'(x_{0})\in \mathbb {R} ;}$
• istnienie drugiej pochodnej (podwójna różniczkowalność) i jej ciągłość^[17][21]: ${\displaystyle f\in {\mathcal {C}}^{2}.}$

Czasem przegięcie funkcji jest definiowane bez wypukłości ani wklęsłości. Niektórzy odwołują się do własności związanych ze styczną w tym punkcie ${\displaystyle (x_{0}){:}}$

• nieformalnie przegięcie to punkt przecinania stycznej^[21]. To znaczenie obejmuje też funkcje bez zmiany wypukłości, w dodatku z wykresem po jednej stronie prostej normalnej – wbrew ogólnej definicji przegięcia krzywej płaskiej. Tak się może dziać w wypadku stycznych pionowych^[5].
• Wykluczenie stycznych pionowych oznacza, że w przegięciu istnieje pochodna skończona ${\displaystyle (f'(x_{0})\in \mathbb {R} ).}$ Wtedy przebijanie stycznej to formalnie zmiana znaku funkcji ${\displaystyle f-s,}$ gdzie ${\displaystyle s(x)=f(x_{0})+f'(x_{0})(x-x_{0})}$ to funkcja opisująca styczną w punkcie ${\displaystyle x_{0}}$^[c][20]. Ta definicja również bywa zawężana^[d]. Wszystkie takie przegięcia są zgodne z definicją geometryczną (dla ogólnej krzywej płaskiej); mimo to mogą one nie zmieniać wypukłości funkcji, co opisano dalej.

Zdarza się jeszcze inna definicja – pozwalająca rozstrzygnąć, czy punkt jest przegięciem, za pomocą samych pochodnych w tym punkcie. Wymaga to co najmniej trzykrotnej różniczkowalności (istnienia ${\displaystyle f'''(x_{0})}$)^[11].

Przykłady nierównoważności

Powyższe definicje nie są sobie równoważne – istnieją funkcje z punktami spełniającymi tylko niektóre z nich. Są przypadki zmiany wypukłości, w których:

• druga pochodna jest nieciągła;
• nie ma drugiej pochodnej – por. funkcja ${\displaystyle u(x):=x|x|.}$ W punkcie ${\displaystyle x=0}$ istnieje przegięcie, bo pierwsza pochodna ${\displaystyle u'(x)=2|x|}$ ma tam swoje minimum. Mimo to drugie pochodne jednostronne są tam różne ${\displaystyle (u''_{-}\neq u''_{+}),}$ więc obustronna druga pochodna nie istnieje;
• nie ma pierwszej pochodnej właściwej (skończonej) – por. pierwiastek kubiczny (sześcienny);
• nie ma nawet niewłaściwej pierwszej pochodnej;
• nie ma stycznej^[22];
• nie ma ciągłości;
• nie ma wartości w tym punkcie; por. ${\displaystyle v(x):=1/x.}$

Istnieją też funkcje z punktami spełniającymi „geometryczną” definicję przegięcia (przez styczną), ale bez zmiany wypukłości w tym punkcie^[20][2]:

${\displaystyle g(x):={\begin{cases}-x^{2}(2+\sin {\frac {1}{x}})&{\text{dla }}x<0,\\0&{\text{dla }}x=0,\\x^{2}(2+\sin {\frac {1}{x}})&{\text{dla }}x>0.\end{cases}}}$

Ta funkcja jest różniczkowalna w zerze ${\displaystyle (g'(0)=0),}$ ale jej pochodna jest tam nieciągła i nawet nie ma granic jednostronnych^[23]. Warunek ciągłości pochodnej ${\displaystyle (f\in {\mathcal {C}}^{1})}$ nie usuwa jednak takich przypadków. Nie robi tego nawet postulat dwukrotnej różniczkowalności z ciągłą drugą pochodną ${\displaystyle (f\in {\mathcal {C}}^{2}).}$ Istnieją funkcje tej klasy, które również przecinają swoją styczną bez zmiany wypukłości w tym punkcie^[24]:

${\displaystyle k(x):={\begin{cases}x^{5}(1+\sin ^{2}{\frac {1}{x}})&{\text{dla }}x\neq 0,\\0&{\text{dla }}x=0.\end{cases}}}$

Warunki konieczne i wystarczające

Wykres czwartej potęgi: ${\displaystyle y\!=\!x^{4}.}$ To przykład funkcji, która w pewnym punkcie ${\displaystyle (x\!=\!0)}$ ma zerową drugą pochodną, ale nie ma tam przegięcia^[21]. Druga pochodna ${\displaystyle (y''\!=\!12x^{2})}$ nie zmienia tam znaku – po obu stronach jest dodatnia – a pierwsza pochodna ${\displaystyle (y'\!=\!4x^{3})}$ nie ma tam ekstremum. Czwarta potęga jest ściśle wypukła w całej dziedzinie^[2], a w zerze ma minimum.

Wykres wielomianu czwartego stopnia: ${\displaystyle y=x^{4}\!-\!x.}$ To przykład funkcji, której druga pochodna ${\displaystyle (y''\!=\!12x^{2})}$ zeruje się w punkcie niebędącym ani przegięciem, ani ekstremum.

W przegięciach druga pochodna w ogólności nie musi istnieć, ale może przyjmować tylko zerową wartość ${\displaystyle (f''(x_{0})=0)}$^[3][4]. Ten warunek konieczny nie jest jednak warunkiem wystarczającym:

• jeśli obie pochodne (pierwsza i druga) się zerują, to punkt może nie być przegięciem, lecz ekstremum^[25] – por. ${\displaystyle y=x^{4};}$
• jeśli druga pochodna się zeruje, a pierwsza nie, to punkt nie jest ekstremum, ale nie musi też być przegięciem; por. jedna z dalszych ilustracji.

Dla różnych klas funkcji można wskazać różne warunki wystarczające przegięcia:

• Jeśli funkcja ma obustronną pochodną w pewnym otoczeniu punktu ${\displaystyle x_{0},}$ wówczas warunkiem wystarczającym jest właściwe ekstremum lokalne pierwszej pochodnej w punkcie ${\displaystyle x_{0}.}$ Ten warunek nie jest w ogólności konieczny – w sąsiedztwie przegięcia pochodna może w ogóle nie istnieć^[26]. Mimo to, tak jak napisano wyżej, czasem zakłada się różniczkowalność badanej funkcji w całym przedziale – wprost lub przez definiowanie wypukłości za pomocą stycznych.
• Warunkiem wystarczającym istnienia punktu przegięcia jest też istnienie drugiej pochodnej funkcji równej zeru w punkcie ${\displaystyle x_{0}}$ oraz zmiana jej znaku w tym punkcie^[4].
• Dla funkcji trzykrotnie różniczkowalnej warunkiem wystarczającym jest: ${\displaystyle f''(x_{0})=0\wedge f'''(x_{0})\neq 0.}$ W ogólności: jeśli w jakimś punkcie pierwsza nieznikająca (różna od zera) pochodna jest rzędu nieparzystego większego niż dwa, to jest tam przegięcie^[27].

Rola przegięć

Poszukiwanie przegięć to jeden z klasycznych elementów badania przebiegu zmienności funkcji rzeczywistych^[14] ${\displaystyle (f\colon X\rightarrow \mathbb {R} ,X\subseteq \mathbb {R} ).}$ Punkty te mogą się pojawić w analizie pochodnych, począwszy od pierwszej – mogą się znaleźć wśród punktów krytycznych badanej funkcji ${\displaystyle (f).}$ Przegięcia – tak jak lokalne ekstrema – mogą występować zarówno wśród:

• punktów nieróżniczkowalności (braku pochodnej)^[14]; przy czym taki punkt może być jednocześnie i ekstremum, i przegięciem^[22];
• punktów stacjonarnych, czyli miejsc zerowych pierwszej pochodnej ${\displaystyle (f'(x_{s})=0).}$ Takie punkty stacjonarne bez ekstremum w przypadku jednowymiarowym mogą należeć do przegięć. Bywają nazywane punktami siodłowymi^[28], przy czym te ostatnie są też definiowane inaczej – geometrycznie, jako punkty zerowej krzywizny^[29]. Wtedy punkty siodłowe nie są szczególnym przypadkiem różniczkowalnych przegięć, lecz ich uogólnieniem na wiele wymiarów.

W ogólności przegięcie wykresu nie ma ścisłego związku z pierwszą pochodną. Jeśli w takich punktach ona istnieje, to może mieć dowolny znak i być nieskończona (niewłaściwa), co ilustrują wykresy obok. Przegięcia są bliżej związane z dalszymi pochodnymi – przez różne warunki konieczne lub wystarczające, opisane wyżej.

Przegięcia wielomianów

Wielomian n-tego stopnia ${\displaystyle (n\geqslant 2)}$ ma co najwyżej ${\displaystyle n-2}$ punktów przegięcia. Wynika to z połączenia trzech faktów:

• podwójna różniczkowalność wielomianów, dająca też ciągłą drugą pochodną (klasa ${\displaystyle {\mathcal {C}}^{2}}$); przegięcia takich funkcji muszą spełniać warunek konieczny, jakim jest zerowanie się drugiej pochodnej ${\displaystyle (f''(x_{0})=0);}$
• wzór na pochodną wielomianu – dla ${\displaystyle n\geqslant 1}$ pochodna zmniejsza stopień wielomianu o jeden. Przez to druga pochodna ma stopień niższy o dwa ${\displaystyle (\deg f''=\deg f-2);}$
• zasadnicze twierdzenie algebry mówi między innymi, że liczba pierwiastków rzeczywistych wielomianu rzeczywistego nie przekracza jego stopnia; tutaj liczba pierwiastków drugiej pochodnej nie przekracza ${\displaystyle n-2.}$

W szczególności funkcje kwadratowe – dla których ${\displaystyle n=2}$ – nie mają przegięć. Dotyczy to także wielomianów stopnia niższego niż dwa, czasem zwanych funkcjami liniowymi.

Uogólnienie na inne krzywe płaskie

Pojęcie punktu przegięcia może też zostać uogólnione na krzywe płaskie niebędące wykresami funkcji, zwłaszcza na krzywe z punktami regularnymi, tj. o unikalnej stycznej. Tak jak wspomniano, tutaj również występują różne konwencje:

• nieformalnie – w punkcie przegięcia krzywa przechodzi z jednej strony stycznej na drugą^[30];

• w sensie ścisłym i węższym^[5]: w pewnym sąsiedztwie przegięcia krzywa zawiera się we wnętrzu kątów wierzchołkowych utworzonych przez styczną i normalną^[6];

• inna ścisła definicja mówi o rozdzielaniu punktów o krzywiźnie dodatniej i ujemnej^[7], co wymaga zerowania się krzywizny w tym punkcie^[31]. Tak rozumiane przegięcie jest szczególnym, jednowymiarowym przypadkiem punktu siodłowego lub – przy innych definicjach – jego odpowiednikiem.

W miarę zbliżania się do punktu przegięcia promień krzywizny wykresu funkcji dwukrotnie różniczkowalnej rośnie do nieskończoności. Mówi się skrótowo, że jest on w punkcie przegięcia nieskończony. Oznacza to, że w otoczeniu punktu przegięcia krzywa (w szczególności np. wykres funkcji) jest lepiej przybliżana linią prostą niż łukiem okręgu.

Zobacz też

• funkcja monotoniczna

Uwagi

Przypisy

Bibliografia

Książki publikowane drukiem

• Stefan Banach: Rachunek różniczkowy i całkowy. Wyd. VI. Warszawa: Państwowe Wydawnictwo Naukowe, 1957.
• G.M. Fichtenholz: Rachunek różniczkowy i całkowy. Wyd. 12. T. 1. Warszawa: Wydawnictwo Naukowe PWN, 1999. ISBN 83-01-02175-6.
• Jerzy Królikowski, Celestyn Steckiewicz: Matematyka. Wzory, definicje i tablice. Wyd. VIII poprawione. Warszawa: Wydawnictwa Komunikacji i Łączności, 1964.
• Michał Krych: Analiza matematyczna dla ekonomistów. Wyd. I. Warszawa: Wydawnictwa Uniwersytetu Warszawskiego, 2010. ISBN 978-83-235-0776-5.
• Włodzimierz Krysicki, Lech Włodarski: Analiza matematyczna w zadaniach. Wyd. XXI. T. 1. Warszawa: Wydawnictwo Naukowe PWN, 1994. ISBN 83-01-01460-1.
• Włodzimierz Krysicki, Lech Włodarski: Analiza matematyczna w zadaniach. Wyd. 27. T. 2. Warszawa: Wydawnictwo Naukowe PWN, 2006. ISBN 978-83-01-14296-4.
• Franciszek Leja: Rachunek różniczkowy i całkowy ze wstępem do równań różniczkowych. Wyd. VI. Warszawa: Państwowe Wydawnictwo Naukowe, 1963, seria: Biblioteka Matematyczna, tom 2.
• Anna Leksińska, Wacław Leksiński: Elementy matematyki wyższej dla studentów i kandydatów na studia. Warszawa: Państwowe Wydawnictwo Naukowe, 1978, seria: Matematyka dla politechnik.
• Wacław Leksiński, Ireneusz Nabiałek, Wojciech Żakowski: Matematyka. Definicje, twierdzenia, przykłady, zadania. Wyd. V. Warszawa: Wydawnictwa Naukowo-Techniczne, 1995, seria: Podręczniki akademickie: elektronika, informatyka, telekomunikacja. ISBN 83-204-1892-5.
• Jerzy Ryll, Maciej Skwarczyński: Działania nieskończone [w:] Leksykon matematyczny. Warszawa: Wydawnictwo „Wiedza Powszechna”, 1993. ISBN 83-214-0783-8.
• Włodzimierz Wrona: Matematyka. Podstawowy wykład politechniczny, część I. Wyd. II poprawione. Warszawa: Państwowe Wydawnictwo Naukowe, 1965.
• Dariusz Wrzosek: Matematyka dla biologów. Wyd. II, zmienione. Warszawa: Wydawnictwa Uniwersytetu Warszawskiego, 2016. ISBN 978-83-235-0460-3.
• G.I. Zaporożec: Metody rozwiązywania zadań z analizy matematycznej. Piotr Kucharczyk (tłum.). Wyd. I. Warszawa: Wydawnictwa Naukowo-Techniczne, 1967.
• Wojciech Żakowski: punkt przegięcia, [w:] Mały słownik matematyczny. Warszawa: Wydawnictwo „Wiedza Powszechna”, 1972.

Dokumenty cyfrowe

• PawełP. Strzelecki PawełP., Analiza matematyczna I (skrypt wykładu), 14 grudnia 2018 [dostęp 2022-01-27] .

Linki zewnętrzne

• Mariusz Śliwiński, Wklęsłość i wypukłość krzywej, math.edu.pl [dostęp 2022-07-02].