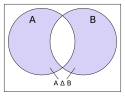
Różnica symetryczna zbiorów

Diagram Venna dla ${\displaystyle A{\dot {-}}B}$ (różnica symetryczna oznaczona jest kolorem jasnofioletowym)

Różnica symetryczna zbiorów ${\displaystyle A}$ i ${\displaystyle B}$ – zbiór, do którego należą elementy zbioru ${\displaystyle A}$ nienależące do zbioru ${\displaystyle B}$ oraz elementy należące do zbioru ${\displaystyle B,}$ ale nienależące do zbioru ${\displaystyle A}$^[1].

Różnicę symetryczną oznaczamy symbolem ${\displaystyle {\dot {-}}}$^[1][2][3]. Używane są również symbole ${\displaystyle \Delta }$ oraz ${\displaystyle \oplus }$^[4].

Definicja formalna

${\displaystyle A{\dot {-}}B=(A\setminus B)\cup (B\setminus A)}$^[1].

Własności

• ${\displaystyle A{\dot {-}}B=(A\cup B)\setminus (A\cap B).}$
• Jeśli ${\displaystyle A\subseteq B,}$ to ${\displaystyle A{\dot {-}}B=B\setminus A.}$
• Za pomocą różnicy symetrycznej i iloczynu można zdefiniować sumę i różnicę zbiorów:
  • Jeśli ${\displaystyle A\cap B=\emptyset ,}$ to ${\displaystyle A{\dot {-}}B=A\cup B;}$ ogólniej, ${\displaystyle A\cup B=A{\dot {-}}B{\dot {-}}(A\cap B)}$^[2].
  • ${\displaystyle A\setminus B=A{\dot {-}}(A\cap B)}$^[2]
• Zbiór ${\displaystyle A{\dot {-}}(B{\dot {-}}C)}$ składa się z elementów należących albo do wszystkich trzech zbiorów, albo do dokładnie jednego z nich. Z uwagi tej wynika łączność tego działania^[3][2].
• Zbiór potęgowy ${\displaystyle {\mathcal {P}}(A)}$ zbioru ${\displaystyle A}$ z operacją różnicy symetrycznej tworzy grupę przemienną, gdyż działanie to:
  • jest operacją łączną
  • jest operacją przemienną
  • ma element neutralny – jest nim zbiór pusty: ${\displaystyle A{\dot {-}}\varnothing =A}$^[3]
  • ma element odwrotny dla dowolnego zbioru ${\displaystyle A}$ – jest nim sam zbiór ${\displaystyle A,}$ gdyż ${\displaystyle A{\dot {-}}A=\varnothing }$^[3].
• Wraz z operacją przekroju powyższa grupa tworzy przemienny, łączny pierścień z jedynką, w którym ${\displaystyle A\cap A=A}$ dla wszystkich ${\displaystyle A\in {\mathcal {P}}(A).}$ W szczególności pierścień ten jest przykładem pierścienia Boole’a.

Różnica symetryczna w logice

Przyjmując, że zdanie logiczne ${\displaystyle a}$ oznacza: „${\displaystyle x}$ należy do zbioru ${\displaystyle A}$”, natomiast zdanie ${\displaystyle b}$: „${\displaystyle x}$ należy do zbioru ${\displaystyle B}$” to zdanie ${\displaystyle x\in A{\dot {-}}B}$ można równoważnie zapisać jako ${\displaystyle a{\underline {\lor }}b,}$ gdzie ${\displaystyle {\underline {\lor }}}$ oznacza alternatywę rozłączną.

Zobacz też

• dopełnienie zbioru
• iloczyn kartezjański
• iloczyn zbiorów
• różnica zbiorów
• suma zbiorów

Przypisy

Bibliografia

• Kazimierz Kuratowski, Andrzej Mostowski: Teoria mnogości. Warszawa: Polskie Towarzystwo Matematyczne, 1952, seria: Monografie matematyczne, t. 27. OCLC 250182901. [dostęp 2016-09-23].
• Kazimierz Kuratowski: Wstęp do teorii mnogości i topologii. Wyd. 8. Warszawa: PWN, 1980, seria: Biblioteka matematyczna, t. 9. ISBN 83-01-01372-9.
• Helena Rasiowa: Wstęp do matematyki współczesnej. Wyd. 5. Warszawa: PWN, 1975, seria: Biblioteka matematyczna, t. 30. OCLC 749626864.
• Kenneth A. Ross, Charles R.B Wright: Matematyka dyskretna. E. Sepko-Guzicka (tłum.), W. Guzicki (tłum.), P. Zakrzewski (tłum.). Warszawa: Wydawnictwo Naukowe PWN, 1996. ISBN 83-01-12129-7.