Równanie Lotki-Volterry

Równanie Lotki-Volterry (model Lotki-Volterry, model drapieżnik-ofiara) – nieliniowy układ równań różniczkowych pierwszego stopnia.
Poniższy model został zaproponowany w 1926 przez Vito Volterrę do opisu populacji ryb odławianych w Morzu Adriatyckim. Niezależnie od Volterry równoważne równania do opisu oscylacji stężeń substancji w hipotetycznej reakcji chemicznej otrzymał Alfred James Lotka w 1920 roku[1].
Równanie Lotki-Voltery stanowi model układów dynamicznych występujących w ekosystemach (np. w symulacji zachowania populacji ofiar i drapieżników)[2].
Podstawowy model
Układ równań zaproponowany przez autorów ma postać:
gdzie:
- x(t) – populacja, czyli liczba ofiar (ang. prey, np. zające),
- y(t) – liczba drapieżców (ang. predators, np. rysie),
- t – rozwój tych dwóch populacji w czasie,
- stałe (a,b,c,d > 0, dodatnie parametry) oznaczają:
- a – częstość narodzin ofiar lub współczynnik przyrostu ofiar,
- b – częstość umierania ofiar na skutek drapieżnictwa,
- c – częstość narodzin drapieżników lub współczynnik przyrostu drapieżników,
- d – częstość umierania drapieżników lub współczynnik ubywania drapieżników,
- y(t) – liczba drapieżców (ang. predators, np. rysie),
Bardzo często do dalszej analizy własności tych równań przeprowadza się ich ubezwymiarowienie za pomocą następujących podstawień:
Powyższe podstawienie prowadzi do następującego układu równań, który zależy już tylko od jednego parametru :
Punkty krytyczne tego układu to oraz Dalsza liniowa analiza prowadzi do wniosku, że punkt jest punktem siodłowym, zaś to centrum stabilne w sensie Lapunowa.
Uogólniony model Lotki-Volterry
Model Lotki-Volterry można uogólnić na większą ilość oddziałujących ze sobą populacji. Wtedy otrzymamy następujący układ równań:
gdzie parametry mają analogiczne znaczenie jak w modelu dwuwymiarowym.
Realistyczny model drapieżnik-ofiara

Główną wadą podstawowego modelu Lotki-Volterry jest fakt, że przy zerowej populacji drapieżników liczebność ofiar wzrasta nieograniczenie. Dlatego też w bardziej realistycznych modelach opisujących to zjawisko wprowadza się chociażby pojemność środowiska – czyli liczbę osobników jaką może maksymalnie osiągnąć dana populacja. Przykładowe równania uwzględniające ten czynnik wyglądają następująco:
gdzie: to nieujemne stałe zależne od modelu.
Często warto zapisać równania w formie bezwymiarowej, by zmniejszyć liczbę parametrów. Powyższe równania skalujemy korzystając z następujących podstawień[3]: będzie ułamkiem pojemności środowiska jaki zajmują ofiary, zaś: określa ułamek pojemności jaki zajmują drapieżnicy a jest przeskalowanym czasem.
Parametry egzogeniczne skalujemy w następujący sposób:
Otrzymujemy wtedy przeskalowane równania Lotki-Volterry w postaci:
Po przyrównaniu prawych stron powyższych równań do zera i ich rozwiązaniu uzyskujemy jeden punkt osobliwy w I ćwiartce. Punkt ten jest stabilny jeśli parametry spełniają:
Jeśli nierówność ta nie zachodzi, to punkt jest niestabilny i z twierdzenia Poincarégo-Bendixsona można wnioskować, że istnieje stabilny cykl graniczny w pierwszej ćwiartce płaszczyzny fazowej[3]. Przestrzeń parametrów jest więc podzielona powierzchnią, pod którą układ dynamiczny realizuje cykl graniczny (więc populacje oscylują w czasie). Nad tą powierzchnią układ posiada jedno nietrywialne rozwiązanie stacjonarne (populację dążą asymptotycznie do stałych wartości).
Modyfikacje modelu Lotki-Volterry
W wyjściowym modelu wpływ na tempo wzrostu populacji mają tylko współczynniki umieralności i narodzin ofiar i drapieżników, podczas gdy w rzeczywistości na proces ten wpływa o wiele więcej czynników, np. konkurencja. Model można zmodyfikować o wpływ konkurencji o pożywienie na tempo wzrostu obu populacji. W efekcie otrzymujemy:
gdzie e i f są współczynnikami konkurencji między osobnikami. Gdy jest dużo drapieżników, konkurują (walczą) między sobą o pożywienie. Natomiast, gdy jest dużo ofiar, maleje ilość pożywienia dla nich.
Innym, równie ważnym, czynnikiem wpływającym na tempo wzrostu obu populacji jest przepełnienie środowiska. Wprowadzając odpowiednie współczynniki, otrzymujemy nowy układ:
gdzie g i h są współczynnikami umieralności związanej z przepełnieniem obszaru, na którym żyją oba gatunki.
Literatura
V. Volterra. Variations and fluctuations of the number of indviduals in animal species living together. In Animal Ecology. McGraw-Hill, 1931. Translated from 1928 edition by R. N. Chapman.
Przypisy
- ↑ J.D. Murray: Wprowadzenie do Biomatematyki. Warszawa: Wydawnictwo Naukowe PWN, 2006. ISBN 83-01-14719-9.
- ↑ Lotki–Volterry równania, [w:] Encyklopedia PWN [online] [dostęp 2021-10-02].
- ↑ a b J.D.Murray: Mathematical Biology, I: An Introduction. York: Springer Publishing, 2002. ISBN 0-387-95223-3.
Linki zewnętrzne
- Eric W. Weisstein, Lotka-Volterra Equations, [w:] MathWorld [online], Wolfram Research [dostęp 2020-12-12] (ang.).
- Symulacja wieloagentowa (pol.) na portalu alife.pl
Media użyte na tej stronie
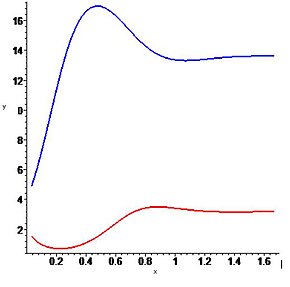
Lotka-Volterra predator-prey time series
Autor: LukashiMiamoto, Licencja: CC0
Wykres przedstawia płaszczyznę która
oddziela przestrzeń fazową parametrów a,b i d. Dla punktów znajdujących się pod płaszczyzną wykresy fazowe dążą do cyklu stabilnego. Dla punktów powyżej płaszczyzny wykresy fazowe
zdążają do ogniska.Autor: LukashiMiamoto, Licencja: CC0
Przykładowy przekrój dla parametru a =
1,4483, gdzie pokazana jest linia oddzielająca domenę z rozwiązaniami stabilnymi od tej niestabilnymi, zwaną krzywą bifurkacyjną. Nad linią punkt przedstawia przykładową kombinację parametrów b i d dla której mamy trajektorię fazową z punktem stabilnym. Pod linią punkt przedstawia przykładową kombinację parametrów b i d dla której mamy trajektorię fazową z punktem
niestabilnym.Zmiany w populacji w zmodyfikowanym modelu Lotki-Volterry (uwzględniającym wewnątrzgatunkową konkurencję o pożywienie)
Autor: User Pokipsy76 on it.wikipedia, Licencja: CC-BY-SA-3.0
Fatto da me con Grafeq, spazio delle fasi delle equazioni di Volterra-Lotka
Autor: LukashiMiamoto, Licencja: CC0
Wykres przedstawia zmiany populacji ofiar i drapieżników w czasie oraz wykres fazowy.