Rozkład Benforda
Rozkład Benforda – rozkład prawdopodobieństwa występowania określonej pierwszej cyfry w wielu rzeczywistych danych statystycznych, np. dotyczących powierzchni jezior, danych z rocznika statystycznego, wartościach stałych fizycznych. Ogólnie rozkład ten sprawdza się w przypadku wielkości, które mogą przyjmować różne rzędy wielkości. Fakt częstego występowania tego rozkładu w obserwowanych danych zwany jest prawem Benforda.
Prawdopodobieństwo wystąpienia cyfry to
Rozkład Benforda jest stosowany do sprawdzania poprawności zeznań podatkowych bądź defraudacji, gdyż ludzie wpisując liczby tak, żeby wydawały się przypadkowe, nie są świadomi, że pewne cyfry występują częściej na pierwszej pozycji.
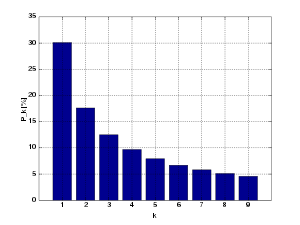
Częstotliwości występowania cyfr na pierwszej pozycji są przedstawione w tabeli poniżej.
| Pierwsza cyfra | Częstość |
|---|---|
| 1 | 30,1% |
| 2 | 17,6% |
| 3 | 12,5% |
| 4 | 9,7% |
| 5 | 7,9% |
| 6 | 6,7% |
| 7 | 5,8% |
| 8 | 5,1% |
| 9 | 4,6% |
Historia
Charakterystyczna zależność została po raz pierwszy odnotowana w 1881 roku przez kanadyjskiego astronoma i matematyka Simona Newcomba. Przebywając w bibliotece United States Naval Observatory, Newcomb zauważył, że strony tablic logarytmicznych są brudniejsze na początku i coraz czystsze na dalszych kartkach. Wywnioskował, że korzystający z tablic logarytmicznych częściej szukają liczb rozpoczynających się od niższych cyfr – te znajdują się na początku tablic. Swoje odkrycie (bez dowodu ogólnej prawidłowości) opublikował na stronach American Journal of Mathematics[1]. Jego artykuł nie spotkał się jednak z szerokim zainteresowaniem i niezwykle ciekawe zjawisko zostało zapomniane na 57 lat.
W 1938 roku Frank Benford, inżynier General Electric, nie zdając sobie sprawy z istnienia pracy Newcomba, dokonał tego samego odkrycia na podstawie stanu czystości tablic logarytmicznych. Zafascynowany tym zjawiskiem, Benford zaczął sprawdzać, czy jego teoria znajduje potwierdzenie również w innych zbiorach danych, m.in. w powierzchniach rzek, liczbach drukowanych w gazetach, czy nawet cenach. Wyniki swoich badań przedstawił w artykule wydrukowanym w Proceedings of the American Philosophical Society[2]. Podobnie jak w artykule Newcomba, formalny dowód nie został przedstawiony.
Dowód twierdzenia podał w 1995 roku Theodore Hill[3].
Przykłady zastosowania
Defraudacja Jamesa Nelsona
Zastosowanie rozkładu Benforda pomogło w wykryciu fałszerstw dokonanych przez Jamesa Nelsona, głównego księgowego i zarządzającego Arizona State Treasurer. W 1992 roku w miasteczku Wayne (Arizona, USA) został uznany za winnego zdefraudowania 1 878 687,58 dolarów. Dokonał tego wystawiając 23 fałszywe czeki.
- oszustwo rozpoczęło się małą kwotą (najmniejszą w całym procederze), przy czym kolejne kwoty fałszywych czeków stopniowo rosły,
- większość czeków wystawiono na kwotę poniżej 100 000 dolarów,
- wykrycie przestępstwa umożliwił rozkład pierwszych cyfr poszczególnych kwot.
Wybory prezydenckie w Iranie 2009
Boudewijn F. Roukema z toruńskiego Uniwersytetu Mikołaja Kopernika zaobserwował, iż rozkład pierwszych cyfr liczby głosów oddanych w wyborach w Iranie w 2009 roku w poszczególnych okręgach na kandydata małej partii opozycyjnej Mehdiego Karroubiego nie zgadza się z rozkładem Benforda – wśród pierwszych cyfr dwukrotnie częściej niż powinna pojawia się siódemka (poziom istotności 0,007). Anomalie występują w trzech z sześciu największych okręgów i są to właśnie okręgi, w których aktualny prezydent Mahmud Ahmadineżad miał proporcjonalnie wyższe poparcie niż w reszcie kraju[4]. Jednakże statystycy Nate Silver[5] i Andrew Gelman[6] wyrazili sceptycyzm w kwestii znaczenia tego wyniku.
Zastosowanie podczas egzaminów
Badacze podejrzewali, że gdy poradzą studentom, aby na teście wielokrotnego wyboru z fizyki sugerowali się rozkładem Benforda, to osiągną oni nieprzeciętnie dobre wyniki. Tak się jednak nie stało, gdyż okazało się, że niepoprawne odpowiedzi również spełniają rozkład Benforda. Naukowcy nie wiedzą, dlaczego[7].
Fizyka kwantowa
Rozkład Benforda częściej daje poprawne wyniki zachowania przejść fazowych w kwantowych modelach XY niż inne teorie (wykorzystują one magnetyzację, splątanie kwantowe czy kwantową niezgodę („quantum discord”)[8].
Zobacz też
Przypisy
- ↑ Simon Newcomb. Note on the frequency of use of the different digits in natural numbers. „Statistical Science”. 78, s. 551–572, 1938. Proceedings of the American Philosophical Society (ang.).
- ↑ Frank Benford. The law of anomalous numbers. „Statistical Science”. 10, s. 354-363, 1995. Institute of Mathematical Statistics. JSTOR: 984802 (ang.).
- ↑ Hill Theodore. A Statistical Derivation of the Significant-Digit Law. „Statistical Science”. 10, s. 354-363, 1995. Institute of Mathematical Statistics (ang.).
- ↑ Boudewijn F. Roukema, A first-digit anomaly in the 2009 Iranian presidential election, „Journal of Applied Statistics”, 41 (1), 2014, DOI: 10.1080/02664763.2013.838664, arXiv:0906.2789 [stat.AP] (ang.).
- ↑ Nate Silver. Statistical Report Purporting to Show Rigged Iranian Election Is Flawed. „fivethirtyeight.com”, 13 czerwca 2009. (kopia w Archiwum Internetu); Nate Silver. Karroubi's Unlucky 7's?. „fivethirtyeight.com”, 18 czerwca 2009. (kopia w Archiwum Internetu)
- ↑ Andrew Gelman. Unconvincing (to me) Use of Benford's Law to Demonstrate Election Fraud in Iran. „fivethirtyeight.com”, 18 czerwca, 2009. (kopia w Archiwum Internetu)
- ↑ Researchers apply Benford's law to physics exams to see if they can do better than chance, phys.org [dostęp 2017-11-26] (ang.).
- ↑ Ameya Deepak Rane i inni, Benford's law gives better scale exponents in phase transitions of quantum XY models, „Physical Review E & arXiv [quant-ph]”, 90 (2), 2014, s. 022144, DOI: 10.1103/PhysRevE.90.022144, arXiv:1405.2744 (ang.).
Bibliografia
Media użyte na tej stronie
Rozkład Benforda
A narrow probability distribution plotted on a log scale, to demonstrate a case where Benford's law does not hold. This is to be contrasted with BenfordBroad.gif.
A broad probability distribution on a log scale, with bars colored in to show why Benford's law holds