Rozkład Studenta

Rozkład Studenta, rozkład t Studenta

Gęstość prawdopodobieństwa
Dystrybuanta
Parametry	${\displaystyle \nu >0}$ stopni swobody (liczba rzeczywista)
Nośnik	${\displaystyle x\in (-\infty ;+\infty )}$
Gęstość prawdopodobieństwa	${\displaystyle {\frac {\Gamma ({\frac {\nu +1}{2}})}{{\sqrt {\nu \pi }}\,\Gamma ({\frac {\nu }{2}})}}\left(1+{\frac {x^{2}}{\nu }}\right)^{-({\frac {\nu +1}{2}})}}$
Dystrybuanta	${\displaystyle {\begin{matrix}{\frac {1}{2}}+x\Gamma \left({\frac {\nu +1}{2}}\right)\cdot \\[0.5em]{\frac {\,_{2}F_{1}\left({\frac {1}{2}},{\frac {\nu +1}{2}};{\frac {3}{2}};-{\frac {x^{2}}{\nu }}\right)}{{\sqrt {\pi \nu }}\,\Gamma ({\frac {\nu }{2}})}}\end{matrix}}}$ gdzie ${\displaystyle _{2}F_{1}}$ jest funkcją hipergeometryczną
Wartość oczekiwana (średnia)	${\displaystyle 0{\text{ dla }}\nu >1,}$ w przeciwnym wypadku nieokreślona
Mediana	${\displaystyle 0}$
Moda	${\displaystyle 0}$
Wariancja	${\displaystyle {\frac {\nu }{\nu -2}}{\text{ dla }}\nu >2,}$ w przeciwnym wypadku nieokreślona
Współczynnik skośności	${\displaystyle 0{\text{ dla }}\nu >3}$
Kurtoza	${\displaystyle {\frac {6}{\nu -4}}{\text{ dla }}\nu >4}$
Entropia	${\displaystyle {\begin{matrix}{\frac {\nu +1}{2}}\left[\psi ({\frac {1+\nu }{2}})-\psi ({\frac {\nu }{2}})\right]\\[0.5em]+\ln {\left[{\sqrt {\nu }}B({\frac {\nu }{2}},{\frac {1}{2}})\right]}\end{matrix}}}$ ${\displaystyle \psi {:}}$ funkcja digamma ${\displaystyle B{:}}$ funkcja beta
Funkcja tworząca momenty	(nieokreślona)
Odkrywca	William Sealy Gosset (1908)

Rozkład Studenta, rozkład t Studenta, rozkład t – ciągły rozkład prawdopodobieństwa stosowany często w statystyce w procedurach testowania hipotez statystycznych i przy ocenie niepewności pomiaru. Przy opracowaniu wyników pomiarów często powstaje zagadnienie oszacowania przedziału, w którym leży, z określonym prawdopodobieństwem, rzeczywista wartość mierzona, jeśli dysponujemy tylko wynikami n pomiarów, dla których możemy wyznaczyć takie parametry, jak średnia ${\displaystyle {\overline {X}}}$ i odchylenie standardowe ${\displaystyle s}$ lub wariancja ${\displaystyle s^{2}}$ („z próby”), nie znamy natomiast odchylenia standardowego ${\displaystyle \sigma }$ w populacji. Zagadnienie to rozwiązał w 1908 r. William Sealy Gosset (pseudonim Student) podając funkcję zależną od wyników pomiarów ${\displaystyle X_{i},}$ a niezależną od ${\displaystyle \sigma .}$

Definicja

Rozkład Studenta z ${\displaystyle n}$ stopniami swobody jest rozkładem zmiennej losowej ${\displaystyle T}$ postaci:

${\displaystyle T={\frac {U}{\sqrt {Z}}}{\sqrt {n}}}$

gdzie:

• ${\displaystyle U}$ jest zmienną losową mającą standardowy rozkład normalny ${\displaystyle N(0,1)}$
• ${\displaystyle Z}$ jest zmienną losową o rozkładzie chi kwadrat o ${\displaystyle n}$ stopniach swobody
• ${\displaystyle U}$ i ${\displaystyle Z}$ są niezależne.

Gęstość prawdopodobieństwa

Zmienna losowa ${\displaystyle T}$ określona powyżej ma gęstość prawdopodobieństwa opisaną wzorem:

${\displaystyle f(t,n)={\frac {\Gamma ({\frac {n+1}{2}})}{\Gamma ({\frac {n}{2}}){\sqrt {n\pi }}}}\left(1+{\frac {t^{2}}{n}}\right)^{-{\frac {n+1}{2}}}}$

gdzie ${\displaystyle \Gamma (x)}$ to funkcja gamma.

Dowód. Niech ${\displaystyle U}$ i ${\displaystyle Z}$ będą takie jak wyżej. Zmienna ${\displaystyle Y={\sqrt {Z}}}$ ma rozkład chi o ${\displaystyle n}$ stopniach swobody, a więc gęstość ${\displaystyle Y}$ wyraża się wzorem

${\displaystyle f_{Y}(y)={\frac {2^{1-{\frac {n}{2}}}y^{n-1}e^{-{\frac {y^{2}}{2}}}}{\Gamma ({\frac {n}{2}})}}.}$

Rozważmy zmienną

${\displaystyle X={\frac {1}{\sqrt {n}}}Y.}$

Wówczas

${\displaystyle {\frac {\partial Y}{\partial X}}={\sqrt {n}}}$

a zatem całkując przez podstawienie obserwujemy, że

${\displaystyle {\begin{aligned}f_{X}(x)&=f_{Y}({\sqrt {n}}x){\Big |}{\frac {\partial Y}{\partial X}}{\Big |}\\&={\frac {2^{1-{\frac {n}{2}}}}{\Gamma \left({\frac {n}{2}}\right)}}({\sqrt {n}}x)^{n-1}e^{-{\frac {({\sqrt {n}}x)^{2}}{2}}}{\sqrt {n}}\\&={\frac {2^{1-{\frac {n}{2}}}}{\Gamma \left({\frac {n}{2}}\right)}}n^{\frac {n}{2}}x^{n-1}e^{-{\frac {n}{2}}x^{2}}.\end{aligned}}}$

Zmienna ${\displaystyle T}$ ma zatem rozkład ${\displaystyle U/X.}$ Jej gęstość jest więc postaci

${\displaystyle {\begin{aligned}f_{T}(t)&=\int \limits _{-\infty }^{\infty }|x|f_{U}(xt)f_{X}(x)\,\mathrm {d} x=\int \limits _{0}^{\infty }xf_{U}(xt)f_{X}(x)\,\mathrm {d} x\\&=\int \limits _{0}^{\infty }x{\frac {1}{\sqrt {2\pi }}}e^{-{\frac {(xt)^{2}}{2}}}{\frac {2^{1-{\frac {n}{2}}}}{\Gamma \left({\frac {n}{2}}\right)}}n^{\frac {n}{2}}x^{n-1}e^{-{\frac {n}{2}}x^{2}}\,\mathrm {d} x\\&={\frac {n^{\frac {n}{2}}}{\sqrt {2\pi }}}{\frac {2^{1-{\frac {n}{2}}}}{\Gamma \left({\frac {n}{2}}\right)}}\int \limits _{0}^{\infty }x^{n}e^{-{\frac {1}{2}}(n+t^{2})x^{2}}\,\mathrm {d} x.\end{aligned}}}$

Niech ${\displaystyle m=x^{2}.}$ Wówczas powyższa całka przyjmuje postać

${\displaystyle \int \limits _{0}^{\infty }x^{n}e^{-{\frac {1}{2}}(n+t^{2})m}{\frac {\mathrm {d} m}{2x}}={\frac {1}{2}}\int \limits _{0}^{\infty }m^{\frac {n-1}{2}}e^{-{\frac {1}{2}}(n+t^{2})m}\mathrm {d} m\qquad (*).}$

Gęstość ${\displaystyle f(m;k,\theta )}$ rozkładu gamma wyraża się wzorem

${\displaystyle f(m;k,\theta )={\frac {m^{k-1}e^{-{\frac {m}{\theta }}}}{\theta ^{k}\Gamma (k)}}.}$

Oznacza to, że

${\displaystyle k-1={\frac {n-1}{2}}\Rightarrow k^{*}={\frac {n+1}{2}},\qquad {\frac {1}{\theta }}={\frac {1}{2}}(n+t^{2})\Rightarrow \theta ^{*}={\frac {2}{(n+t^{2})}}}$

a stąd

${\displaystyle (*)={\frac {1}{2}}(\theta ^{*})^{k^{*}}\Gamma (k^{*})={\frac {1}{2}}{\Big (}{\frac {2}{n+t^{2}}}{\Big )}^{\frac {n+1}{2}}\Gamma \left({\frac {n+1}{2}}\right)=2^{\frac {n-1}{2}}n^{-{\frac {n+1}{2}}}\Gamma \left({\frac {n+1}{2}}\right)\left(1+{\frac {t^{2}}{n}}\right)^{-{\frac {1}{2}}(n+1)}.}$

Ostatecznie

${\displaystyle f_{T}(t)={\frac {1}{\sqrt {2\pi }}}{\frac {2^{1-{\frac {n}{2}}}}{\Gamma \left({\frac {n}{2}}\right)}}n^{\frac {n}{2}}2^{\frac {n-1}{2}}n^{-{\frac {n+1}{2}}}\Gamma \left({\frac {n+1}{2}}\right)\left(1+{\frac {t^{2}}{n}}\right)^{-{\frac {1}{2}}(n+1)}={\frac {\Gamma [(n+1)/2]}{{\sqrt {n\pi }}\Gamma (n/2)}}\left(1+{\frac {t^{2}}{n}}\right)^{-{\frac {1}{2}}(n+1)}.}$

Własności

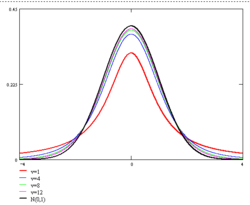
Powyższy wzór określa całą rodzinę rozkładów prawdopodobieństwa zależną od parametru ${\displaystyle n}$ – liczby stopni swobody rozkładu Studenta. Rozkłady te są symetryczne, jednomodalne, dla dużych wartości ${\displaystyle n}$ zmierzają do standardowego rozkładu normalnego ${\displaystyle N(0,1).}$ Dla małych ${\displaystyle n}$ różnią się jednak od rozkładu normalnego: rozkład Studenta o ${\displaystyle n}$ stopniach swobody ma skończone momenty tylko do rzędu ${\displaystyle n-1,}$ w szczególności dla ${\displaystyle n=1}$ rozkład Studenta jest identyczny z rozkładem Cauchy’ego i nie posiada żadnych skończonych momentów (nie istnieje nawet wartość średnia).

Własności te ilustruje poniższy wykres przedstawiający gęstości rozkładu Studenta dla kilku wartości liczby stopni swobody ${\displaystyle n}$ w zestawieniu z gęstością standardowego rozkładu normalnego ${\displaystyle N(0,1).}$

Zastosowania

Zastosowania rozkładu Studenta w metrologii i statystyce opierają się w większości na następujących dwóch twierdzeniach:

1. Niech zmienne losowe ${\displaystyle X_{1},X_{2},...,X_{n}}$ mają jednakowy rozkład prawdopodobieństwa, który jest rozkładem normalnym o średniej ${\displaystyle m}$ i wariancji ${\displaystyle \sigma ^{2}}$ oraz niech zmienna ${\displaystyle t}$ będzie określona wzorem:

   ${\displaystyle t={\frac {{\overline {X}}-m}{s}}\cdot {\sqrt {n}}}$

   gdzie ${\displaystyle {\overline {X}}}$ jest wartością średnią z próby, zaś ${\displaystyle s}$ – odchyleniem standardowym z próby.

   Wówczas zmienna ${\displaystyle t}$ ma rozkład Studenta o ${\displaystyle \nu =n-1}$ stopniach swobody (niezależny od wartości wariancji w populacji ${\displaystyle \sigma ^{2}}$).

2. Jeżeli dwie próby o liczebnościach ${\displaystyle n_{1}}$ oraz ${\displaystyle n_{2},}$ wartościach średnich ${\displaystyle {\overline {X}}_{1}}$ oraz ${\displaystyle {\overline {X}}_{2}}$ i wariancjach wyznaczonych z próby ${\displaystyle s_{1}^{2}}$ oraz ${\displaystyle s_{2}^{2}}$ zostały wylosowane z populacji mających taki sam rozkład normalny, to zmienna ${\displaystyle t}$ określona wzorem:

   ${\displaystyle t={\frac {{\overline {X}}_{1}-{\overline {X}}_{2}}{\sqrt {n_{1}s_{1}^{2}+n_{2}s_{2}^{2}}}}{\sqrt {{\frac {n_{1}n_{2}}{n_{1}+n_{2}}}(n_{1}+n_{2}-2)}}}$

   ma rozkład Studenta o ${\displaystyle \nu =n_{1}+n_{2}-2}$ stopniach swobody.

Rozkład t jest stosowany w estymacji przedziałowej, w testach parametrycznych, w szczególności dla wartości średnich i dla wariancji oraz w testach istotności parametrów statystycznych – gdy mamy do czynienia z próbami małymi (najczęściej arbitralnie przyjmuje się, że próba jest mała gdy jej liczebność ${\displaystyle n\leqslant 30}$).

W metrologii rozkład Studenta wykorzystywany jest m.in. przy estymacji odchylenia standardowego (dla pojedynczego pomiaru oraz wartości oczekiwanej). Dla dużych prób (n > 30) praktycznie pokrywa się z rozkładem normalnym, dla mniejszych estymator odchylenia należy pomnożyć przez wartość krytyczną rozkładu Studenta dla liczby stopni swobody ${\displaystyle \nu =n-1}$ i przyjętego poziomu istotności ${\displaystyle \alpha .}$

Najczęściej potrzebne są w zastosowaniach kwantyle rozkładu Studenta, to znaczy takie wartości ${\displaystyle t_{\alpha },}$ że ${\displaystyle P(t>t_{\alpha })=\alpha }$ lub ${\displaystyle P(|t|<t_{\alpha })=\alpha .}$ Wartości te podają tablice rozkładu Studenta.

Bibliografia

• Zieliński R., Tablice statystyczne, PWN, Warszawa 1972.

Linki zewnętrzne

• VassarStats. vassarstats.net. [zarchiwizowane z tego adresu (2016-03-04)]. Wykresy gęstości, wartości krytyczne i in. obliczane dla podanej przez użytkownika liczby stopni swobody.
• Earliest Known Uses of Some of the Words of Mathematics (S). [dostęp 2009-05-27]. (ang.). (O historii terminu „Rozkład Studenta”)
• Distribution Calculator Kalkulator obliczający prawdopodobieństwa i wartości krytyczne dla rozkładu normalnego, Studenta, chi-kwadrat oraz F
• Kalkulator rozkładu – polski kalkulator online szacujący wartość statystyki t Studenta dla zadanej liczby stopni swobody
• Tablice podstawowych rozkładów rachunku prawdopodobieństwa