Rzut (algebra liniowa)

Rzut lub projekcja^[a] – uogólnienie pojęcia rzutu znanego z geometrii elementarnej: idempotentny endomorfizm liniowy określony na danej przestrzeni liniowej, czyli operator liniowy zachowujący swój obraz, tzn. dla którego każdy element obrazu jest punktem stałym tego przekształcenia.

Rzuty/projekcje ortogonalne są uogólnieniem pojęcia rzutu prostokątnego z geometrii euklidesowej (zob. osobna sekcja); w przestrzeniach unitarnych (tzn. z iloczynem skalarnym, np. przestrzeniach euklidesowych) są to ni mniej, ni więcej operatory samosprzężone.

Rzut ukośny

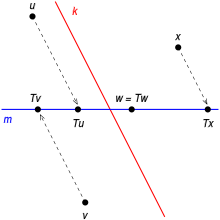
Rzut ${\displaystyle \mathrm {T} }$ wzdłuż prostej ${\displaystyle k}$ na prostą ${\displaystyle m.}$

Niech dana będzie przestrzeń liniowa ${\displaystyle V}$ (nad ustalonym ciałem). Przekształcenie liniowe ${\displaystyle \mathrm {P} \colon V\to V}$ tej przestrzeni w siebie spełniające warunek idempotentności

${\displaystyle \mathrm {P} ^{2}=\mathrm {P} ,}$

czyli ${\displaystyle \mathrm {P} {\big (}\mathrm {P} (\mathbf {v} ){\big )}=\mathrm {P} (\mathbf {v} )}$ dla każdego ${\displaystyle \mathbf {v} \in V}$ nazywa się rzutem (ukośnym) lub projekcją.

Odwzorowanie ${\displaystyle \mathrm {P} }$ można scharakteryzować w następujący sposób: dowolny wektor ${\displaystyle \mathbf {v} \in V}$ można przedstawić w jednoznaczny sposób w postaci sumy ${\displaystyle \mathbf {v} =\mathbf {w} +\mathbf {u} ,}$ gdzie ${\displaystyle \mathbf {w} \in \ker \mathrm {P} }$ oraz ${\displaystyle \mathbf {u} \in \mathrm {im\;P} }$^[b]. Oznacza to, że ${\displaystyle V=\ker \mathrm {P} \oplus \mathrm {im\;P} ,}$ czyli ${\displaystyle V}$ jest sumą prostą jądra i obrazu ${\displaystyle \mathrm {P} .}$ Jeżeli ${\displaystyle V}$ jest skończeniewymiarowa, zaś ${\displaystyle U}$ jest jej podprzestrzenią liniową, to na mocy twierdzenia o rzędzie istnieje rzut ${\displaystyle \mathrm {P} ,}$ dla którego ${\displaystyle \mathrm {im\;P} =U}$ (jeśli ${\displaystyle 0<\dim U<\dim V,}$ to rzutów określonych na ${\displaystyle V}$ o obrazie ${\displaystyle U}$ jest nieskończenie wiele).

Dla danych podprzestrzeni ${\displaystyle W,U}$ przestrzeni ${\displaystyle V}$ spełniających ${\displaystyle V=W\oplus U}$ przekształcenie ${\displaystyle \mathrm {P} \colon V\to V}$ nazywa się rzutem na ${\displaystyle U}$ wzdłuż ${\displaystyle W,}$ jeśli dla każdego ${\displaystyle \mathbf {v} \in V}$ zachodzi

${\displaystyle \mathrm {P} (\mathbf {v} )\in U}$ oraz ${\displaystyle \mathbf {v} -\mathrm {P} (\mathbf {v} )\in W.}$

Jedynymi wartościami własnymi rzutu są zero i jedynka, tzn. widmo rzutu ${\displaystyle \mathrm {P} }$ jest równe ${\displaystyle \sigma (\mathrm {P} )=\{0,1\}}$^[c]; ponadto rzut jest diagonalizowalny i w szczególności (w ciele charakterystyki zerowej) jego ślad jest równy wymiarowi obrazu^[d]. Z drugiej strony, jeśli przekształcenie ${\displaystyle \mathrm {A} }$ ma widmo ${\displaystyle \sigma (\mathrm {A} )=\{0,1\}}$ i jest diagonalizowalne, to ${\displaystyle \mathrm {A} }$ jest rzutem^[e].

Jeśli ${\displaystyle \mathrm {P} }$ jest rzutem na ${\displaystyle U}$ wzdłuż ${\displaystyle W,}$ to przekształcenie ${\displaystyle \mathrm {Q} =\mathrm {I} -\mathrm {P} \colon V\to V}$ dane wzorem ${\displaystyle \mathrm {Q} (\mathbf {v} )=\mathbf {v} -\mathrm {P} (\mathbf {v} )}$ jest rzutem na ${\displaystyle W}$ wzdłuż ${\displaystyle U}$^[f]. Tym samym rozkładowi ${\displaystyle V=U\oplus W}$ odpowiada para rzutów ${\displaystyle \mathrm {P} ,\mathrm {Q} .}$

Rzut ortogonalny

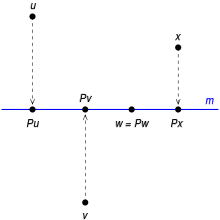
Rzut ortogonalny ${\displaystyle \mathrm {P} }$ na prostą ${\displaystyle m.}$

Jeżeli ${\displaystyle \mathrm {P} }$ jest rzutem (ukośnym) na ${\displaystyle U}$ wzdłuż ${\displaystyle W}$ oraz ${\displaystyle V=W\perp U}$ jest ortogonalną sumą prostą, to ${\displaystyle \mathrm {P} }$ nazywa się rzutem ortogonalnym (na ${\displaystyle U}$ wzdłuż ${\displaystyle W}$). Wówczas ${\displaystyle W=U^{\perp }}$ jest dopełnieniem ortogonalnym ${\displaystyle U,}$ czyli zachodzi ${\displaystyle V=U^{\perp }\oplus U,}$ a więc ${\displaystyle V=(\mathrm {im\;P} )^{\perp }\oplus \mathrm {im\;P} ,}$ gdyż wtedy ${\displaystyle \ker P=(\mathrm {im\;P} )^{\perp },}$ gdzie ${\displaystyle \mathrm {im\;P} }$ oraz ${\displaystyle \ker \mathrm {P} }$ oznaczają odpowiednio obraz i jądro rzutu ${\displaystyle \mathrm {P} .}$

Konstrukcja ortogonalnej sumy prostej wymaga istnienia (niezdegenerowanej) symetrycznej formy dwuliniowej określonej na przestrzeni (tzw. przestrzeń ortogonalna): zwykle rozważa się przestrzenie z iloczynem skalarnym (tzw. przestrzenie unitarne); w przypadku przestrzeni nieskończonego wymiaru zakłada się dodatkowo zupełność, co sprawia, że przestrzeń unitarna ${\displaystyle V}$ staje się przestrzenią Hilberta – istnienie zapewnia wtedy twierdzenie o rzucie ortogonalnym. W tym kontekście rzut ukośny nazywa się operatorem idempotentnym, a rzut ortogonalny znany jest jako operator rzutowy.

Rzut jest ortogonalny wtedy i tylko wtedy, gdy jest i) samosprzężony^[g] lub ii) normalny lub iii) dodatni (dodatnio określony) lub iv) izometryczny. Rzuty ortogonalne są operatorami ograniczonymi (czyli ciągłymi), a gdy są nietrywialne: o jednostkowej normie operatorowej^[h]; z drugiej strony ograniczony (równoważnie: ciągły) operator liniowy ${\displaystyle \mathrm {A} }$ na przestrzeni Hilberta jest rzutem ortogonalnym wtedy i tylko wtedy, gdy ${\displaystyle \mathrm {A} ^{*}\mathrm {A} =\mathrm {A} .}$

Gdy rozważana przestrzeń jest zespolona, gwiazdkę przy oznaczeniu macierzy należy interpretować jako sprzężenie hermitowskie, w pozostałych przypadkach – jako transpozycję; w przypadku przekształceń gwiazdka oznacza (antyliniowe) przekształcenie sprzężone do danego.

Jeśli ${\displaystyle \mathbf {u} _{1},\dots ,\mathbf {u} _{k}}$ jest bazą ortonormalną podprzestrzeni ${\displaystyle U}$ zaś ${\displaystyle \mathbf {A} }$ oznacza macierz typu ${\displaystyle n\times k,}$ której kolumnami są ${\displaystyle \mathbf {u} _{1},\dots ,\mathbf {u} _{k},}$ to macierz rzutu ortogonalnego dana jest wzorem

${\displaystyle \mathbf {P} _{\mathbf {A} }=\mathbf {AA} ^{*}}$

i reprezentuje ona przekształcenie, które można zapisać jako^[i]

${\displaystyle \mathrm {P} _{\mathrm {A} }(\cdot )=\sum _{i=1}^{k}\mathbf {u} _{i}\langle \mathbf {u} _{i},\cdot \rangle .}$

W szczególności rzut na prostą (przestrzeń jednowymiarową) rozpinaną przez wektor jednostkowy ${\displaystyle \mathbf {u} }$ dany jest wzorem ${\displaystyle \mathrm {P} _{\mathbf {u} }(\cdot )=\mathbf {u} \langle \mathbf {u} ,\cdot \rangle ,}$ a jego macierz ma postać ${\displaystyle \mathbf {P} _{\mathbf {u} }=\mathbf {uu} ^{*}}$^[j].

Macierz ${\displaystyle \mathbf {A} ^{*}}$ reprezentuje izometrię częściową ${\displaystyle \mathrm {A} ^{*},}$ która znika na dopełnieniu ortogonalnym podprzestrzeni ${\displaystyle U,}$ zaś ${\displaystyle \mathrm {A} }$ jest izometrią, która zanurza ${\displaystyle U}$ w przestrzeń ${\displaystyle V.}$

Warunek ortonormalności można opuścić; jeżeli ${\displaystyle \mathbf {u} _{1},\dots ,\mathbf {u} _{k}}$ jest bazą (niekoniecznie ortonormalną), a macierz ${\displaystyle \mathbf {A} }$ zawiera te wektory jako kolumny, to rzut ma postać^[k]

${\displaystyle \mathbf {P} _{\mathbf {A} }=\mathbf {A} (\mathbf {A} ^{*}\mathbf {A} )^{-1}\mathbf {A} ^{*}.}$

Reprezentowane przez tę macierz przekształcenie nadal zanurza ${\displaystyle U}$ w przestrzeń ${\displaystyle V,}$ jednak nie musi być już izometrią.

Przykłady

• Przekształcenie tożsamościowe jest rzutem ortogonalnym reprezentowanym przez macierz jednostkową, np. ${\displaystyle \left[{\begin{smallmatrix}1&0\\0&1\end{smallmatrix}}\right]}$ (operator jednostkowy jest operatorem rzutowym).

• Przekształcenie liniowe, którego macierz ma postać ${\displaystyle \left[{\begin{smallmatrix}1&0\\0&0\end{smallmatrix}}\right],}$ jest rzutem ortogonalnym, podczas gdy zadane macierzą ${\displaystyle \left[{\begin{smallmatrix}0&1\\0&1\end{smallmatrix}}\right]}$ jest rzutem (ukośnym), ale nie ortogonalnym (pierwsza macierz opisuje operator rzutowy, druga – tylko idempotentny).

• Przestrzeń ${\displaystyle \mathrm {L} ^{2}(\mathbb {R} )}$ funkcji rzeczywistych całkowalnych z kwadratem (w sensie Lebesgue’a) jest ortogonalną sumą prostą przestrzeni ${\displaystyle M,N}$ funkcji parzystych i nieparzystych; rzuty ${\displaystyle \mathrm {P} _{M},\mathrm {P} _{N}}$ odpowiednio na ${\displaystyle M,N}$ dane są wzorami^[l]

  ${\displaystyle \mathrm {P} _{M}f(x)={\tfrac {f(x)+f(-x)}{2}}\qquad {\text{ oraz }}\qquad \mathrm {P} _{N}f(x)={\tfrac {f(x)-f(-x)}{2}},}$

przy czym ${\displaystyle \mathrm {I} -\mathrm {P} _{M}=\mathrm {P} _{N}.}$

• Niech ${\displaystyle A}$ będzie zbiorem mierzalnym ${\displaystyle \mathbb {R} ,}$ np. przedziałem, z funkcją charakterystyczną ${\displaystyle \chi _{A}.}$ Wówczas^[l] ${\displaystyle \mathrm {P} _{A}f(x)=\chi _{A}(x)f(x)}$ jest rzutem ortogonalnym ${\displaystyle \mathrm {L} ^{2}(\mathbb {R} )}$ na podprzestrzeń funkcji o nośniku zawartym w domknięciu ${\displaystyle {\overline {A}}.}$

• Zamiast wspomnianej wcześniej przestrzeni Hilberta ${\displaystyle \mathbb {R} ^{n}}$ z operatorem ${\displaystyle \mathrm {P} _{\mathbf {u} }(\mathbf {x} )=\mathbf {uu} ^{*}\mathbf {x} }$ można rozważać inne: w przypadku przestrzeni ciągów ${\displaystyle \ell ^{2}(\mathbb {Z} ),}$ gdy ${\displaystyle \mathbf {u} =\mathbf {e} _{n},}$ gdzie ${\displaystyle \mathbf {e} _{n}=\left(\delta _{k,n}\right)_{k=-\infty }^{+\infty }}$^[m], oraz ${\displaystyle \mathbf {x} =(x_{k}),}$ to rzut przyjmuje postać ${\displaystyle \mathrm {P} _{\mathbf {e} _{n}}(\mathbf {x} )=x_{n}\mathbf {e} _{n}.}$

• Jeśli z kolei dana jest przestrzeń ${\displaystyle \mathrm {L} ^{2}(\mathbb {T} )}$ jest przestrzenią funkcji o okresie ${\displaystyle 2\pi }$^[n], a ${\displaystyle u=1/{\sqrt {2\pi }}}$ jest funkcją stałą o jednostkowej normie, to rzut ortogonalny ${\displaystyle \mathrm {P} _{u}}$ przekształca funkcję ${\displaystyle f}$ w jej średnią ${\displaystyle \langle f\rangle ,}$ gdzie

  ${\displaystyle \langle f\rangle ={\frac {1}{2\pi }}\int _{0}^{2\pi }\!\!f(x)\ \mathrm {d} x.}$

Odpowiadający temu rzutowi rozkład ortogonalny, ${\displaystyle f(x)=\langle f\rangle +f'(x),}$ rozbija funkcję na stałą część średnią ${\displaystyle \langle f\rangle }$ i zmienną część ${\displaystyle f'}$ o zerowej średniej.

• Stosowany w matematycznym opisie mechaniki kwantowej operator liczby cząstek dla fermionów jest operatorem rzutowym.

Uwagi

Bibliografia

• F.W. Gehring, P.R. Halmos, C.C Moore: A Course in Functional Analysis. Nowy Jork: Springer-Verlag, 1985.