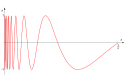
Sinusoida zagęszczona

Sinusoida zagęszczona

Sinusoida zagęszczona albo warszawska – krzywa na płaszczyźnie stosowana czasem jako przykład w topologii. W zwykłym położeniu definiuje się ją jako zbiór będący sumą wykresu funkcji ${\displaystyle y=\sin {\tfrac {1}{x}},0<x\leqslant {\tfrac {1}{\pi }}}$ i odcinka ${\displaystyle \{(0,y):-1\leqslant y\leqslant 1\}.}$

W topologii każdą przestrzeń topologiczną, która jest homeomorficzna z tak zdefiniowaną sinusoidą zagęszczoną nazywa się również sinusoidą zagęszczoną. Wymiar tej przestrzeni jest równy 1.

Sinusoida zagęszczona jest przykładem continuum, zatem przestrzeni spójnej, które jednak nie jest lokalnie spójne i nie jest łukowo spójne.

Bibliografia

• JerzyJ. Mioduszewski JerzyJ., Wykłady z topologii. Topologia przestrzeni euklidesowych, Katowice: Wydawnictwo Uniwersytetu Śląskiego, 1994, ISSN 0239-6432 .